Percent Difference – Explanation & Examples

The percent difference is the difference between two numbers expressed in percentage. To understand the concept of a percent difference, we must first understand what is meant by a percentage? A percentage is a number that is expressed as a fraction of 100.

For example, $10$ percent or $10\%$ means $\dfrac{10}{100}$. We can also use it to describe a relation between two numbers. For example, $24$ is $20\%$ of $120$. The percentage sign is denoted by “%” and is equal to $\dfrac{1}{100}$. Say we want to calculate $8\%$ of $150$, we simply do the following calculations.

                                                       $8\%\hspace{1mm} of \hspace{1mm} 150 = [\dfrac{8}{100}] \times 150 = 12$.

The percent difference is the ratio of the absolute difference of two values and their average value, multiplied by 100.

You should refresh the following concepts to understand the material discussed here.

1. Percentage.
2. Basic Arithmetic.

What is Percent Difference

The percent difference is used to calculate the difference between two non-identical positive numbers, and it is expressed in percentage. For example, we have two numbers, $26$ and $10$; we want to calculate the percent difference between these two numbers.

The first step is to calculate the difference between them; in this case that would be $26\hspace{1mm} –\hspace{1mm} 10 = 16$ or $10\hspace{1mm} – \hspace{1mm}26 = -16$. We are not provided with the information on which number is original or which number is the new one; we are simply given two numbers and have to calculate the difference between them.

So, in this example, the difference is $16$ or $-16$. Still, as we are using the absolute value in the calculation of percent difference, so the result will always be a positive number.

Hence, the difference is 16 no matter which number we take as “a” and which number as “b.” Once we calculate the difference, now it is time to decide the reference or base value that we can use for divis. As we just mentioned, we have not been given any data regarding the context of the two numbers, so taking the average of the two numbers is a good solution.

The average value in this example is calculated as $\dfrac {(26\hspace{1mm}+\hspace{1mm}10)}{2}= 18$. We will calculate the percent difference by dividing the number $16$ by average value $18$ and then multiplying by $100$, and the result will be $88.88 \%$.

Percentage Difference = [Absolute difference of the two numbers/Average of those numbers] * 100.

How to Calculate Percent Difference

Calculation of the percent difference is pretty simple and easy. But, first, you need to follow the steps given below.

1. Name the two given numbers as “a” and “b.”
2. Calculate the absolute difference between the given two numbers: $|a\hspace{1mm} -\hspace{1mm} b|$
3. Calculate the average of the two numbers by using the following formula: $\dfrac{(a\hspace{1mm}+\hspace{1mm} b)} { 2}$.
4. Now divide the value calculated in step 2 with the average value calculated in step 3: $\dfrac{ |a\hspace{1mm}-\hspace{1mm} b|} { ((a\hspace{1mm} +\hspace{1mm} b) / 2)}$.
5. Express the final answer in percentage by multiplying the result in step 4 by $100$

Percent Difference Formula:

We can calculate the percent difference by using the formula given below.

$\mathbf{Percentage\hspace{1mm} Difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)\hspace{1mm}/2}]\times 100}$

Here,

a and b  = Two non-identical positive numbers.

$| a\hspace{1mm} -\hspace{1mm} b |$ = Absolute difference value of two numbers

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2}$ = Average of two numbers

Example 1:  Calculate the Percent difference between number $30$ and $15$.

Solution:

Let $ a = 30$ and $b =15$

$a\hspace{1mm}-\hspace{1mm}b = 30 \hspace{1mm}-\hspace{1mm}15 = 15$

$| a\hspace{1mm} -\hspace{1mm} b |= | 15 | = 15$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \frac{30\hspace{1mm} +\hspace{1mm} 15}{2} = \frac{45}{2} = 22.5$

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)/2}]\times 100$

$Percent\hspace{1mm} difference = [\dfrac{\left | 15 \right |}{22.5}]\times 100$

$Percent \hspace{1mm}difference = 0.666\times 100 = 66.7\%$

Percent Difference vs. Percent Change:

A related concept to percent difference is percent change, and it is very easy to confuse the two. In this section, we will clear the difference between these two concepts.

The formula for percentage difference is given as.

$\mathbf{Percentage\hspace{2mm} Difference = [\dfrac{\left | a-b \right |}{(a+b)/2}]\times 100 }$

The formula for percentage change is given as.

$\mathbf{Percentage\hspace{2mm} Change = [\dfrac{x2 -x1}{\left | x1 \right |}]\times 100 }$

Here,

x1  = Initial value.

x2  = Final value.

| x1 |= Absolute Initial Value

For example, you are given two numbers. The initial number is = 30, and the final number is = 20, and you are required to calculate the percent difference between these two numbers.

Let $a = 30$ and $b =20$

$a\hspace{1mm}-\hspace{1mm}b = 30 \hspace{1mm}-\hspace{1mm} 20 = 10$

$| a\hspace{1mm} -\hspace{1mm} b |= | 10 | = 10$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \dfrac{(30\hspace{1mm} + \hspace{1mm}20)}{2} = \dfrac{50}{2} = 25$

$Percent\hspace{1mm} difference = [\dfrac{\left | 10 \right |}{25}]\times 100$

$Percent \hspace{1mm}difference = 0.4\times 100 = 40\%$

Let us now swap the values of both variables and see the result

Let $a = 20$ and $b =30$

$a\hspace{1mm}-\hspace{1mm}b = 20\hspace{1mm} – \hspace{1mm}30 = -10$

$| a\hspace{1mm} – \hspace{1mm}b |= | -10 | = 10$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \dfrac{(20\hspace{1mm}+\hspace{1mm}30)}{2} = \dfrac{50}{2} = 25$

$Percent\hspace{1mm} difference = [\dfrac{\left | 10 \right |}{25}]\times 100$

$Percent\hspace{1mm} difference = 0.4\times 100 = 40\%$

So, the percentage difference between any two numbers will remain the same even if initial and final values are swapped with each other.

Let us now calculate the percentage change for the same example.

Let initial value $x1 = 30$ and final value $x2 =20$

$x2-x1 = 20 – 30 = – 10$

$| x1 |= | 30 | = 30$

$Percent\hspace{1mm} change = [\dfrac{ – 10 }{30}]\times 100$

$Percent\hspace{1mm} change = -0.333\times 100 = -33.3\% $ or $33.3 \%$ decrease in the value.

Let us now swap the values of both variables, initial value = 20 and final value = 30 and see the result

Let initial value $x1 = 20$ and final value $x2 =30$

$x2\hspace{1mm}-\hspace{1mm}x1 = 30 \hspace{1mm}-\hspace{1mm} 20 =  10$

$| x1 |= | 20 | = 20$

$Percent\hspace{1mm} change = [\dfrac{  10 }{20}]\times 100$

$Percent\hspace{1mm} change = 0.5\times 100 = 50\%$ or $50\%$ increase in the value.

The above example should have cleared the confusion between percentage difference and percentage change and it also explains that percent difference does not tell us the direction of difference, i.e., which variable had a positive or negative percentage change as compared to the other. This directional difference is captured in percentage change.

Percent Difference between Two Numbers

So far, we have studied how to calculate the percent difference between two numbers. But a question arises when is it feasible to use the percent difference between two numbers?

Real-Life Examples of Percent Difference

• Let us look at some real-life examples and see where we can apply the method of a percent difference. Let us assume we have two sections of the 2^nd-grade class, section “A” and section “B”; section A has a strength of $35$ students while section B has a strength of $45$ students. In this case, we are comparing the strengths of two sections of the same class so we can easily apply the percent difference method as it will tell us about the percentage difference of class strengths between the two sections. The percent difference between the two sections is $25\%$.
• Let’s take another example and assume class A had $20$ students in January, and in three months, the class strength increased to $40$. In this case, we again have two numbers, $20$ and $40$, but it’s the same section, and the use of percentage change is suitable for this kind of example. The percent change shows that there has been a $100\%$ increase in the class strength. So, for a scenario that deals with an original value and an updated new value, We should use the percentage change to calculate the percentage increase or decrease. In contrast, percentage difference should be used when comparing the same thing, for example, comparing prices of two Toyota cars.
• Similarly, there is a difference between percent error and percent difference as well. Therefore, when comparing actual and estimated values, we will use percentage error to calculate this scenario’s percent error.

Limitation of Percent Difference

• The percent difference method has its limitation, and they are prominent when the difference between values of two numbers is very high. For example, suppose a multinational company consists of two major departments A) HR department B) Technical department. Now suppose in the year $2019$, the total number of employees working in the “HR department” were $500$ and in the “Technical department” were $900$. Thus, the percent difference between the two departments was approx—$ 57\%$.
• Assume that the company hires $100,000$ more technical staff in the year $2020$ while the number of staff in the” HR department” remains the same. Thus, the total number of employees in the “Technical department” would be $100,900$ and the percent difference for the year $2020$ would be $198\%$.
• Assume the company hires a further $100,000$ technical staff in 2021 while no recruitment is done for the “ HR department.” The total number of employees in the “Technical department” would be $200,900$ and the percent difference for the year $2021$ would be $199\%$. As we can see, there is not much of a difference between the percentage difference values of the year $2020$ and $2021$ even after hiring further $100,000$ persons. This indicates the limitation of a percent difference, i.e., whenever the difference of values between two numbers is huge, the percent difference may not be ideal for comparison. As the difference in the value of two numbers increases, the absolute difference also increases with it. Still, its effect is very little or negligible on percent difference because we are diving with the average of the two numbers.

Now that we have studied the percent difference and its limitations. The flow chart for the calculation of the percent difference is given below.

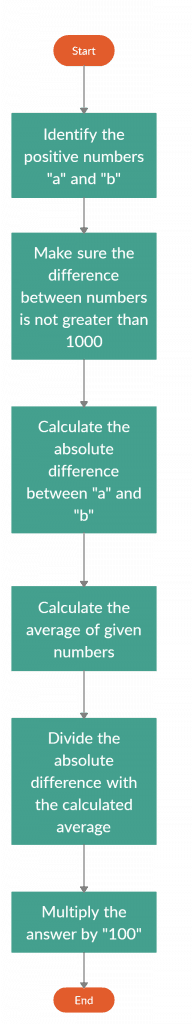
Example 2:  Car “A” is moving at $50$ Miles Per Hour, and car “B” is moving at $70$ Miles Per Hour. Calculate the percent difference of speed between these two cars.

Solution:

$a = 50$ and $b = 70$

$a\hspace{1mm}-\hspace{1mm}b = 50 \hspace{1mm}- \hspace{1mm}70 = -20$

$| a\hspace{1mm} – \hspace{1mm}b |= | -20 | = 20$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \frac{(50\hspace{1mm}+\hspace{1mm}70)}{2} = \frac{120}{2} = 60$

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)/2}]\times 100$

$Percent\hspace{1mm} difference = [\dfrac{\left | 20 \right |}{60}]\times 100$

$Percent \hspace{1mm}difference = 0.333\times 100 = 33.3\%$

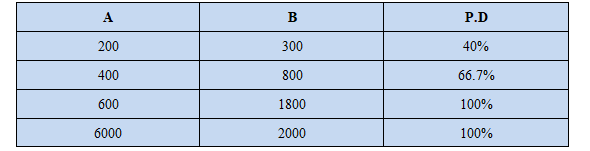
Example 3:  Calculate the percent difference between the numbers in the table given below.

Solution:

•  $ a = 200$ and $b = 300$

$a\hspace{1mm}-\hspace{1mm}b = 200\hspace{1mm} -\hspace{1mm} 300  = -100$

$| a\hspace{1mm} -\hspace{1mm} b |= | -100 | = 100$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \dfrac{(200\hspace{1mm}+\hspace{1mm}300)}{2} = \dfrac{500}{2} = 250$

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)/2}]\times 100$

$Percent\hspace{1mm} difference = [\dfrac{\left | 100 \right |}{250}]\times 100$

$Percent \hspace{1mm}difference = 0.4\times 100 = 40\%$

• Let $a = 800$ and $b = 400$

$a\hspace{1mm}-\hspace{1mm}b = 800\hspace{1mm} – \hspace{1mm}400 = 400$

$| a\hspace{1mm} -\hspace{1mm} b |= | 400 | = 400$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} =\dfrac{(800\hspace{1mm}+\hspace{1mm}400)}{3} = \frac{1200}{2} = 600$

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)/2}]\times 100$

$Percent\hspace{1mm} difference = [\dfrac{\left | 400 \right |}{600}]\times 100$

$Percent\hspace{1mm} difference = 0.666\times 100 = 66.7\%$

• Let $a = 600$ and $b = 1800$

$a\hspace{1mm}-\hspace{1mm}b = 600\hspace{1mm} – \hspace{1mm}1800 = – 1200$

$| a \hspace{1mm}-\hspace{1mm} b |= | -1200 | = 1200$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \dfrac{(600\hspace{1mm}+\hspace{1mm}800)}{2} = \frac{2400}{2} = 1200$

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{a+b/2}]\times 100$

$Percent\hspace{1mm} difference = [\dfrac{\left | 1200 \right |}{1200}]\times 100$

$Percent\hspace{1mm} difference = 1\times 100 = 100\%$

• Let $a = 6000$ and $b = 2000$

$a\hspace{1mm}-\hspace{1mm}b = 6000\hspace{1mm} – \hspace{1mm}2000 = 4000$

$| a\hspace{1mm} – \hspace{1mm}b |= | 4000 | = 4000$

$d\frac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \dfrac{(6000\hspace{1mm}+\hspace{1mm}2000}{2} = \dfrac{8000}{2} = 4000$

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)/2}]\times 100$

$Percent\hspace{1mm} difference = [\dfrac{\left | 4000 \right |}{4000}]\times 100$

$Percent\hspace{1mm} difference = 1\times 100 = 100\%$

Example 4: Adam has scored 300 goals in his entire football career while Steve has scored 100 goals. Calculate the percentage difference of goals between these two players

Solution:

Let $a = 300$ and $b = 100$

$a\hspace{1mm}-\hspace{1mm}b = 300\hspace{1mm} – \hspace{1mm}100 = -200$

$| a\hspace{1mm} – \hspace{1mm}b |= | -200 | = 200$

$\dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2} = \dfrac{(100\hspace{1mm}+\hspace{1mm}300)}{2}= \dfrac{400}{2} = 200$

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)/2}]\times 100$

$Percent\hspace{1mm} difference = [\dfrac{\left | 200 \right |}{200}]\times 100$

$Percent\hspace{1mm} difference = 1\times 100 = 100\%$

If we analyze example 3 and the last two rows of the table in example number 2, we can clearly see that if one number is 3 times greater than the other number, the percent difference is always 100%. Let us prove this in the following example.

Example 5: Prove that when $a = 3b$, the percent difference equals $100\%$.

Solution:

$Percent\hspace{1mm} difference = [\dfrac{\left | a\hspace{1mm}-\hspace{1mm}b \right |}{(a\hspace{1mm}+\hspace{1mm}b)/2}]\times 100$

When percent difference is $= 100\%$

$| a \hspace{1mm}-\hspace{1mm} b |= \dfrac{(a\hspace{1mm}+\hspace{1mm}b)}{2}$

$2\times (a\hspace{1mm}-\hspace{1mm}b) = a\hspace{1mm}+\hspace{1mm}b$

$2a\hspace{1mm} -\hspace{1mm}2b = a\hspace{1mm} + \hspace{1mm}b$

$a = b\hspace{1mm} +\hspace{1mm}2b$

$a =3b$