Percent Error – Explanation & Examples
Percent Error is used to calculate the relative or percent error between the experimental and the actual value. For example, we are trying to measure air pressure, and we know the actual value is 760mm Hg, but our experimental or measured value is 758 mm Hg. The relative difference between 760 mm Hg and 758mm Hg is calculated using the percent error formula.
The answer in percent error is represented in percentage, so we first need to understand a percentage concept. When we express a number as a fraction of 100 is said to be a percentage. For example, 10 percent (i.e., 10%) is equal to $\dfrac{10}{100}$; similarly, 2 percent is $\dfrac{2}{100}$. The percentage sign is denoted by “%,” and it is equal to 1/100.
Percent Error is the ratio of the absolute error and actual value multiplied by 100.
You should refresh the following concepts to understand the material discussed here.
- Percentage.
- Basic Arithmetic.
What is Percent Error
Percent error is calculated when there is a reference or actual value against which we compare our measured values. The difference between these two values is treated as the error.
These errors arise due to certain limitations in technology or human mistakes/misjudgments, and calculation of these errors during experiments is necessary. Percent error is used to calculate the error and present the error in percentage. As we stated above percent error is the ratio of the absolute error and actual value. Absolute error is the absolute value of the difference of the measured and the actual value, So percent error can be represented as.
Absolute error = |Actual value – Experimental value|
Percent error = [Absolute error/Actual Value] * 100.
We have discussed percent error so far, but there are other closely related terms and the difference between them is very subtle. You should know the difference between the following terms.
1. Absolute Error
2. Relative Error
3. Percent Error
Absolute Error: It is the difference between the actual value and the observed or measured value. The difference is given as an absolute value which means that we are interested in the magnitude of the error and ignore the sign.
$\color{blue}\mathbf{Absolute\hspace{2mm} Error = \left | Actual\hspace{2mm} value – Estimated\hspace{2mm} Value \right | }$
Relative Error: When we divide the absolute value by the actual value, it is called relative error. Here actual value is also taken as the absolute value. Hence the relative error cannot be negative.
$\color{blue}\mathbf{Relative\hspace{2mm} Error = \left | \dfrac{Absolute\hspace{2mm} Error}{Actual\hspace{2mm} value} \right | }$
Percent Error: When a relative error is multiplied by 100, it is known as percent error.
$\color{blue}\mathbf{Percent\hspace{2mm} Error = Relative\hspace{2mm} Error \times 100\%}$
How to Calculate Percent Error
Calculation of the percent difference is pretty simple and easy. But, first, you need to follow the steps given below.
- Identify the real or actual value of the quantity you are going to measure or observe.
- Take the experimental value of the quantity.
- Calculate the absolute error by subtracting the experimental value from the actual value
- Now divide the absolute error by the actual value, and the resulting value is also an absolute value, i.e., it cannot be negative.
- Express the final answer in percentage by multiplying the result in step 4 by $100$.
Percent Error Formula:
We can calculate percent error by using the formula given below.
$\mathbf{Percentage Difference = [\dfrac{\left | A.V\hspace{1mm} -\hspace{1mm} M.V \right |}{A.V}]\times 100}$
Here,
A.V = Actual value
M.V = Measured value or Estimated value.
Percent Error Mean Formula:
The percent error mean is the average of all the means calculated for a given problem or data. Its formula is given as.
$\mathbf{\sum_{i=1}^{n}[\dfrac{\left|A.V\hspace{1mm} -\hspace{1mm}M.V \right|}{\left|A.V \right|}]\times \frac{100}{n}\%} $
Difference between Percent Error, Standard Error, and Margin of Error:
Some terms are closely related, and students can confuse one term with the other. This section will explain the difference between percent, standard, and margin of error.
Percent Error: Percent error is used to measure error or discrepancy between the actual and the measured value.
Standard Error: This term is used in statistics to calculate the error between a sample and a population. When a sample is taken from a population, the standard error is used to measure the accuracy of that sample with a given population.
Margin of Error: The margin of error is also related to the population’s standard deviation and sample size. It is calculated by multiplying the standard error by the standard score.
Example 1: Allan bought a new football. The radius of the football is 8 inches. The actual radius of a football used internationally is 8.66 inches. You are required to calculate the percent error between these two values.
Solution:
$Actual \hspace{1mm}Value = 8.66 \hspace{1mm}and\hspace{1mm} Measured\hspace{1mm} or\hspace{1mm} observed\hspace{1mm} value = 8$
$Percentage\hspace{1mm} Error = \left |\dfrac{ Actual\hspace{1mm} Value \hspace{1mm}-\hspace{1mm} Observed\hspace{1mm} Value }{Actual\hspace{1mm} Value}\right|\times 100$
$A.V\hspace{1mm}- \hspace{1mm}O.V = 8.66\hspace{1mm} – \hspace{1mm}8 = 0.66$
$Percentage\hspace{1mm} error = \left|\dfrac{ 0.66 }{8.66}\right|\times 100$
$Percent\hspace{1mm} error = 0.0762\times 100 = 7.62\%$
Example 2: Calculate the percent error between the actual and experimental values in the table given below.
Actual Value | Experimental Value | Percent Error |
$10$ | $7$ | |
$11$ | $13$ | |
$15$ | $18$ | |
$6$ | $4$ |
Solution:
1).$Actual\hspace{1mm} Value = 10\hspace{1mm} and\hspace{1mm} Measured\hspace{1mm} or\hspace{1mm} observed\hspace{1mm} value = 7$
$Percentage\hspace{1mm} error = \left|\dfrac{ Actual\hspace{1mm} Value\hspace{1mm}-\hspace{1mm} Observed\hspace{1mm} Value }{Actual \hspace{1mm}Value}\right|\times 100$
$A.V\hspace{1mm}-\hspace{1mm} M.V = 10 \hspace{1mm}-\hspace{1mm}7 = 3$
$Percentage\hspace{1mm} error = \left |\dfrac{ 3 }{10}\right|\times 100$
$Percent\hspace{1mm} error = 0.3\times 100 = 30\%$
2). $Actual\hspace{1mm} Value = 11\hspace{1mm} and\hspace{1mm} Measured\hspace{1mm} or\hspace{1mm} observed\hspace{1mm} value = 13$
$Percentage\hspace{1mm} error = \left|\dfrac{ Actual\hspace{1mm} Value\hspace{1mm}-\hspace{1mm} Observed \hspace{1mm}Value }{Actual \hspace{1mm}Value}\right|\times 100$
$A.V\hspace{1mm}-\hspace{1mm} M.V = 11 \hspace{1mm}-\hspace{1mm} 13 = -2$
$Percentage\hspace{1mm} error = \left |\dfrac{ -2 }{11}\right|\times 100$
$Percent\hspace{1mm} error = 0.1818\times 100 = 18.18\%$
3). $Actual\hspace{1mm} Value = 15\hspace{1mm} and\hspace{1mm} Measured\hspace{1mm} or\hspace{1mm} observed\hspace{1mm} value = 18$
$Percentage\hspace{1mm} error = \left|\dfrac{ Actual\hspace{1mm} Value\hspace{1mm}-\hspace{1mm} Observed \hspace{1mm}Value }{Actual \hspace{1mm}Value}\right|\times 100$
$A.V\hspace{1mm}-\hspace{1mm} M.V = 15 \hspace{1mm}-\hspace{1mm} 18 = -3$
$Percentage\hspace{1mm} error = \left|\dfrac{ -3 }{15}\right|\times 100$
$Percent\hspace{1mm} error = 0.2\times 100 = 20\%$
4).$Actual \hspace{1mm}Value = 6\hspace{1mm} and\hspace{1mm} Measured\hspace{1mm} or\hspace{1mm} observed\hspace{1mm} value = 4$
$Percent\hspace{1mm} Error = \left|\dfrac{ Actual\hspace{1mm} Value\hspace{1mm}-\hspace{1mm} Observed \hspace{1mm}Value }{Actual \hspace{1mm}Value}\right|\times 100$
$A.V\hspace{1mm}-\hspace{1mm} M.V = 16 \hspace{1mm}-\hspace{1mm} 20 = -4$
$Percentage\hspace{1mm} Error = \left|\dfrac{ -4 }{16}\right|\times 100$
$Percent\hspace{1mm} difference = 0.25\times 100 = 25\%$
Actual Value | Experimental Value | Percent Error |
$10$ | $7$ | $30\%$ |
$11$ | $13$ | $18.18\%$ |
$15$ | $18$ | $20\%$ |
$16$ | $20$ | $25\%$ |
Example 3: William wants to buy a new car for his son. Due to the pandemic, the estimated increased price at which the car is available is 130,000 dollars while the actual value of the car is 100,000 dollars. You are required to help William in the calculation of the percent error between these two prices.
Solution:
$Actual \hspace{1mm}Value = 15\hspace{1mm} and\hspace{1mm} Measured \hspace{1mm} or\hspace{1mm} observed \hspace{1mm} value = 18$
$Percentage\hspace{1mm} error = \left|\dfrac{ Actual\hspace{1mm} Value\hspace{1mm}-\hspace{1mm} Observed\hspace{1mm} Value }{Actual\hspace{1mm} Value}\right|\times 100$
$A.V\hspace{1mm}-\hspace{1mm} M.V = 15\hspace{1mm} -\hspace{1mm} 18 = -3$
$Percentage\hspace{1mm} error = \left|\dfrac{ -3 }{15}\right|\times 100$
$Percent\hspace{1mm} error = 0.2\times 100 = 20\%$
Example 4: Mayer held a birthday party. Mayer estimated that 200 people will attend his birthday party but the actual amount of people who attended the function were 180. You are required to calculate the absolute error, relative error, and percent error.
Solution:
$Actual\hspace{1mm} Value = 180 \hspace{1mm}and\hspace{1mm} Estimated\hspace{1mm} value = 200$
$Absolute\hspace{1mm} error = |Actual \hspace{1mm}value\hspace{1mm} – \hspace{1mm}Measured\hspace{1mm} value| = |180\hspace{1mm} -\hspace{1mm} 200| = |-20| = 20$
$Relative\hspace{1mm} error = \left|\dfrac{Absolute\hspace{1mm} error }{Actual\hspace{1mm} Value}\right|$
$Relative\hspace{1mm} error = \left|\frac{20 }{180}\right|= 0.1111$
$Percent\hspace{1mm} error = Realtive error\times 100 = 20\%$
$Percent\hspace{1mm} error = 0.1111\times 100 = 11.11\%$
Example 5: Mason started a restaurant in August 2021 and invested a lot of money as he expected to generate good revenue through this restaurant. The expected and actual income of the first four months is given below. You are required to calculate the percent error mean.
Month | Expected Income (Dollars) | Actual Income (Dollars) | Percent Error |
August | $2500$ | $1700$ | |
September | $3500$ | $2500$ | |
October | $4000$ | $2800$ | |
November | $5000$ | $3900$ |
|
Solution:
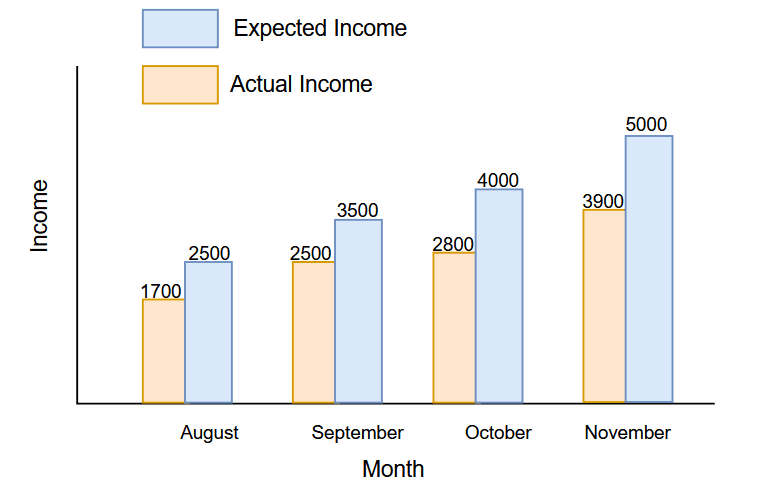
We can give a percent error calculation for the first four months as.
Month | Absolute Difference | Relative Error | Percent Error |
August | $800$ | $0.47$ | $47\%$ |
September | $1000$ | $0.4$ | $40\%$ |
October | $1200$ | $0.42$ | $42\%$ |
November | $1100$ | $0.282$ | $28.2\%$ |
P.E.M = $\dfrac{$47\%\hspace{1mm}+\hspace{1mm}40\%\hspace{1mm}+\hspace{1mm}42\%\hspace{1mm}+\hspace{1mm}28.2\%$}{$4$} = 39.3\ %$
we can also calculate percent error mean by using relative error values.
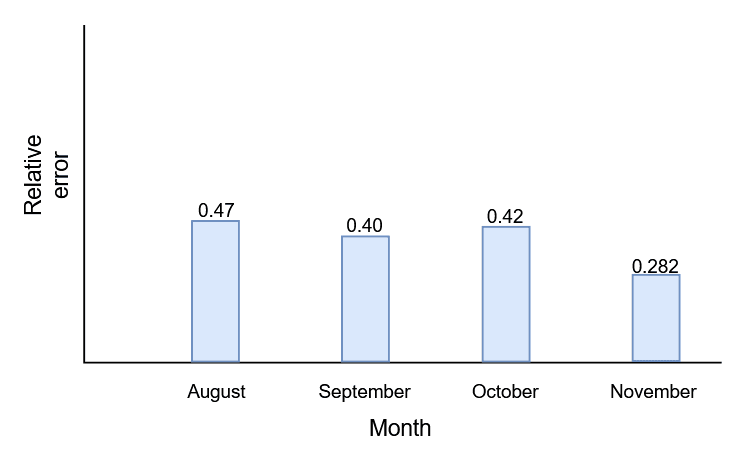
P.E.M = $[\dfrac{$0.47\hspace{1mm}+\hspace{1mm}0.40\hspace{1mm}+\hspace{1mm}0.42\hspace{1mm}+\hspace{1mm}0.282$}{$4$}] \times 100 = 39.3\ %$
