Polar Coordinates – Definition, Conversion, and Examples

Polar coordinates help us represent objects or relationships that are centrosymmetric (symmetric with respect to a common center).  The polar coordinate system, along with the rectangular coordinate system, is one of the most used and most helpful coordinate systems there are. In fact, there are instances when a polar coordinate system will be more helpful to us than the rectangular coordinate system.

Polar coordinates give us an alternative way to represent points on a plane. The polar coordinate system measures the polar angle and radial distance of the coordinate from the center called the pole.

Seeing how important polar coordinates are and their coordinate system, it is essential that we understand its basic components and have a strong foundation on the fundamentals. By the end of our discussion, we want you to master the following:

• Identifying the core components of polar coordinates.
• Knowing how to identify and plot polar coordinates on a plane.
• Understanding how polar coordinates are represented on the plane.

This article will thoroughly discuss these points, so take some notes and by the end of this article, you should be able to follow through with our explanations on the sample problems we’ve prepared!

What are polar coordinates?

Polar coordinates are represented by the ordered pair, $(r, \theta)$, where $\boldsymbol{r}$ is the distance of the polar coordinate from the pole (or origin) and $\boldsymbol{\theta}$ is the angle measured in standard position.

In the past, we’ve learned about rectangular coordinates, $(x, y)$, and its coordinate system. The ordered pair, $(x, y)$, tells us that we’ve moved the point $x$ units horizontally and $y$ units vertically from the origin.

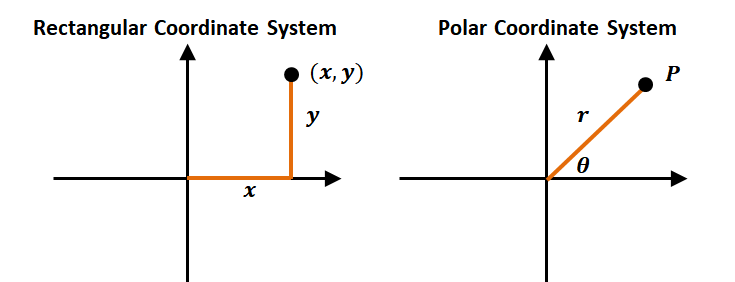
In the polar coordinate system, we start with a starting point, $O$, which we call the pole (similar to the rectangular coordinate system’s origin). From the point, $O$, we establish a polar axis – a horizontal ray set from the pole to the right. The polar axis, in a way, corresponds to the positive $x$-axis of the rectangular coordinate system.

The polar coordinate, $P(r, \theta)$, is set in the polar plane so that the distance between $O$ and $P$ is equal to $r$. The value of $\theta$ is measured based on the angle formed by the line segment, $OP$, and the polar axis.

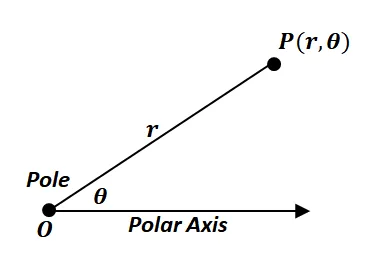
We call $r$ the radial distance (sometimes called the modulus) and $\theta$ the polar angle. When dealing with polar coordinates and coordinate system, it helps if you remember the following conventions by heart:

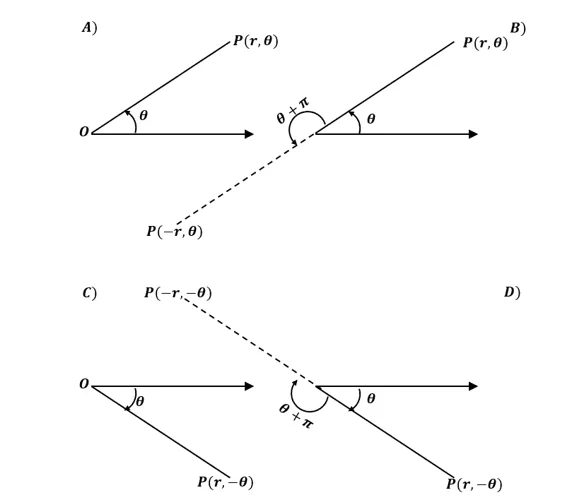
The four images shown above cover all four possible positions of a polar coordinate. From this, we can see that it makes sense that we normally use $\theta$ within $(-\pi, \pi)$. Of course, we can still work with angles. In fact, polar angles can have multiple representations.

 In the next sections, we’ll explore the relationships between the rectangular and polar coordinates. We’ll also understand how we can graph these polar coordinates on both the rectangular coordinate and the polar plane.

How to find polar coordinates?

If we have a Cartesian plane, we also have a polar plane – with its own orientation. Since the polar coordinate is dependent on the radial distance and the polar angle, we expect the polar plane to be circumferential. The “polar grids” are centered at the pole with the grids formed by circles with incremental radii and rays are formed at incremental angles.

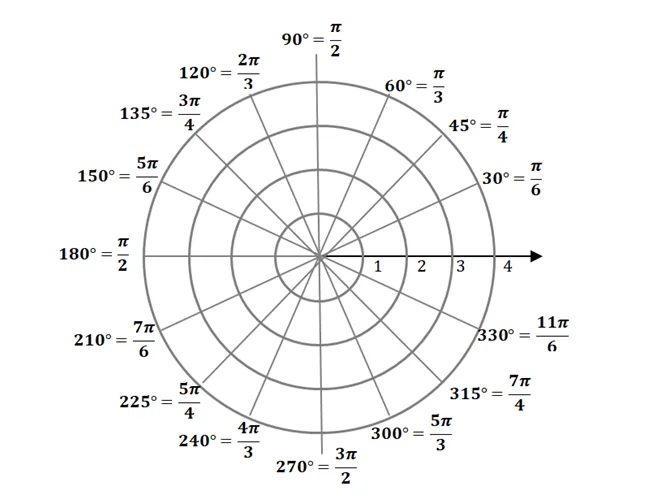
Here’s how a polar plane looks like and we’ve included the angles (both in degrees and in radians) as a guide. When asked to locate the position of a polar coordinate, check the values of $r$ and $\theta$:

• Use the absolute value of $r$ and count $r$ steps from the pole.
• Check if the angle is positive or negative then starting from the polar axis, rotate at an angle of $\theta$ in the counterclockwise or clockwise direction, respectively.

For example, if we want to find the location of $\left(3, \dfrac{\pi}{4} \right)$ by finding the position that is $3$ units away from the pole. Now, since $\dfrac{\pi}{4}$ is positive, the polar coordinate is located along the segment that forms an angle of $\dfrac{\pi}{4}$ with the polar axis.

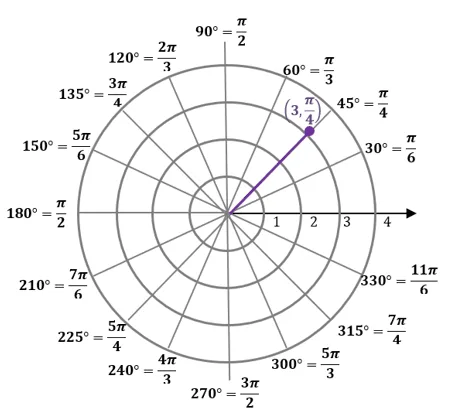
We’ll use a similar approach when finding the value of the polar coordinate.

• We find the radial distance of the polar coordinate from the pole. This value represents $r$.
• Find the angle formed by the segment connecting the polar coordinate and the pole. The polar angle formed will represent $\theta$.

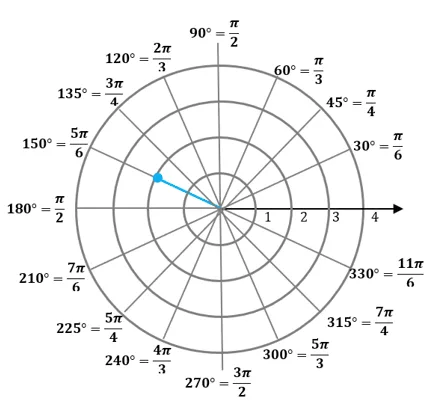
Let’s use this to find the polar coordinate’s value shown above. Since the polar coordinate is located $2$ units away from the pole, $r = 2$. The angle formed by segment and the polar axis is $150^{\circ}$ or $\dfrac{5\pi}{6}$. This means that the polar coordinate is equal to $\left(r, \theta\right) = (12, 150^{\circ}) = \left(12, \dfrac{5\pi}{6}\right)$.

We’ll be dealing more with polar planes when we learn about polar equations and curves. For now, let’s focus on learning how to plot different polar points.

How to graph polar coordinates?

We can graph polar coordinates with or without the polar planes. As long as we know the value and signs of $r$ and $\theta$, we’ll be able to plot any polar coordinates. Use the guideline below to help you graph any polar coordinate:

• Set up the polar plane – from the pole and polar axis, construct concentric circles with incremental radii.
• Use the following angles as markers: $0^{\circ}$ and $180^{\circ} = \pi$ representing the positive and negative horizontal axis, respectively. Similarly, $90^{\circ} = \dfrac{\pi}{2}$ and $270^{\circ} = \dfrac{3\pi}{2}$ are situated at what we know as the positive and negative vertical axis.
• Identify the radial distance ($r$) and the polar angle ($\theta$) of the polar coordinate.
• Locate where the polar coordinate lies based on $\theta$.

• Determine whether $r$ is positive or negative and apply the following:

To better understand the process of plotting polar coordinates, let’s try to graph their polar coordinates: $(2, 135^{\circ})$ and  $(-2, 135^{\circ})$. We can plot these two polar coordinates in one polar plane, so we can construct one polar plane with at least two concentric circles.

The polar angle, $\theta = 135^{\circ}$, is located in the second quadrant, so mark the terminal side as a guide then find the intersection between the terminal side and the circle with a radius of $2$.

The intersection represents the polar coordinate, $(2, 135^{\circ})$. For the second polar coordinate, since $r = -2$, simply reflect the existing polar coordinate over so that it lies opposite to the terminal side of the previous line segment.

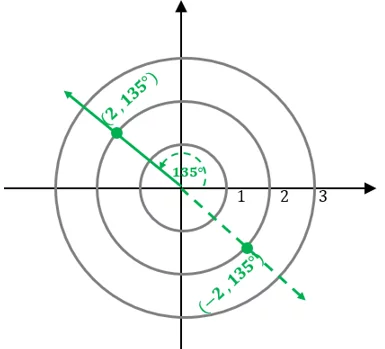
Check out the polar plane shown above to see how the two polar coordinates are plotted on one plane. We’ve now covered the fundamentals of polar coordinates, so it’s time that we understand how we can relate rectangular coordinates and polar coordinates to each other.

How to convert polar coordinates?

In the earlier section, we’ve shown you two coordinate systems: rectangular and polar coordinate systems. Why don’t we merge the two systems to see how one relates to the other?

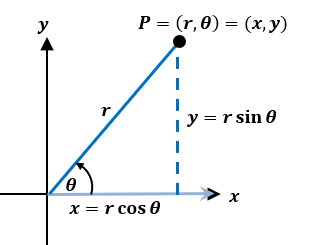
The graph above shows us how polar and rectangular coordinates relate to each other. The polar axis lies along the positive axis and the pole lies in the same position as the origin. From the figure, we can use previous trigonometric properties to establish the relationship between these two coordinate systems.

\begin{aligned}x^2 + y^2 &= r^2\\\sin \theta = \dfrac{y}{r},\phantom{x} \cos \theta &= \dfrac{x}{r},\phantom{x} \tan \theta = \dfrac{y}{x} \end{aligned}

These four relationships apply when the polar coordinate, $P(r, \theta)$, lies in any of the four quadrants and when $r > 0$ or $r < 0$. Let’s rewrite the expressions shown above to summarize the relationship between the two coordinates.

Use these relationships to convert polar coordinates to rectangular coordinates. We can also convert rectangular coordinates to polar coordinates. Let’s begin with the latter since it’s more straightforward.

Converting Polar Coordinates to Rectangular Coordinates

 We can convert the polar coordinate, $(r, \theta)$, to rectangular coordinates, $(x, y)$, by:

• Using $r$ and $\theta$ to evaluate $x = r \cos\theta$ and $y= \sin \theta$.
• Write the rectangular coordinate as $(x, y)$.

Here are two examples of converting polar coordinates to rectangular coordinates:

In case you need a refresher on evaluating trigonometric functions, head over to this link. Now, let’s see how we can reverse the process and convert rectangular coordinates to polar coordinates.

Converting Polar Coordinates to Rectangular Coordinates

This process is more complicated and since we can represent polar coordinates in infinitely many ways, we’ll stick with these conventions to simplify the process: 1) $r$ is positive ($r > 0$) and 2) $\theta$ is the smallest possible polar angle for the polar coordinate ($0 \leq \theta < 2\pi$).

• Sketch the point to help you determine which quadrant $(x, y)$ lies.
• Calculate the distance of the point, $(x, y)$ from the origin to find $r$: $r = \sqrt{x^2 + y^2}$.
• Find the value of the polar angle, $\theta$, using $\tan \theta = \dfrac{y}{x}$: $\theta = \tan^{-1} \left(\dfrac{y}{x}\right)$, where $\theta$ is within the quadrant.

This means that we can now convert the rectangular coordinate, $(2, -2)$, to its polar form. First, let’s plot $(2, -2)$ to determine where it lies.

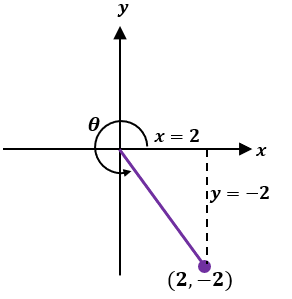
From this, we can see that the rectangular coordinate, $(2, -2)$, lies in the fourth quadrant. Now, calculate the distance of $(2, -2)$ from the origin.

\begin{aligned}r &= \sqrt{ x^2 + y^2 }\\&= \sqrt{(2)^2 + (-2)^2}\\&= \sqrt{8}\\&= 2\sqrt{2}\end{aligned}

Use $\tan \theta = \dfrac{y}{x}$ and take the tangent inverse to find the value of $\theta$. Keep in mind that $\theta$ lies in the fourth quadrant.

\begin{aligned}\tan \theta &= \dfrac{-2}{2}\\ \theta &= \tan^{-1} (-1)\\&= \dfrac{7\pi}{4}\\&= 315^{\circ}\end{aligned}

Now that we have $r = 2\sqrt{2}$ and $\theta = \dfrac{7\pi}{4}$, the rectangular coordinate, $(2, -2)$, is equal to $\left(2\sqrt{2}, \dfrac{7\pi}{4}\right)$ in polar form. We  can also write $(2, -2)$ as $(2\sqrt{2}, 315^{\circ})$.

When the rectangular coordinate $(x, y)$ lies on a horizontal or vertical axis, a much easier approach is by plotting the point then:

• Using a positive value for $r$.
• Determine the angle, $\theta$, representing the particular axis that the point is lying in.

Let’s try this simpler approach to convert,$(-4, 0)$, to a polar coordinate. Begin by plotting the point on the $xy$-axis.

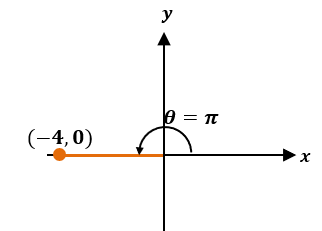
The distance of the point, $(-4, 0)$, is $r  = 4$ by inspection but we can also confirm this using the formula, $r= \sqrt{x^2  + y^2}$.

\begin{aligned}r &= \sqrt{ x^2 + y^2 }\\&= \sqrt{(-4)^2 + (0)^2}\\&= \sqrt{16}\\&= 4\end{aligned}

The angle lies on the negative $x$-axis, so $\theta = \pi$. This means that the rectangular coordinate, $(-4, 0)$, is equivalent to $(2, \pi)$.

We’ve now covered all the core concepts for polar coordinates. For now, take a quick review of all the concepts we’ve discussed, and when you’re ready, head over to the next section to work on more problems!

Example 1

Plot the following polar coordinates in one polar plane. Label each polar coordinate.

a. $(2, 240^{\circ})$
b. $\left(-3, \dfrac{\pi}{2} \right)$
c. $\left(1, \dfrac{5\pi}{3} \right)$

Solution

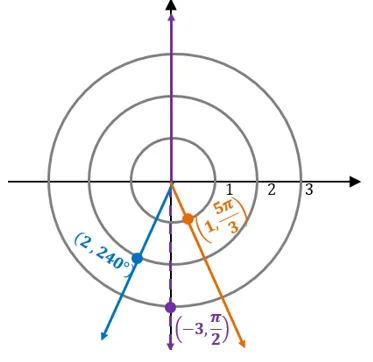
Since the highest absolute of $r$ among these three coordinates is $3$, we can construct a polar plane with three circles centered at the origin and with three incremental radii.

Let’s break down each of the steps needed to graph each of the polar coordinates.

Here’s the polar plane containing all three polar coordinates:

Example 2

The polar coordinate, $\left(4, \dfrac{\pi}{4}, \right)$, can be represented in multiple ways. Find another form of this polar coordinate where $r$ is negative and $0 < \theta < 2\pi$.

Solution

As we have mentioned in our discussion, one polar coordinate can be represented in an infinite number of ways. We can rewrite a polar coordinate with a positive radial distance, $r$, to a polar coordinate with a negative $r$ using the relationship shown below.

\begin{aligned}(r, \theta) &= (-r, \theta + \pi )\end{aligned}

Use $r = 4$ and $\theta = \dfrac{\pi}{4}$ into this equation to find another polar coordinate equivalent to  $ \left(4, \dfrac{\pi}{4}, \right)$.

\begin{aligned}\left(4, \dfrac{\pi}{4}, \right)&= \left(-1\cdot 4, \dfrac{\pi}{4} + \pi \right)\\ &= \left(-4, \dfrac{5\pi}{4} \right )\end{aligned}

Hence, another polar coordinate equivalent to $\left(4, \dfrac{\pi}{4}, \right)$ is $\left(-4, \dfrac{5\pi}{4} \right )$, where $r$ is negative and $0 < \theta < 2\pi$.

Example 3

Convert the following polar coordinates to their respective rectangular forms.

a. $\left(4, \dfrac{3\pi}{2}\right)$
b. $(-6, 120^{\circ})$
c. $\left(12, \dfrac{11\pi}{6}\right)$

Solution

For each of the polar coordinate, we simply use the corresponding radial distance, $r$, and the polar angle, $\theta$, into the following formulas.

\begin{aligned} x &= r \cos \theta \\ y &= r\sin \theta \\\\(r, \theta) &= (x, y)\end{aligned}

The table below summarizes our calculations for all three items:

Example 4

What is the polar coordinate that has a rectangular coordinate form of $(-2\sqrt{3}, 2)$?

Solution

Let’s plot the rectangular coordinate,$(-2\sqrt{3}, 2)$, to see which quadrant it lies in.

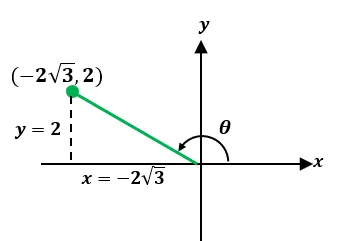
From this, we can see that $\theta$ lies in the second quadrant. Find the value of $r$ by using the formula, $r = \sqrt{x^2 + y^2}$.

\begin{aligned}r &= \sqrt{(-2\sqrt{3})^2 + (2)^2}\\&= \sqrt{12 + 4}\\&= 4\end{aligned}

Use $\tan \theta = \dfrac{y}{x}$ to find the value of $\theta$. Make sure that the angle lies in the second quadrant.

\begin{aligned} \tan \theta &= \dfrac{2}{-2\sqrt{3}}\\ \theta &= \tan^{-1} \left(-\dfrac{1}{\sqrt{3}}\right)\\ &= -30^{\circ}\\&= 150^{\circ}\end{aligned}

This means that $\theta = 150^{\circ} = \dfrac{5\pi}{6}$. Now, let’s write the polar coordinate, $(r, \theta) = (4, 150^{\circ})$. We can also write it so that $\theta$ is in its radian form :$\left(4, \dfrac{5\pi}{6}\right)$.

Practice Questions

1. Plot the following polar coordinates in one polar plane. Label each polar coordinate.
a. $(-3, 150^{\circ})$
b. $\left(2, \dfrac{3\pi}{2} \right)$
c. $\left(1, \dfrac{7\pi}{4} \right)$
2. The polar coordinate, $\left(2, \dfrac{\pi}{6}, \right)$, can be represented in multiple ways. Find another form of this polar coordinate where $r$ is negative and $0 < \theta < 2\pi$.

3. The polar coordinate, $\left(3, \dfrac{5\pi}{4}, \right)$, can be represented in multiple ways. Find another form of this polar coordinate where $r$ is positive and $-2\pi < \theta < 0$.

4. Convert the following polar coordinates to their respective rectangular forms.
a. $\left(-6, \dfrac{\pi}{2}\right)$
b. $(8, 240^{\circ})$
c. $\left(14, \dfrac{5\pi}{6}\right)$
5. What is the polar coordinate that has a rectangular coordinate form of $(-6, 6\sqrt{3})$?
6. What is the polar coordinate that has a rectangular coordinate form of $(0, 8)$?

Answer Key

1.

2. $\left(2, \dfrac{\pi}{6}, \right) = \left(-2, \dfrac{5\pi}{6}, \right)$
3. $\left(3, \dfrac{5\pi}{4}, \right) = \left(3, -\dfrac{3\pi}{4}, \right) $
4.
a. $\left(-6, \dfrac{\pi}{2}\right) = (0, -6)$
b. $(8, 240^{\circ}) = (-4, -4\sqrt{3})$
c. $\left(14, \dfrac{5\pi}{6}\right) = (-7\sqrt{3},7) $
5. $(-6, 6\sqrt{3}) = \left(12, \dfrac{2\pi}{3}\right)$
6. $(0, 8) = \left(8, \dfrac{\pi}{2}\right)$