- Home
- >
- Polar form – General Form, Conversion Rules, and Examples
JUMP TO TOPIC
Polar form – General Form, Conversion Rules, and Examples
 Polar forms are one of the many ways we can visualize a complex number. They are a way for us to visualize complex numbers on a complex plane as vectors.
Polar forms are one of the many ways we can visualize a complex number. They are a way for us to visualize complex numbers on a complex plane as vectors.
A complex number in the polar form will contain a magnitude and an angle to guide us with the complex number’s orientation.
The polar forms of complex numbers help us visualize and treat the complex numbers as quantities that have distance and direction – through the polar coordinate system.
When discussing polar forms, we’re expecting to make use of past and new concepts. In this article, we’ll tackle the following topics:
- A refresher on polar coordinates and how we can convert a rectangular coordinate to a polar coordinate.
- A guide on how we can represent complex numbers in polar form and coordinate system.
- Learning how to plot complex numbers in the context of their polar form’s elements.
First, let’s recall what we know about polar and rectangular forms. Make sure to keep a handy notepad or note-taking app since this will be a thorough discussion of polar forms and complex numbers in polar form.
What is a polar form?
The polar form of numbers, in general, makes use of the number’s modulus (or distance from the origin) and the angle it forms concerning the $x$-axis.
Some examples of coordinates in polar form are: $(2, 45^{\circ})$, $\left(3, \dfrac{\pi}{4}\right)$, and $(5, 1.2)$.
- The first coordinates, $\{2, 3, 5\}$, represent the distance of the coordinate from the origin.
- The second coordinates, $ \left\{ 45^{\circ}, \dfrac{\pi}{4}, 1.2 \text{ radians}\right \}$, represent the angle formed along the $x$-axis.
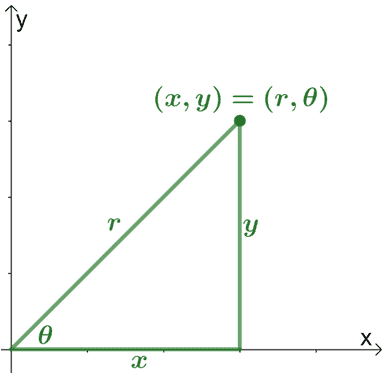
Here’s a helpful diagram to better understand how a rectangular coordinate may differ when represented by its polar form. Let’s go ahead and inspect its elements.
- $r$ represents the distance of the point from the origin
- $\theta$ represents the angle formed by $r$ with the $x$-axis
- $(x, y)$ is the rectangular form of a point while $(r, \theta)$ represents its polar form
We can even relate $x$, $y$, $r$, and $\theta$, so we can better understand how rectangular and polar forms differ from each other.
| \begin{aligned}x&= r\cos \theta \\ y &= r \sin \theta\\x^2 + y^2 &= r^2 \\ \tan \theta &= \dfrac{y}{x}\end{aligned} |
Here’s an example on how we can convert a rectangular coordinate, $(1, \sqrt{3})$, to its polar form. We have $x = 1$ and $y = \sqrt{3}$. Using these values, we can now find the value of $r$ and $\theta$ as shown below.
| $\boldsymbol{x^2 + y^2 = r^2}$ | $\boldsymbol{\tan \theta = \dfrac{y}{x}}$ |
| $\begin{aligned}r &= \sqrt{x^2 + y^2}\\ &= \sqrt{(1)^2 + (\sqrt{3})^2}\\&= \sqrt{4}\\&= 2\end{aligned}$ | $\begin{aligned}\tan \theta &= \dfrac{\sqrt{3}}{1}\\\tan \theta &= \sqrt{3}\\\theta &= \tan^{-1} \sqrt{3}\\&=60^{\circ}, 240^{\circ}\end{aligned}$ Since the point lies on the first quadrant, $\theta = 60^{\circ}$. |
This means that the rectangular coordinate, $(1, \sqrt{3})$, is equal to $(2, 60^{\circ})$ in polar form.
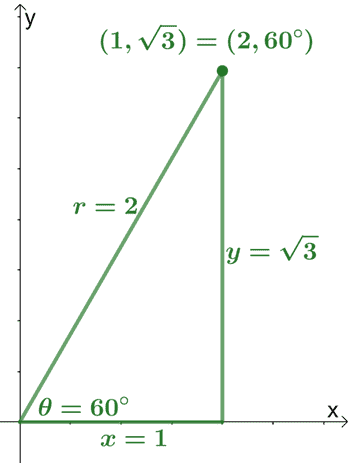
The graph above will help us understand how the rectangular and polar coordinates can coincide in one graph. These introductory concepts will also help us define complex numbers in terms of $r$ and $\theta$ as well.
How to write a complex number in polar form?
When learning about complex numbers, we have learned how $a + bi$ can be graphed on a complex plane where $a$ replaces the $x$-coordinate $b$ replaces the $y$-coordinate.
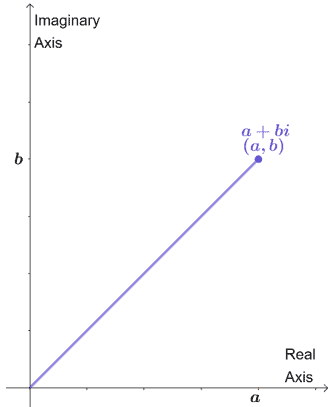
Since the complex plane has similar dynamics with the rectangular coordinate. With the real axis representing the $x$-axis and the imaginary axis representing the $y$-axis.
Let’s rewrite the polar form we have from the earlier section and see how this applies for complex numbers.
| $ \begin{aligned}x&= r\cos \theta \\ y &= r \sin \theta\\x^2 + y^2 &= r^2 \\ \tan \theta &= \dfrac{y}{x}\end{aligned}$ | $ \begin{aligned}a&= r\cos \theta \\ a &= r \sin \theta\\a^2 + b^2 &= r^2 \\ \tan \theta &= \dfrac{b}{a}\end{aligned}$ |
This also means that we can write $a + bi$ as $r \cos \theta + r\sin \theta i= r(\cos \theta + \sin \theta i)$. The expression $r(\cos \theta + \sin \theta i)$ is the polar form of the complex number.
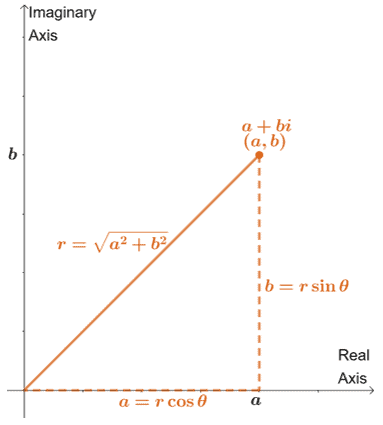
We can also see that $r$ is equal to the complex number’s modulus or absolute value from the table.
This means that we can write complex numbers in terms of $r$ and $\theta$. In fact, a well-known abbreviation of a complex number’s polar is $r\text{cis} \theta$.
How to convert to polar form?
We can convert numbers in polar to rectangular form. Similarly, we can convert numbers in rectangular to polar form.
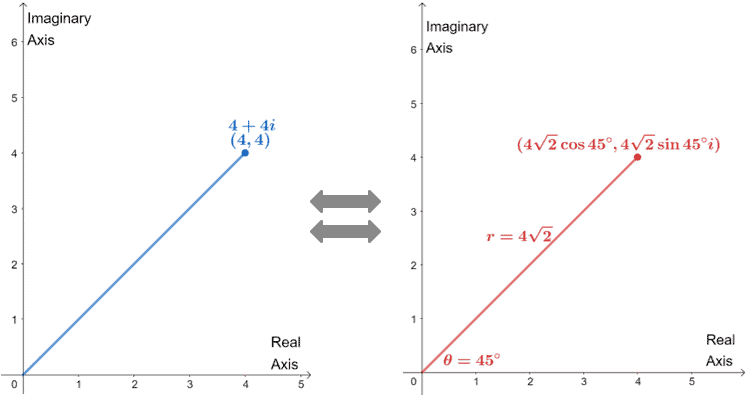
The graphs above show how the two forms (rectangular and polar) reflect the same complex number and a point in the same position.
It helps to always go back to this group of equations whenever in doubt with a step or two.
| \begin{aligned}x&= r\cos \theta \\ y &= r \sin \theta\\x^2 + y^2 &= r^2 \\ \tan \theta &= \dfrac{y}{x}\end{aligned} |
We’ve summarized helpful steps to remember in converting complex numbers in the rectangular form to polar form. Don’t worry. We’ve also prepared steps for doing the reverse.
How to convert rectangular form to polar form?
We can find the complex number’s polar form by following the steps below.
- Find the complex number’s absolute value, $|z| = r = \sqrt{a^2 + b^2}$.
- Find the value of $\theta$ using $\tan \theta = \dfrac{b}{a}$.
- Substitute the values of $r$ and $\theta$ into the expression, $r(\cos \theta + \sin \theta i)$.
Whenever stuck with writing complex numbers in polar form, always go back to these three steps.
Why don’t we apply this to write $1 + \sqrt{3}i$ in polar form?
Let’s find the value of $r$ by finding the absolute value of $2 + i$.
$\begin{aligned}r &= \sqrt{(1)^2 + (\sqrt{3})^2}\\&= \sqrt{1 + 3}\\&= 2\end{aligned}$
Now, we use $a = 1$ and $b = \sqrt{3}$ to find the value of $\theta$. Since both $a$ and $b$ are positive, $\theta$ lies on the first quadrant.
$\begin{aligned}\tan \theta &= \dfrac{1}{\sqrt{3}}\\\theta &= \tan^{-1} \dfrac{1}{\sqrt{3}}\\&=30\circ\end{aligned}$
Hence, $r = 2$ and $\theta = 30^{\circ}$.
Using these values, we can now write $1 + \sqrt{3}i$ as in polar form, $r(\cos \theta + \sin \theta i)$.
$\begin{aligned}r(\cos \theta + \sin \theta i)&= 2(\cos 30^{\circ} + \sin 30^{\circ}i)\\&=2\left(\dfrac{\sqrt{3}}{2}+ \dfrac{1}{2}i \right )\\&=2 \cdot \dfrac{\sqrt{3}}{2} + 2 \cdot \dfrac{1}{2}i\\&= \sqrt{3} + i\end{aligned}$
A common abbreviation used for complex numbers’ polar forms is $r \text{cis} \theta$, so $1 + \sqrt{3}i$ will also be equal to $2 \text{cis} 30^{\circ}$.
How to convert polar form to rectangular form?
Converting polar forms to rectangular forms is more straightforward. We can evaluate the values of $r\cos \theta$ and $r \sin \theta$ to find the rectangular form of the coordinate.
Given $(r\cos \theta, r\sin \theta)$, perform the following steps to convert polar coordinate to rectangular form:
- Find the values of $r\cos \theta$ and $r\sin \theta$.
- Write the results in order as $(x, y)$.
If given a complex number in polar form, we can simply write $(x, y)$ as $(a, b)$ instead and return $a + bi$.
For example, if we want to convert the complex number, $4\left(\cos \dfrac{\pi}{4} + \sin \dfrac{\pi}{4}\right)$, we simply evaluate $\cos \dfrac{\pi}{4}$ and $\sin \dfrac{\pi}{4}$.
$\begin{aligned}\cos \dfrac{\pi}{4} &= \dfrac{\sqrt{2}}{2}\\\sin \dfrac{\pi}{4} &= \dfrac{\sqrt{2}}{2}\\4\left(\cos \dfrac{\pi}{4} + \sin \dfrac{\pi}{4}i\right)&= 4 \left(\dfrac{\sqrt{2}}{2} +\dfrac{\sqrt{2}}{2}i\right)\\&=4 \cdot \dfrac{\sqrt{2}}{2} + 4 \cdot \dfrac{\sqrt{2}}{2}i\\&=2\sqrt{2} + 2\sqrt{2}i\end{aligned}$
This means that $2 \text{cis} \dfrac{\pi}{4}$ is equal to $2\sqrt{2} + 2\sqrt{2}i$.
We can apply a similar process when converting any polar form to a rectangular form.
How to multiply and divide complex numbers in polar form?
We’ve learned how to multiply and divide complex numbers in the past, but what if we’re given two complex numbers in polar forms?
Let’s say we have $z_1 = r_1 (\cos \theta_1 + i \sin \theta_1)$ and $z_2 = r_2 (\cos \theta_2 + i \sin \theta_2)$.
To find their product, we can multiply the two moduli, $r_1$ and $r_2$, and find the cosine and sine of the sum of $\theta_1$ and $\theta_2$.
$z_1 z_2 = r_1 r_2 [\cos( \theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)]$
We apply a similar process to find the quotient of two complex numbers in polar form. Divide $r_1$ by $r_2$ and find the cosine and sine of the difference between $r_1$ and $r_2$.
$\dfrac{z_1}{z_2}= \dfrac{r_1}{r_2} [\cos(\theta_1 – \theta_2) + i\sin (\theta_1 – \theta_2)]$
This means that we can immediately multiply and divide them when given two complex numbers in polar form without converting them to rectangular form first.
We’ve learned everything we need so far for the polar and rectangular forms of complex numbers and numbers in general. It’s time that we test our knowledge by trying out these sample problems below.
Example 1
Review our knowledge of polar coordinates by converting the following rectangular coordinates into polar form.
a. $(-\sqrt{3}, 1)$
b. $(-2, -2\sqrt{3})$
c. $(8, -8)$
Solution
Given a rectangular coordinate, $(x, y)$, we find, $r$, the distance between $(x, y)$ from the origin using the property, $r = \sqrt{x^2 + y^2}$.
The value of $\theta$ can be determined by taking the tangent inverse of $\dfrac{y}{x}$.
Applying this to $(-\sqrt{2}, 1)$, we have the following values of $r$ and $\theta$.
| $\boldsymbol{r}$ | $\boldsymbol{\theta}$ |
| $\begin{aligned}r &= \sqrt{(-\sqrt{3})^2 + (1)^2}\\&=\sqrt{3 + 1}\\&=\sqrt{4}\\&= 2 \end{aligned}$ | $\begin{aligned}\tan \theta &= \dfrac{1}{-\sqrt{3}}\\\theta &= \tan^{-1} \dfrac{1}{-\sqrt{3}}\\&=150^{\circ}, 330^{\circ}\end{aligned}$ |
Since $x$ is negative and $y$ is positive, $\theta$ lies on the second quadrant, so $\theta = 150^{\circ}$. Use $r$ and $\theta$ to write the polar form of the coordinate.
This means that $(-\sqrt{2}, 1)$ is equal to $(2, 150^{\circ})$.
We’ll apply the same process for the two other coordinates to find their polar forms.
| $\boldsymbol{(x, y)}$ | $\boldsymbol{r}$ | $\boldsymbol{\theta}$ | $\boldsymbol{(r, \theta))}$ |
| $(-2, -2\sqrt{3})$ | $\begin{aligned}r &= \sqrt{(-2)^2 + (-2 \sqrt{3})^2}\\&=\sqrt{4 + 12}\\&=\sqrt{16}\\&= 4 \end{aligned}$ | $\begin{aligned}\tan \theta &= \dfrac{-2\sqrt{3}}{-2}\\\theta &= \tan^{-1} \sqrt{3}\\&=240^{\circ}\end{aligned}$ | $(4, 240^{\circ})$. |
| $(8, -8)$ | $\begin{aligned}r &= \sqrt{(8)^2 + (-8)^2}\\&=\sqrt{64 + 64}\\&=\sqrt{128}\\&= 8\sqrt{2} \end{aligned}$ | $\begin{aligned}\tan \theta &= \dfrac{-8}{8}\\\theta &= \tan^{-1} -1\\&=315^{\circ}\end{aligned}$ | $(8\sqrt{2}, 315^{\circ})$ |
Hence, we have the following:
a. $(-\sqrt{3}, 1) =(2, 150^{\circ})$
b. $(-2, -2\sqrt{3}) = (4, 240^{\circ})$
c. $(8, -8) = (8\sqrt{2}, 315^{\circ})$
Example 2
Graph the following complex numbers on one complex plane, then convert them to polar form.
a. $-3+ 3i$
b. $4 + 4\sqrt{3}i$
c.$2\sqrt{3} – 2i$
Solution
When graphing complex numbers of the form, $a + bi$, the point must be $a$ units from the right or left of the vertical axis and $b$ units above or below the horizontal axis. It can also help keep in mind that it’s actually the same as graphing the point $(a, b)$.
- The number $-3 + 3i$ is $3$ units from the left of the vertical axis and $3$ units above the horizontal axis.
- Similarly, $4 + 4\sqrt{3}i$ is $4$ units from the right of the vertical axis and $4\sqrt{3}$ units above the horizontal axis.
- Lastly, we can graph $2\sqrt{3} – 2i$ by plotting a point that is $2\sqrt{3}$ units from the right and $2$ units below the horizontal axis.
Let’s go ahead and graph these values on the complex plane.
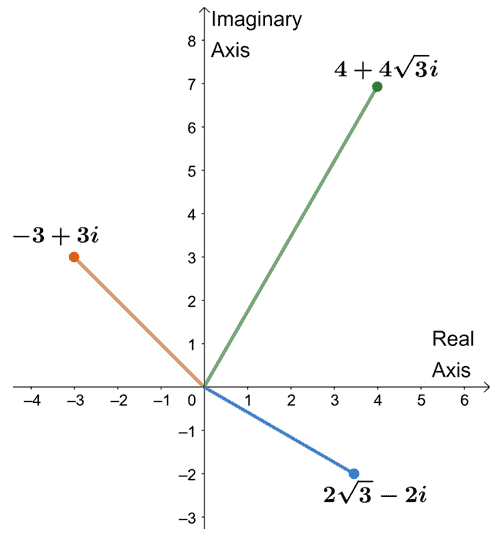
This graph will also guide us in checking whether we have the right value for $r$ and $\theta$ once we convert the three numbers to polar forms.
To convert a complex number, $a + bi$, we have to find its absolute value, $r = \sqrt{a^2 + b^2}$ and angle, $\theta = \tan^{-1} \dfrac{y}{x}$.
Once we have $r$ and $\theta$, we can now write the complex number in its polar form, $r(\cos \theta + i\sin \theta)$ or $r\text{cis} \theta$.
We can first try converting $-3 + 3i$ to polar form by first finding $r$ and $\theta$.
| $\boldsymbol{r}$ | $\boldsymbol{\theta}$ |
| $ \begin{aligned}r&= \sqrt{(-3)^2 + (3)^2}\\&=\sqrt{9 + 9}\\&= \sqrt{18}\\&=3\sqrt{2}\end{aligned}$ | $ \begin{aligned}\tan \theta &= \dfrac{3}{-3}\\\theta&=\tan^{-1} (-1)\\&=135^{\circ}, 315^{\circ} \end{aligned}$ |
Now that we have $r= 3\sqrt{2}$ and $\theta = 135^{\circ}$, let’s convert $-3 + 3i$ to polar form.
$ \begin{aligned}-3 + 3i &= 3\sqrt{2}(\cos 135^{\circ} + i\sin 135^{\circ})\\&=3\sqrt{2} \text{cis}135^{\circ}\end{aligned}$
Let’s apply the same process for the two remaining complex numbers.
| Complex Numbers | $\boldsymbol{r}$ | $\boldsymbol{\theta}$ | $\boldsymbol{r(\cos \theta + i\sin \theta)}$ |
| $4 + 4\sqrt{3}i$ | $ \begin{aligned}r&= \sqrt{(4)^2 + (4\sqrt{3})^2}\\&=\sqrt{16 + 48}\\&= \sqrt{64}\\&=8\end{aligned}$ | $ \begin{aligned}\tan \theta &= \dfrac{4\sqrt{3}}{4}\\\theta&=\tan^{-1} (\sqrt{3})\\&=60^{\circ}\end{aligned}$ | $8(\cos 60^{\circ} + i\sin 60^{\circ})$ |
| $2\sqrt{3} – 2i$ | $ \begin{aligned}r&= \sqrt{(2\sqrt{3})^2 + (2)^2}\\&=\sqrt{12 + 4}\\&= \sqrt{16}\\&=4\end{aligned}$ | $ \begin{aligned}\tan \theta &= \dfrac{-2}{2\sqrt{3}}\\\theta&=\tan^{-1} \left(-\dfrac{1}{\sqrt{3}}\right)\\&=330^{\circ}\end{aligned}$ | $4(\cos 330^{\circ} + i\sin 330^{\circ})$ |
Let’s summarize the results for the three complex numbers:
a. $-3+ 3i = 3\sqrt{2}(\cos 135^{\circ} + i\sin 135^{\circ})$
b. $4 + 4\sqrt{3}I = 8(\cos 60^{\circ} + i\sin 60^{\circ})$
c.$2\sqrt{3} – 2i = 4(\cos 330^{\circ} + i\sin 330^{\circ})$
Example 3
The complex numbers shown below are in their polar forms. Rewrite them so that they are of the form $a + bi$.
a. $4(\cos 30^{\circ} + i\sin 30^{\circ})$
b. $-2\left(\cos \dfrac{3\pi}{4}+ i\sin \dfrac{3\pi}{4}\right)$
c. $-5 \text{cis } 45^{\circ}$
d. $\dfrac{1}{2} \text{cis } \dfrac{3\pi}{2}$
Solution
Rewriting complex numbers from polar forms to their rectangular forms is straightforward.
- Evaluate the trigonometric values based on $\theta$ inside the parenthesis.
- Distribute the absolute value, $r$, to each of the resulting values.
Why don’t we apply this with the first expression? We begin by evaluating $\cos 30^{\circ}$ and $\sin 30^{\circ}$.
$ \begin{aligned}4(\cos 30^{\circ} + i\sin 30^{\circ}) &= 4\left( \dfrac{\sqrt{3}}{2} + \dfrac{1}{2}i\right)\end{aligned}$
Distribute $4$ to each of the trigonometric values to simplify the complex number.
$ \begin{aligned}4\left( \dfrac{\sqrt{3}}{2} + \dfrac{1}{2}i\right) &= 4 \cdot \dfrac{\sqrt{3}}{2} + 4\cdot \dfrac{1}{2}i\\&=2\sqrt{3} + 2i\end{aligned}$
Hence, $4(\cos 30^{\circ} + i\sin 30^{\circ}$ is equivalent to $2\sqrt{3} + 2i$ in rectangular form.
We apply the same process with b, but we’re working with angles in radians this time. Make sure to review your special angles and trigonometric table of values when working with polar forms of complex numbers.
We have the following steps to obtain the polar form of $-2\left(\cos \dfrac{3\pi}{4}+ i\sin \dfrac{3\pi}{4}\right)$.
$\begin{aligned}-2\left(\cos \dfrac{3\pi}{4}+ i\sin \dfrac{3\pi}{4}\right) &= -2\left(-\dfrac{\sqrt{2}}{2}+ \dfrac{\sqrt{2}}{2}i\right)\\&= -2 \cdot -\dfrac{\sqrt{2}}{2} + -2\cdot \dfrac{\sqrt{2}}{2}i\\&=\sqrt{2}-\sqrt{2}i\end{aligned}$
For c, recall that $r\text{cis } \theta$ is just a shorter version of $r(\cos \theta + i\sin \theta)$.
Let’s rewrite $-5 \text{cis } 45^{\circ}$ as $-5 ( \cos 45^{\circ} + i\sin 45^{\circ})$. We then apply similar process to rewrite it in the form $a + bi$: evaluate the cosine and sine of $45^{\circ}$ then distribute $-5$.
$\begin{aligned}-5 \text{cis }45^{\circ} &= -5(\cos 45^{\circ} + i\sin 45^{\circ})\\&= -5\left(\dfrac{\sqrt{2}}{2} + i\dfrac{\sqrt{2}}{2} \right )\\&= -5 \cdot \dfrac{\sqrt{2}}{2} + -5 \cdot \dfrac{\sqrt{2}}{2}i\\&=-\dfrac{5\sqrt{2}}{2} -\dfrac{5\sqrt{2}}{2}i\end{aligned}$
Let’s now work on $\dfrac{1}{2} \text{cis } \dfrac{3\pi}{2}$ by first rewriting this in its expanded form. Evaluate the resulting expression to find the rectangular form of the complex number.
$\begin{aligned}\dfrac{1}{2} \text{cis } \dfrac{3\pi}{2} &= \dfrac{1}{2} \left(\cos \dfrac{3\pi}{2} + i\sin \dfrac{3\pi}{2} \right )\\&= \dfrac{1}{2} [0 + i(-1)]\\&= \dfrac{1}{2}(-i)\\&= -\dfrac{1}{2}i\end{aligned}$
This means that we have the following expressions when the four are converted to rectangular form.
a. $4(\cos 30^{\circ} + i\sin 30^{\circ}) = 2\sqrt{3} + 2i $
b. $-2\left(\cos \dfrac{3\pi}{4}+ i\sin \dfrac{3\pi}{4}\right) = \sqrt{2}-\sqrt{2}i $
c. $-5 \text{cis } 45^{\circ} =-\dfrac{5\sqrt{2}}{2} -\dfrac{5\sqrt{2}}{2}i $
d. $\dfrac{1}{2} \text{cis } \dfrac{3\pi}{2} = -\dfrac{1}{2}i $
Example 4
Find the product of the following pairs of complex numbers. Express your final answer in polar form.
a. $z_1 = 3(\cos 50^{\circ} + i\sin 50^{\circ})$, $z_2 = -6(\cos 20^{\circ} + i\sin 20^{\circ})$
b. $z_1 = -4\left(\cos \dfrac{\pi}{12} + i\sin \dfrac{\pi}{12}\right)$, $z_2 =2\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)$
c. $z_1 = 5(\cos 12^{\circ} + i\sin 12^{\circ})$, $z_2 = -2\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)$,and $z_3 = -3(\cos 15^{\circ} + i\sin 15^{\circ})$
Solution
Recall that given two complex numbers, we can find their product by multiplying the absolute values and adding the two angles.
If we have $z_1 = r_1(\cos \theta_1 + i\sin \theta_1)$ and $z_2 = r_2(\cos \theta_2 + i\sin \theta_2)$, their product can be expressed as $z_1z_2 = r_1r_2[\cos(\theta_1 + \theta_2)+ \sin(\theta_1 + \theta_2)].
This means that the product of $z_1 = 3(\cos 50^{\circ} + i\sin 50^{\circ})$ and $z_2 = -6(\cos 20^{\circ} + i\sin 20^{\circ})$ can be determined using the formula shown above.
$\begin{aligned}z_1z_2&= [3(\cos 50^{\circ} + i\sin 50^{\circ})][-6(\cos 20^{\circ} + i\sin 20^{\circ})]\\&= (3 \cdot -6)[\cos (50^{\circ} + 20^{\circ}) + i\sin(50^{\circ} + 20^{\circ})]\\&=-18(\cos 70^{\circ} + i\sin 70^{\circ})\end{aligned}$
We apply the same process to find the product of the two complex numbers in b. The only difference is that we’re working with radians.
$\begin{aligned}z_1z_2&= \left[-4\left(\cos \dfrac{\pi}{12} + i\sin \dfrac{\pi}{12}\right)\right]\left[2\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)\right]\\&=(-4 \cdot 2) \left[\cos\left(\dfrac{\pi}{12} + \dfrac{\pi}{6}\right) + i\sin\left(\dfrac{\pi}{12} + \dfrac{\pi}{6}\right) \right ]\\&=-8 \left[\cos\left(\dfrac{\pi + 2\pi}{12}\right ) + i\sin\left(\dfrac{\pi + 2\pi}{12}\right ) \right]\\&=-8\left(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4} \right )\end{aligned}$
For the third item, we must make sure all angles are either in degrees or in radians. Since we already have two angles in degrees, it’s faster if we change $\dfrac{\pi}{6}$ to degrees. Hence, we have $z_2 = -2(\cos 30^{\circ} + i\sin 30^{\circ})$.
We will still perform the same process, but we’re working with three pairs of absolute value numbers and angles this time.
$\begin{aligned}z_1z_2z_3 &= [5(\cos 12^{\circ} + i\sin 12^{\circ})]\left[-2\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)\right][-3(\cos 15^{\circ} + i\sin 15^{\circ})]\\&=[5(\cos 12^{\circ} + i\sin 12^{\circ})]\left[-2(\cos 30^{\circ} + i\sin 30^{\circ})\right][-3(\cos 15^{\circ} + i\sin 15^{\circ})]\\&= (5 \cdot -2 \cdot -3)[\cos (12^{\circ} + 30^{\circ} + 15^{\circ}) + i\sin(12^{\circ} + 30^{\circ} + 15^{\circ})]\\&= 30(\cos 57^{\circ} + i\sin 57^{\circ})\end{aligned}$
Hence, we have the following products for a, b, and c.
a. $z_1z_2 = -18(\cos 70^{\circ} + i\sin 70^{\circ})$
b. $z_1z_2 = -8\left(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4} \right )$
c. $z_1z_2z_3 = 30(\cos 57^{\circ} + i\sin 57^{\circ})$
Example 5
Find $\dfrac{z_1}{z_2}$ for each of the given pairs of complex numbers.
a. $z_1 = 8(\cos 60^{\circ} + i\sin 60^{\circ})$, $z_2 = -4(\cos 20^{\circ} + i\sin 20^{\circ})$
b. $z_1 = 12\left(\cos \dfrac{7\pi}{12} + i\sin \dfrac{7\pi}{12}\right)$, $z_2 = 6\left(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4}\right)$
c. $ z_1 = -16(\cos 120^{\circ} + i\sin 120^{\circ})$, $z_2 = -4\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)$
Solution
Recall that given two complex numbers, we can find their quotient by dividing the complex number’s absolute values and finding the difference between the two angles.
If we have $z_1 = r_1(\cos \theta_1 + i\sin \theta_1)$ and $z_2 = r_2(\cos \theta_2 + i\sin \theta_2)$, their quotient can be expressed as $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2}[\cos(\theta_1 – \theta_2)+ \sin(\theta_1 – \theta_2)]$.
Using the formula shown above, we can find the quotient of $z_1 = 8(\cos 60^{\circ} + i\sin 60^{\circ})$ and $z_2 = -4(\cos 20^{\circ} + i\sin 20^{\circ})$.
$\begin{aligned}\dfrac{z_1}{z_2}&= \dfrac{8(\cos 60^{\circ} + i\sin 60^{\circ})}{ -4(\cos 20^{\circ} + i\sin 20^{\circ})}\\&=-\dfrac{8}{4}[\cos(60^{\circ} – 20^{\circ}) + i\sin(60^{\circ} – 20^{\circ})]\\&=-2 (\cos 40^{\circ} + i\sin 40^{\circ})\end{aligned}$
This time, let’s work with radians and subtract the two angles. We’ll apply a similar process of subtracting regular fractions when subtracting the two angles in radians.
$\begin{aligned}\dfrac{z_1}{z_2}&= \dfrac{12\left(\cos \dfrac{7\pi}{12} + i\sin \dfrac{7\pi}{12}\right)}{ 6\left(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4}\right)}\\&= \dfrac{12}{6} \left[\cos \left( \dfrac{7\pi}{12} – \dfrac{\pi}{4} \right )+ i\sin \left( \dfrac{7\pi}{12} – \dfrac{\pi}{4} \right ) \right ]\\&=2 \left[\cos\left( \dfrac{7\pi – 3\pi}{12} \right ) + i\sin\left( \dfrac{7\pi – 3\pi}{12} \right ) \right ]\\&= 2\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3} \right)\end{aligned}$
For the third item, we can either write all the angles in degrees or radians. Since it’s easier to subtract angles in degrees, change $\dfrac{\pi}{6}$ to $30^{\circ}$.
$\begin{aligned}\dfrac{z_1}{z_2}&= \dfrac{-16(\cos 120^{\circ} + i\sin 120^{\circ})}{ = -4\left(\cos \dfrac{\pi}{6} + i\sin \dfrac{\pi}{6}\right)}\\&= \dfrac{-16(\cos 120^{\circ} + i\sin 120^{\circ})}{-4(\cos 30^{\circ} + i\sin 30^{\circ})}\\&= \dfrac{-16}{-4} [\cos(120^{\circ} – 30^{\circ}) + i\sin(120^{\circ} – 30^{\circ})]\\&= 4 (\cos 90^{\circ} + i\sin 90^{\circ})\end{aligned}$
Let’s go ahead and list down the resulting quotients of the three items.
a. $\dfrac{z_1}{z_2} = -2 (\cos 40^{\circ} + i\sin 40^{\circ}) $
b. $\dfrac{z_1}{z_2} = 2\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3} \right) $
c. $\dfrac{z_1}{z_2} = 4 (\cos 90^{\circ} + i\sin 90^{\circ})$
Example 6
Given that $z_ 1 = 4\text{cis } 60^{\circ}$, $z_2 = -6(\cos 30^{\circ} + i\sin 30^{\circ})$, and $z_3 = -12 \left(\cos \dfrac{\pi}{4} + i \sin \dfrac{\pi}{4}\right)$, find the value of the following expressions:
a. $z_1 \cdot z_2$ (Write your answer in the rectangular form)
b. $\dfrac{z_1}{z_3} $
c. $ \dfrac{z_1 \cdot z_ 3}{z_2}$
Solution
The first item requires us to multiply $z_1$ and $z_2$. Let’s first rewrite $z_1$ as $4(\cos 60^{\circ} + i\sin 60^{\circ})$. Find their product by adding $4$ and $-6$ the finding the cosine and sine of $(60^{\circ} + 30^{\circ})$.
$\begin{aligned}z_1 \cdot z_2 &= [4(\cos 60^{\circ} + i\sin 60^{\circ} )] \cdot [-6(\cos 30^{\circ} + i\sin 30^{\circ})]\\&= (4 \cdot -6)[\cos ( 60^{\circ} + 30^{\circ}) + i\sin ( 60^{\circ} + 30^{\circ})]\\&=-24 (\cos 90^{\circ} + i\sin 90^{\circ})\end{aligned}$
The product is still in polar form, so if we want a rectangular form as our final answer, let’s evaluate $\cos 90^{\circ}$ and $\sin 90^{\circ}$ then distribute $-24$ to each of the values.
$\begin{aligned}z_1 \cdot z_2 &= -24 (\cos 90^{\circ} + i\sin 90^{\circ})\\&= -24(0 + i)\\&= -24i\end{aligned}$
Next, we want to find the quotient of $z_1$ and $z_3$. To do so, we can divide $4$ by $-12$, then subtract the two angles, then find the cosine and sine of the difference.
But before we do, let’s convert $\dfrac{\pi}{4}$ from $z_3$ to degrees since it’s easier to find the difference of whole numbers.
$\begin{aligned}\dfrac{z_1}{z_3}&= \dfrac{4(\cos 60^{\circ} + i\sin 60^{\circ} )}{-12(\cos 45^{\circ} + i\sin 45^{\circ})}\\&= \dfrac{4}{-12} [\cos(60^{\circ} – 45^{\circ}) + i\sin (60^{\circ} – 45^{\circ})]\\&= -\dfrac{1}{3}(\cos 15^{\circ} + i\sin 15^{\circ})\end{aligned}$
To find the value of $\dfrac{z_1 \cdot z_ 3}{z_2}$, let’s begin by simplifying the numerator. Again, since it’s easier to add angles in degrees, we’ll use $z_3 =-12(\cos 45^{\circ} + i\sin 45^{\circ})$.
$\begin{aligned}\dfrac{z_1 \cdot z_3}{z_2}&= \dfrac{(4\text{cis } 60^{\circ}) \cdot [-12(\cos 45^{\circ} + i\sin 45^{\circ})]}{-6(\cos 30^{\circ} + i\sin 30^{\circ})}\\\\z_1 \cdot z_3 &= [4 \cos 60^{\circ} + i\sin60^{\circ}][-12(\cos 45^{\circ} + i\sin 45^{\circ})]\\&= (4 \cdot -12)[\cos(60^{\circ} + 45^{\circ}) + i\sin(60^{\circ} + 45^{\circ})]\\&= -48 (\cos 105^{\circ} + i \sin 105^{\circ}) \end{aligned}$
Replace the numerator with $-48 (\cos 105^{\circ} + i \sin 105^{\circ})$ then divide this by $z_2 = -6(\cos 30^{\circ} + i\sin 30^{\circ})$. To divide the two values, we divide $-48$ by $-8$ and find the cosine and sine of $105^{\circ} + 30^{\circ}$.
$\begin{aligned}\dfrac{z_1 \cdot z_3}{z_2}&= \dfrac{-48 (\cos 105^{\circ} + i \sin 105^{\circ})}{-6(\cos 30^{\circ} + i\sin 30^{\circ})}\\&=\dfrac{-48}{-6} [\cos(105^{\circ} – 30^{\circ}) + i\sin (105^{\circ} – 30^{\circ})]\\&= 8 (\cos 75 + i \sin 75^{\circ} ) \end{aligned}$
We can list down the values of $z_1 \cdot z_2$, $\dfrac{z_1}{z_3}$, and $ \dfrac{z_1 \cdot z_ 3}{z_2}$.
a. $z_1 \cdot z_2 = -24i $
b. $\dfrac{z_1}{z_3} = -\dfrac{1}{3}(\cos 15^{\circ} + i\sin 15^{\circ})$
c. $ \dfrac{z_1 \cdot z_ 3}{z_2} = 8 (\cos 75 + i \sin 75^{\circ} )$
Example 7
Given that $z_ 1 = -2 – 2i$, $z_2 = 4\sqrt{3} + 4i$, and $z_3 = 8 – 8\sqrt{3}i$, find the value of the following expressions:
a. $z_1 \cdot z_2$
b. $(z_3)^2$
c. $ \dfrac{z_1 \cdot z_ 2}{(z_3)^2}$
Write your answers in polar form.
Solution
Since we want the final answers to be in polar form, it is much easier to rewrite $z_1$, $z_2$, and $z_3$ in the polar form first.
- For each complex number, we first find the absolute value of the complex number using $r = \sqrt{a^2 + b^2}$, where $a$ represents the real number parts and $b$ represents the imaginary number parts.
- We can then find the angle or argument of the complex number using $\tan^{-1} \dfrac{b}{a}$.
- Write each complex number in the form of $r(\cos \theta + i\sin \theta)$.
Let’s summarize our calculations in a table.
| $\boldsymbol{a + bi}$ | $\boldsymbol{r}$ | $\boldsymbol{\theta}$ | $\boldsymbol{ r(\cos \theta + i\sin \theta)}$ |
| $z_ 1 = -2 – 2i$ | $\begin{aligned} r&= \sqrt{(-2)^2 + (-2)^2}\\&= 2\sqrt{2} \end{aligned}$ | $\begin{aligned} \theta &= \tan^{-1} \dfrac{-2}{-2}\\&= \tan^{-1} 1\\&= 225^{\circ} \end{aligned}$ | $2\sqrt{2}(\cos 225^{\circ} + i\sin 225^{\circ})$ |
| $z_2 = 4\sqrt{3} + 4i$ | $\begin{aligned} r&= \sqrt{(4\sqrt{3})^2 + (4)^2}\\&= \sqrt{48 + 16}\\&=\sqrt{64}\\&= 8\end{aligned}$ | $\begin{aligned} \theta &= \tan^{-1} \dfrac{4}{4\sqrt{3}}\\&= \tan^{-1} \dfrac{1}{\sqrt{3}}\\&= 30^{\circ} \end{aligned}$ | $8(\cos 30^{\circ} + i\sin 30^{\circ})$ |
| $z_3 = 8 – 8\sqrt{3}i$ | $\begin{aligned} r&= \sqrt{(8\sqrt{3})^2 + (8)^2}\\&= \sqrt{192 + 64}\\&=\sqrt{256}\\&= 16\end{aligned}$ | $\begin{aligned} \theta &= \tan^{-1} \dfrac{-8\sqrt{3}}{8}\\&= \tan^{-1} -\sqrt{3}\\&= 300^{\circ} \end{aligned}$ | $16(\cos 300^{\circ} + i\sin 300^{\circ})$ |
Let’s begin by finding $z_1 \cdot z_2$ by multiplying $2\sqrt{2}$ and $8$ then finding the cosine and sine of $225^{\circ} + 30^{\circ}$.
$\begin{aligned}z_1 \cdot z_2 &= [2\sqrt{2}(\cos 225^{\circ} + \sin 225^{\circ})]\cdot[8(\cos 30^{\circ} + \sin 30^{\circ})]\\&=(2\sqrt{2} \cdot 8) [\cos (225^{\circ} + 30^{\circ}) + i\sin (225^{\circ} + 30^{\circ})] \\&= 16\sqrt{2}(\cos 255^{\circ} + i\sin 255^{\circ})\end{aligned}$
We can express $(z_3)^2$ as $z_3 \cdot z_3$ then find the product of $16(\cos 300^{\circ} + \sin 300^{\circ})$ and itself.
$\begin{aligned}z_3 \cdot z_3 &= [16(\cos 300^{\circ} + i\sin 300^{\circ})][16(\cos 300^{\circ} + i\sin 300^{\circ})]\\&= (16 \cdot 16)[\cos(300^{\circ} + 300^{\circ}) + i\sin (300^{\circ} + 300^{\circ})]\\&= 256(\cos 600^{\circ} + i\sin 600^{\circ})\end{aligned}$
We can also rewrite $\cos 600^{\circ}$ and $\sin 600^{\circ}$ as $\cos (600^{\circ} – 360^{\circ}) = \cos 240^{\circ}$ and $\sin (600^{\circ} – 360^{\circ}) = \sin 240^{\circ}$.
Hence, we have $256 (\cos 240^{\circ}+ \sin 240^{\circ})$.
We can use our results from part a and b to find $ \dfrac{z_1 \cdot z_ 2}{(z_3)^2}$. Once we replace the numerator and denominator with $16\sqrt{2}(\cos 255^{\circ} + i\sin 255^{\circ})$ and $256 (\cos 240^{\circ}+ \sin 240^{\circ})$, respectively, we can then simplify the expression as shown below.
$\begin{aligned}\dfrac{z_1 \cdot z_ 2}{(z_3)^2} &= \dfrac{16\sqrt{2}(\cos 255^{\circ} + i\sin 255^{\circ})}{256 (\cos 240^{\circ}+ \sin 240^{\circ})}\\&= \dfrac{16\sqrt{2}}{256}[\cos(255^{\circ} – 240^{\circ}) + i\sin(255^{\circ} – 240^{\circ})]\\&= \dfrac{\sqrt{2}}{16} (\cos 15^{\circ} + i\sin 15^{\circ}) \end{aligned}$
Hence, we have the values of $z_1 \cdot z_2$, $(z_3)^2$, and $ \dfrac{z_1 \cdot z_ 2}{(z_3)^2}$ in polar form as shown below:
a. $z_1 \cdot z_2 = 16\sqrt{2}(\cos 255^{\circ} + i\sin 255^{\circ})$
b. $(z_3)^2 = 256 (\cos 240^{\circ}+ \sin 240^{\circ})$
c. $ \dfrac{z_1 \cdot z_ 2}{(z_3)^2} = \dfrac{\sqrt{2}}{16} (\cos 15^{\circ} + i\sin 15^{\circ}) $
Example 8
Let’s say, we have $z = r(\cos \theta + i \sin \theta)$. Find the expressions of the following in terms of $r$ and $\theta$.
a. $z^2$
b. $z^3$
c. $z^4$
d. $z^n$
Solution
We can rewrite $z^2$ as $z \cdot z = [r(\cos \theta + i \sin \theta)] \cdot [r(\cos \theta + i \sin \theta)]$. This means that we simply multiply $r$ to itself and find the cosine and sine values of $\theta + \theta$.
$\begin{aligned}z^2 &= [r (\cos \theta + i\sin \theta)][r (\cos \theta + i\sin \theta)]\\&=(r \cdot r)[\cos(\theta + \theta) + i\sin(\theta + \theta)]\\&=r^2(\cos 2\theta + i\sin 2\theta) \end{aligned}$
To find $z^3$, we multiply $z$ to the result of $z^2$. Hence, we have the calculations as shown below.
$\begin{aligned}z^3 &= z \cdot z^2\\&= [r(\cos \theta + i\sin \theta)][r^2(\cos 2\theta + i\sin 2\theta) ]\\&= (r \cdot r^2)[\cos (\theta + 2\theta) + i\sin(\theta + 2\theta)]\\&=r^3(\cos 3\theta + i\sin 3\theta)\end{aligned}$
Notice a pattern yet? Let’s work on $z^4$ so you one more item to observe. Again, we simply multiply $z = r(\cos \theta + i \sin \theta)$ to the $z^3 = r^3(\cos 3\theta + i\sin 3\theta)$.
$ \begin{aligned}z^4 &= z \cdot z^3\\&= [r(\cos \theta + i\sin \theta)][r^3(\cos 3\theta + i\sin 3\theta) ]\\&= (r \cdot r^3)[\cos (\theta + 3\theta) + i\sin(\theta + 3\theta)]\\&=r^4(\cos 4\theta + i\sin 4\theta)\end{aligned}$
Why don’t we write down the four results first and find a pattern?
$ \begin{aligned}z^1 &=r^1(\cos 1\theta + i\sin 1\theta)\\z^2 &=r^2(\cos 2\theta + i\sin 2\theta)\\z^3 &=r^3(\cos 3\theta + i\sin 3\theta)\\z^4 &=r^4(\cos 4\theta + i\sin 4\theta)\end{aligned}$
We can see that when $z$ is raised a power say, $n$, we can multiply $r$ by $n$ then multiply the $\theta$ by $n$.
This means that $z^n$ can be expressed as $r^n (\cos n\theta + i\sin n\theta)$. This is actually a property of complex numbers, and we’ll divide further into this topic when we learn about DeMoivre’s Theorem.
For now, let’s write down the results we have for the four items:
a. $z^2 = r^2 (\cos 2\theta + i\sin 2\theta) $
b. $z^3 = r^3 (\cos 3\theta + i\sin 3\theta) $
c. $z^4 = r^4 (\cos 4\theta + i\sin 4\theta) $
d. $z^n = r^n (\cos n\theta + i\sin n\theta) $
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
