JUMP TO TOPIC
Position Vector – Explanation and Examples
We can use a position vector to tell us the location of one object relative to another. Specifically, a position vector is:
“A vector which indicates the location or position of a given point with respect to an arbitrary reference point such as the origin.”
In this topic, we will discuss the following aspects of position vectors:
- What is a Position Vector?
- How to Find the Position Vector
What is a Position Vector?
Often, vectors that start at the origin and terminate at any arbitrary point are called position vectors. These are used to determine the position of a point with reference to the origin.
The direction of the position vector points from the origin towards the given point. In the c\Cartesian coordinate system, if point O is the origin and Q is some point (x1, y1), then the position vector directed from point O to point Q is represented as OQ. In three-dimensional space, if O = (0,0,0) and Q = (x1, y1, z1), then the position vector r of point Q is represented is:
r = x1i + y1j + z1k
Let’s suppose we have two vectors, A and B, with position vectors a = (2,4) and b = (3, 5) respectively. We can then write the coordinates of the vectors A and B as:
A = (2,4), B = (3, 5)
How to Find the Position Vector
Before determining the position vector of a point, we first need to determine the coordinates of that point. Let’s suppose we have two points, M and N, where M = (x1, y1) and N = (x2, y2). Next, we want to find the position vector from point M to point N, the vector MN. To determine this position vector, we subtract the corresponding components of M from N:
MN = (x2-x1, y2-y1)
Position Vector Formula
Using the information above, we can generalize a formula that will determine a position vector between two points if we knew the position of the points in the xy-plane.
For example, consider a point P, which has the coordinates (xk, yk) in the xy-plane, and another point Q, which has the coordinates (xk+1, yk+1). The formula to determine the position vector from P to Q is:
PQ = ((xk+1)-xk, (yk+1)-yk)
Remember the position vector PQ refers to a vector that starts at the point P and ends at the point Q. Similarly, if we want to find the position vector from the point Q to the point P, we can write:
QP = (xk – (xk+1), yk – (yk+1))
Examples
In this section, we will discuss some position vector example problems and their step-by-step solutions. This will help to build a deeper understanding of position vectors.
Example 1
Given two points A = (-4, 6) and B = (5, 12), determine the position vector AB. Then, compute the magnitude of the vector AB.
Solution
Given two points in the xy-coordinate system, we can use the following formula to find the position vector AB:
AB = (x2-x1, y2-y1)
Where x1, y1 represents the coordinates of point A and x2, y2 represent the point B coordinates. Thus, by simply putting the values of points A and B in the above equation, we can find the position vector AB:
AB = (5-(-4), 12-6)
AB = ((5+ 4), 12-6)
AB = (9, 6)
Thus, the position vector AB is equivalent to a vector that starts at the origin and is directed to a point 9 units to the right along the x-axis and 6 units upward along the y-axis.
Next, we determine the magnitude of the position vector as follows:
|AB| = √9^2 + 6 ^2
|AB| = √81 + 36
|AB| = √117
|AB| = 3√13
Example 2
Given two points A = (-4, 6) and B = (5, 12), determine the position vector BA. Then, compute the vector BA‘s magnitude and describe the relationship between the position vector AB and the position vector BA.
Solution
Given two points in the xy-coordinate system, we can use the following formula to find the position vector BA:
BA = (x1-x2, y1-y2)
Where x1, y1 represents the coordinates of point A and x2, y2 represent the point B coordinates. Note that the position vector BA represents a vector directed from point B towards point A. It is different from the position vector AB, which is directed from A to B. Thus, by simply putting the values of points A and B in the above equation, we can find the position vector BA:
BA = (-4-5), 6-12)
BA = (-9, -6)
Thus, the position vector BA is equivalent to a vector that starts at the origin and is directed to a point 9 units to the left along the x-axis and 6 units downward along the y-axis.
Next, we determine the magnitude of the position vector:
|BA| = √(-9)^2 + (-6) ^2
|BA| = √81 + 36
|BA| = √117
|BA| = 3√13
Recall that in the first example, we found the position vector AB for the same points and, in this example, we determined the position vector BA. The two position vectors have the same magnitude. Since they have opposite directions, the relationship between the two is:
BA = -1*(9, 6)
BA = -1*AB
BA = –AB
Thus, the two position vectors are parallel to each other and are opposite to each other. That is, they are the negatives of each other.
Example 3
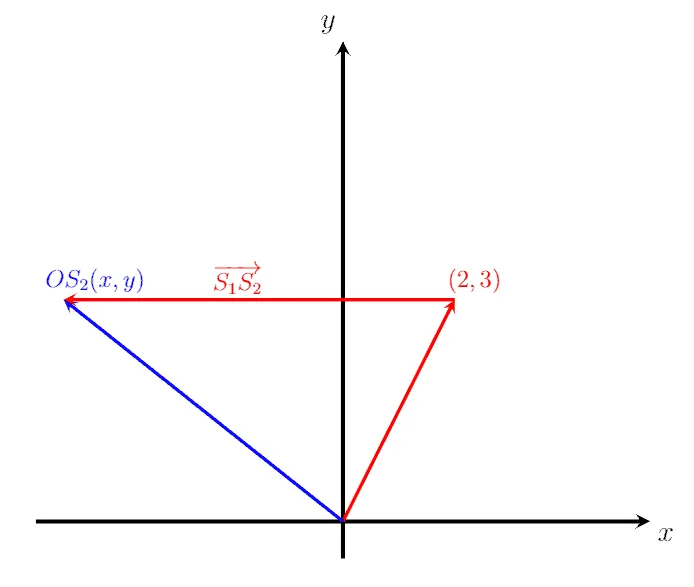
Given that the position vector of a point, S1, is OS1 = (2, 3), and that the vector S1S2 = (-3, 6), determine the position vector of the point S2, OS2.
Solution
First, we plot the vector OS1 with its initial point at the origin, (0,0), and its endpoint at (2,3). We also plot the vector OS2, which starts at the origin and ends at the point S2. We will designate the unknown position of S2 with the arbitrary coordinate points (x,y). Since we know the position vector S1S2 and we know that it gives a relationship between S1 and S2, we can also draw S1S2. It is a vector directed whose initial point is at S1 and which is directed three units to the left and six units upward. It is obvious from the image below that we have a triangle, 0S1S2. Thus, we can now use the triangle law (or head-to-tail rule) of vector addition to determine the coordinates of point S2 as follows:
S1S2 = OS1 + OS2
OS2 = S1S2 – OS1
By putting the given values into this equation, we get:
OS2 = (-3, 6) – (2, 3)
OS2 = (-3, 6) + (-2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Thus, OS2=(-5, 3) is the position vector for the point S2.
Example 4
Given the two points M = (4, m) and Q = (-n, -3), determine the position vector QM.
Solution
Given two points in the xy-coordinate system, we can use the following formula to determine the position vector Q:
QM = (-n-4, -3-m).
Since we do not know the coordinates of QM or the values of n and m, we cannot simplify the equation.
Example 5
Given a point q = (-10, 5, 3), determine the position vector of point q, R. Then, determine the magnitude of R.
Solution
Given the point q, we can determine its position vector:
R = -10i + 5j -3k.
To determine its magnitude, we use the following equation:
|R| = √(-10)^2 + (5)^2 + (-3)^2
|R| = √100 + 25 + 9
|R| = √100 + 25 + 9
|R| = √134
Example 6
Given the points, c = 5i + 6j +3k and d = 2i +5j – 2k in the orthogonal system, determine the position vector between these two points, CD.
Solution
Given the two points, we can use the following formula to determine the position vector CD:
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Practice Questions
- Let u = (-1, 4) and v = (2, 5). Determine the position vector represented by UV.
- Let u = (-1, 4) and v = (2, 5). Determine the position vector represented by VU.
- Let v = (3, 5) and VM = (-6, 3). Find the position vector of the point m.
- Given b = (3,2,5), determine its position vector, R. Then, find the length of the vector
- Let a vector AB start at a = (1, 2) and end at b = (2, 3). Determine its position vector and its length.
- Let a vector OB start at o = (0,0) and end at b = (-2, 6). Determine its position vector.
Answers
- UV = (3,1). The direction of UV is 3 units to the right along the x-axis and 1 unit up.
- VU = (-3,-1). The direction of VU is 3 units to the left along the x-axis and 1 unit down. The two vectors UV and VU, are opposite in direction.
- The position vector of the point m can be given OM = (-9, -2)
- R = 3i + 2j + 5k is the position vector, and its length is |R| = √38
- The position vector is AB = (1,1), and its length is |AB| = √2
- The position vector is OB = (-2,6), and its length is |OB| = √40