Probability Of Multiple Events – Conditions, Formulas, and Examples
The probability of multiple events is an interesting topic discussed in mathematics and statistics. There are instances where we’re observing multiple events and want particular results – when this happens, knowing how to calculate the probability of multiple events comes in handy.The probability of multiple events helps us measure our chances of getting the desired outcomes when two or more vents are occurring. The measured probability will heavily depend on whether the given events are independent or dependent.Seeing that this is a more complex topic than the earlier topics of probability, make sure to refresher your knowledge on the following:- Understand how we calculate probabilities of a single event.
- Review what complementary probabilities are.
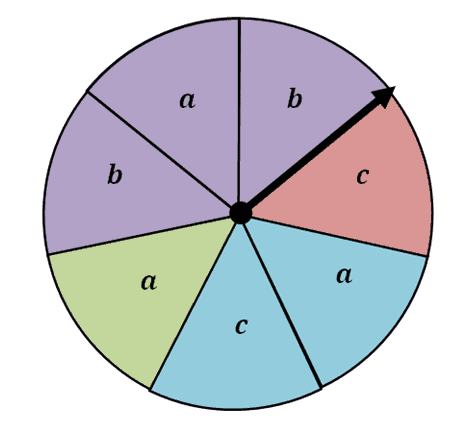Speaking of spinners, why don’t we observe the image shown above? From this, we can see that the spinner is divided into seven regions and distinguished by either the region’s colors or labels. Here are examples of multiple events we can check from the spinners:- Finding the probability of spinning a violet or an $a$.
- Finding the probability of spinning a blue or a $b$.
- Dependent events (also known as conditional events) are events where a given event’s outcomes are affected by the remaining events’ outcomes.
- Independent events are events where one event’s outcomes are not affected by the rest of the events’ outcomes.
Dependent Events | Independent Events |
| Drawing two balls consecutively from the same bag. | Finding one ball each from two bags. |
| Picking two cards without replacement. | Picking a card and rolling a die. |
| Buying more lottery tickets to win the lottery. | Winning the lottery and seeing your favorite show on a streaming platform. |
Knowing how to distinguish these two events will be extremely helpful when we learn how to evaluate the probabilities of two or more events that occur together. How to find the probability of multiple events? We’ll be using different approaches when finding the probability of multiple events occurring together depending on whether these events are dependent, independent, or mutually exclusive. Finding the Probability of Independent Events\begin{aligned}P(A \text{ and } B) &=P(A) \times P(B)\\P(A \text{ and } B \text{ and } C\text{ and }…) &=P(A) \times P(B) \times P(C) \times … \end{aligned}When we’re working with independent events, we can calculate the probability occurring together by multiplying the respective probabilities of the events occurring individually.Let’s say we have the following objects handy:- A bag that contains $6$ red and $8$ blue chips.
- A coin is in your purse.
- A deck of cards is on your office table.
Event | Symbol | Probability |
Getting a red chip | $P(r)$ | $P(r) = \dfrac{6}{14} = \dfrac{5}{7}$ |
Tossing the coin and get a tails | $P(t)$ | $P(t) = \dfrac{1}{2}$ |
Drawing a hearts | $P(h)$ | $P(h) = \dfrac{13}{52} = \dfrac{1}{4}$ |
\begin{aligned}P(r \text{ and }t \text{ and }h)&= P(r) \cdot P(t)\cdot P(h)\\&= \dfrac{5}{7}\cdot \dfrac{1}{2} \cdot \dfrac{1}{4}\\&= \dfrac{5}{56} \end{aligned} | ||
- The probability of getting a jack on the first draw – we still have $52$ cards here.
- The probability of getting a second jack on the second draw (we now have $3$ jacks and $51$ cards).
- The third event is getting a third jack for the third row – $2$ jacks left and $50$ cards on the deck.
Event | Symbol | Probability |
Drawing a jack the first time | $P(J_1)$ | $\dfrac{4}{52}= \dfrac{1}{13}$ |
Drawing a jack the second time | $P(J_2|J_1)$ | $\dfrac{4 -1}{52 -1} = \dfrac{1}{17}$ |
Drawing a jack the third time | $P(J_3|J_1 \text{ and } J_2)$ | $\dfrac{3-1}{51 -1} = \dfrac{1}{25}$ |
\begin{aligned}P(J_1) \times P(J_2 \text{ given } J_1)\times P(J_3 \text{ given } J_2\text{ and }J_1)&=P(J_1) \times P(J_2|J_1)\times P(J_3|J_1 \text{ and } J_2)\\&=\dfrac{4}{52}\cdot\dfrac{3}{51}\cdot\dfrac{2}{50}\\&= \dfrac{1}{13}\cdot \dfrac{1}{17}\cdot \dfrac{1}{25}\\&= \dfrac{1}{5525} \end{aligned} | ||
Type of Event | Formula for the Probability |
| Mutually Inclusive | $P(A \text{ or } B) = P(A) + P(B) – P(A \text{ and } B)$ |
| Mutually Exclusive | $P(A \text{ or } B) = P(A) + P(B)$ |
Event | Symbol | Probability |
Drawing a pink cube in the first draw | $P(C)$ | $P(C_1) = \dfrac{6}{24}= \dfrac{1}{4}$ |
Drawing a purple cube in the second draw | $P(C_2)$ | $P(C_2) = \dfrac{10}{24}= \dfrac{5}{12}$ |
Drawing another pink cube in the third draw | $P(C_3)$ | $P(C_3) = \dfrac{6}{24}= \dfrac{1}{4}$ |
\begin{aligned}P(C_1 \text{ and }C_2\text{ and }C_3)&= P(C_1) \cdot P(C_2)\cdot P(C_3)\\&= \dfrac{1}{4}\cdot \dfrac{5}{12} \cdot \dfrac{1}{4}\\&= \dfrac{5}{192} \end{aligned} | ||
- For the first selection, we have $40$ members and $30$ nonfiction readers.
- For the second selection, we now have $40 -1 = 39$ members and $30- 1= 29$ nonfiction readers.
- Hence, for the third, we have $38$ members and $28$ nonfiction readers.
Event | Symbol | Probability |
Randomly selecting a nonfiction reader | $P(N_1)$ | $\dfrac{30}{40}= \dfrac{3}{4}$ |
Selecting another nonfiction reader | $P(N_2|N_1)$ | $\dfrac{29}{39}$ |
Selecting a nonfiction reader the third time | $P(N_3|N_1 \text{ and } N_2)$ | $\dfrac{28}{38} = \dfrac{14}{19}$ |
\begin{aligned}P(N_1) \times P(N_2 \text{ given } N_1)\times P(N_3 \text{ given }N_2\text{ and }N_1)&=P(N_1) \times P(N_2|N_1)\times P(N_3|N_1 \text{ and } N_2)\\&=\dfrac{30}{40}\cdot\dfrac{29}{39}\cdot\dfrac{28}{38}\\&= \dfrac{3}{4}\cdot \dfrac{29}{39}\cdot \dfrac{14}{19}\\&= \dfrac{203}{494} \end{aligned} | ||
| Color $\rightarrow$Label $\downarrow$ | Violet | Green | Red | Blue | Total |
$a$ | $1$ | $1$ | $0$ | $1$ | $3$ |
$b$ | $2$ | $0$ | $0$ | $0$ | $2$ |
$c$ | $0$ | $0$ | $1$ | $1$ | $2$ |
Total | $3$ | $1$ | $1$ | $2$ | $7$ |
- There are $3$ violet regions and $3$ regions labelled $a$.
- There is a $1$ region where it’s both violet and labeled $a$.
