Probability With Replacement – Explanation & Examples

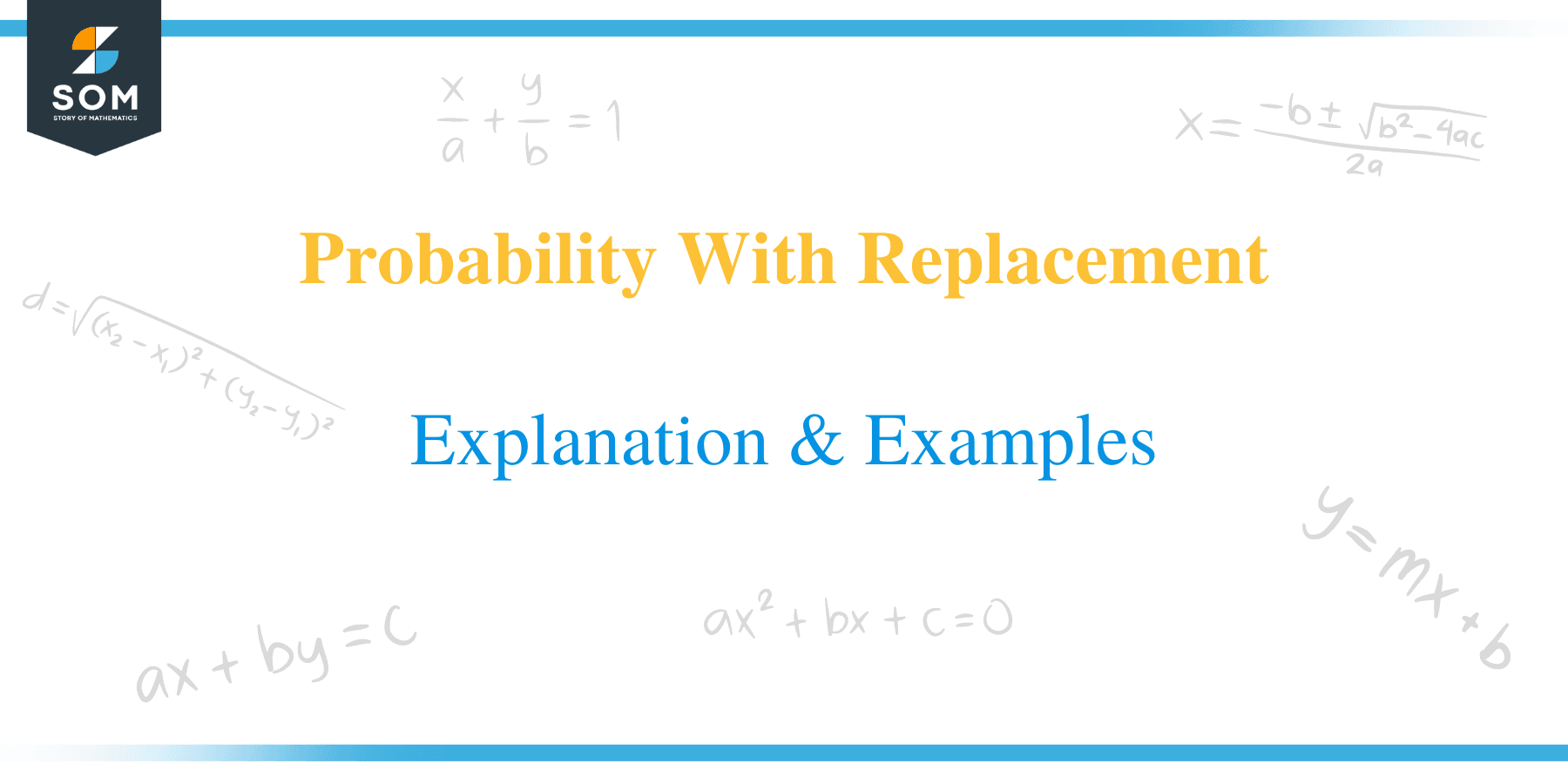To understand probability with replacement, it will be helpful to refresh the following topics:

1. Basics of probability theory.
2. Independent events.
3. Tree diagrams.

After reading this article, you should be able to:

1. Understand what probability with replacement means.
2. Difference between probability with and without replacement.
3. Calculate probability with replacement using basic probability theory.
4. Calculate probability with replacement using tree diagrams.

What does probability with replacement mean

To understand what “probability with replacement” means, let’s start with an example. Suppose we have a box that contains 3 orange balls and 2 blue balls. We are asked to draw two balls, one at a time. Now, what is the probability that both balls are orange?

Before we answer this question, note that there are two ways we can perform this experiment:

Method 1 (With replacement):

1. Draw a ball; it could be blue or orange.
2. Replace the ball from the first draw. So after replacement, the box again contains 3 orange and 2 blue balls.
3. Draw another ball that could again be either blue or orange.

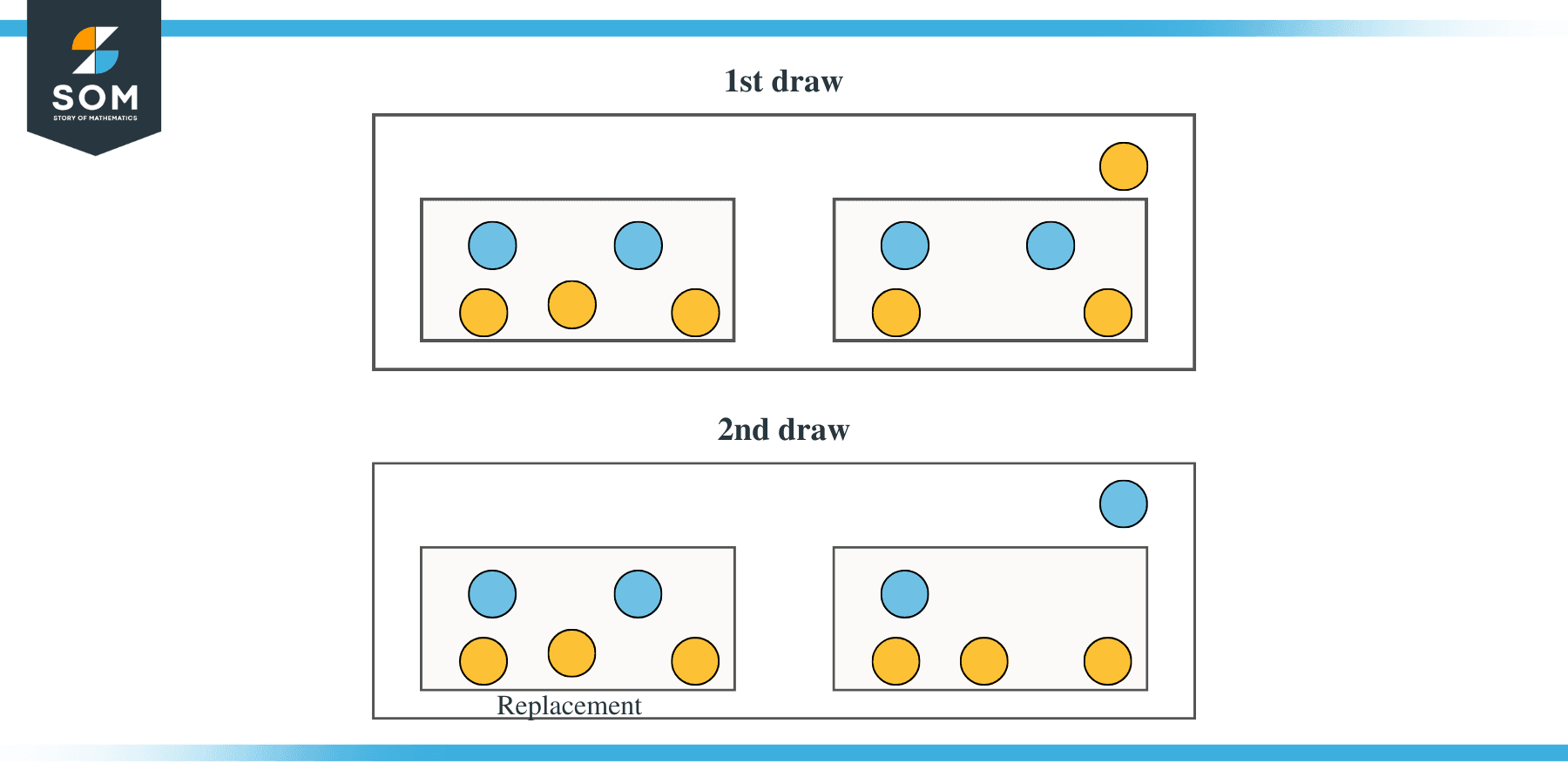
Method 2 (Without replacement):

1. Draw a ball, and it could be blue or orange.
2. Do not replace the ball from the first draw and draw another ball that could again be either blue or orange.

From the above example, we note that “probability with replacement” refers to calculating such events’ probabilities. We have a collection of objects, and we sample from the collection k-times. Each time we sample, we replace the sampled object in the collection.

Probability with replacement and independence:

In probability theory, two events are said to be independent if one event’s outcome does not affect the probability of the other event. For example, if I toss a coin two times, the first toss (Head or Tail) outcome does not affect the probability of the outcome of the second toss. Similarly, the outcome of the second toss does not affect the first toss in any manner. Hence, these two events are said to be independent.

The draws in probability with replacement are independent events. For instance, we note from the example above that we were doing the first draw, and there were 3 orange and 2 blue balls in the box. When we were doing the second draw, again, there were 3 orange and 2 blue balls in the box. The first draw did not affect the second draw and vice versa.

In contrast, in Method 2, i.e., without replacement, the first draw will change the number of either the orange or the blue balls. So the outcome of the second draw is dependent on the first draw when sampling without replacement.

How to calculate Probability with replacement:

Now let’s try to answer the question we asked in the example above, i.e., what is the probability that both balls are orange? To answer that, we first need to know the probability of drawing a orange ball in each draw.

Let

Event1  = First ball is orange, and

Event2 = Second ball is orange

As there are 3 orange balls (let’s call them O1, O2, O3) and 2 blue balls (let’s call them B1 and B2) and we are equally likely to draw any one of them, hence

$P(\textrm{Event1}) = \textrm{number of orange balls}/ \textrm{total number of balls}$

$\qquad \qquad \quad= 3/5$.

In the second draw, we again have three 3 orange and 2 blue balls, so

$P(\textrm{Event2}) = 3/5$.

Remember that when two events are independent, then $P(\textrm{Event1 and Event2}) = P(\textrm{Event1}) \times P(\textrm{Event2})$.  So the probability that both balls are orange is given as

$P(\textrm{Event1 and Event2}) = 3/5 \times 3/5 = 9/25$.

Finding probabilities of some related events:

No orange balls

Let us suppose we are interested in finding the probability that no orange ball is drawn. We know from basic probability theory that if an event’s probability is P, then the probability that the event does not occur is 1-P. So,

$ P(\textrm{first ball is not orange}) = 1 – P( \textrm{first ball is orange}) = 1 – 3/5 = 2/5$.

Similarly,

$P(\textrm{Second ball is not orange}) = 1 – P( \textrm{Second ball is orange}) = 1 – 3/5 = 2/5$.

Finally, due to replacement, both draws are independent and hence

$P(\textrm{Both balls are not orange}) = 2/5 \times 2/5 = 4/25$.

At-least one orange ball:

Another related example is to find the probability of drawing at-least one orange ball. Using the above notation, we are interested in P(Event1 or Event2). Note that or in this context is the logical-OR which means either Event1 or Event2 or both.  From basic axioms of probability, we know that

$P(\textrm{Event1 or Event2}) = P(\textrm{Event1}) + P(\textrm{Event2}) – P(\textrm{Event1 and Event2})$

$= 3/5 + 3/5 – 9/25$

$= 21/25$

Formula for Probability with replacement:

Probability with replacement appears in various forms, and there is no simple formula that applies to all situations. To keep the discussion simple, we describe formulas for a simple example scenario.

Let us suppose, we have a collection of  2 different items. Let’s call them $c_1$ and  $c_2$. Let $c_1$ appears $i$-times and $c_2$ appears $j$-times, in the collection. We sample the collection $k$-times. Let $N=i+j$.

$P(c_1 \textrm{ appears k-times}) = \left(\frac{i}{N}\right)^k$.

$P(c_1 \textrm{ does not appear in any draw}) = \left(1 – \frac{i}{N}\right)^k = \left(\frac{j}{N}\right)^k = P(c_2 \textrm{ appears k-times})$.

$P(c_1 \textrm{ appeasrs atleast once}) = 1-\left (1 – \frac{i}{N}\right)^k$.

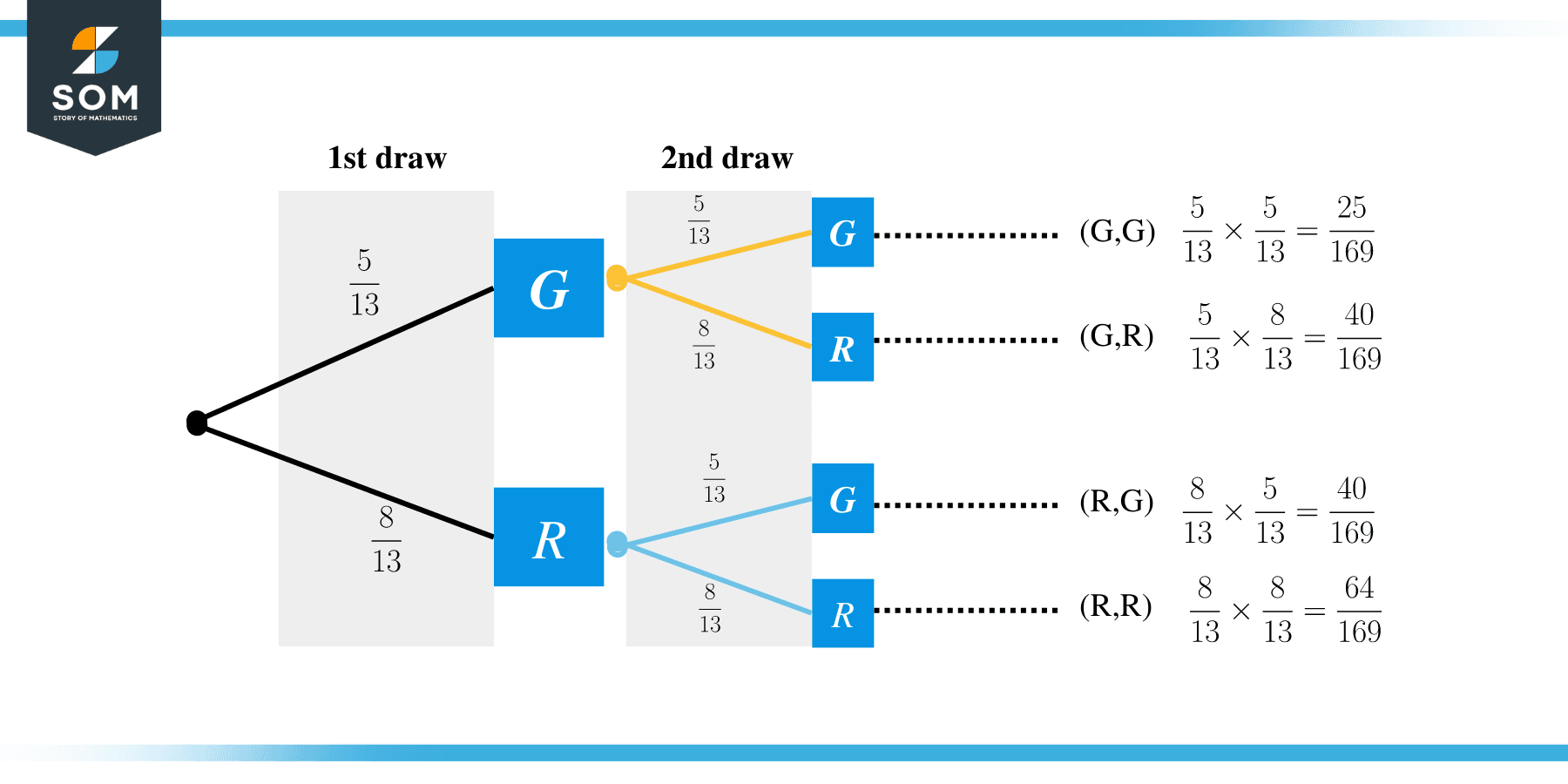
Tree Diagram for solving Probability with replacement:

We use Tree diagrams to organize information. These can be used to solve probability problems by representing all possible events and their respective outcomes. The probability of an event is written on its branch, and to calculate the overall probability, we multiply the probabilities along the branches. Let’s consider an example.

Example:

Let’s suppose there are thirteen balls in a box. Five balls are Green(G), and eight balls are Red(R). If we draw two balls, one at a time, with replacement, find the probability of the following events:

1. Both Balls are Green.
2. Both balls are Red.
3. The first ball is Green and the second is Red.
4. The first ball is Red and the second is Green.

Solution:

We can solve this question by drawing a tree diagram as shown below:

A few more examples:

Let’s consider some more examples to clarify the concept of probability with replacement further.

Example1:

Four cards are picked randomly, with replacement, from a regular deck of 52 playing cards. Find the probability that all four are aces.

Solution:

There are four aces in a deck, and as we are replacing after each sample, so

$P(\textrm{First Ace}) = P(\textrm{Second Ace}) = P(\textrm{Third Ace}) = P(\textrm{Fouth Ace}) = \frac{4}{52}$.

All four samples are independent, so

$P(\textrm{all four are aces}) = \frac{4}{52} \times \frac{4}{52} \times \frac{4}{52} \times \frac{4}{52}=\frac{1}{28561}$.

Example2:

A bag contains 3 books named Maths(M), Science(S), and Physics(P). A book is chosen at random, and after recording its name, it is returned to the bag. If this event occurred five times, find the probability of the following:

1. Each book is selected once.
2. Science is selected three times.
3. Maths is not selected.

Solution:

1. There are six possible permutations in which three books can be sampled without any book being selected twice, i.e., $\{\textrm{M}, \textrm{S}, \textrm{P}\}$, $\{\textrm{M}, \textrm{P}, \textrm{S}\}$, $\{\textrm{S}, \textrm{M}, \textrm{P}\}$, $\{\textrm{S}, \textrm{P}, \textrm{M}\}$, $\{\textrm{P}, \textrm{S}, \textrm{M}\}$, $\{\textrm{P}, \textrm{M}, \textrm{S}\}$. The probability of each permutation is the same so we show the calculation of the probability of $\{\textrm{M}, \textrm{S}, \textrm{P}\}$ only.

$P(\textrm{First book is Maths}) = \frac{1}{3}$

$P(\textrm{Second book is Science}) = \frac{1}{3}$

$P(\textrm{Third book is Physics}) = \frac{1}{3}$

Due to replacement, the probability of drawing each book is the same, and all draws are independent and so

$P(\{\textrm{M}, \textrm{S}, \textrm{P}\}) = \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3}  = \frac{1}{27}$.

Since there are six possibilities and each event is disjoint from the other, so

$P(\textrm{Each book is selected once}) = 6 \times \frac{1}{27} = \frac{2}{9}$.

2.

$P(\textrm{First book is Science}) = \frac{1}{3}$

$P(\textrm{Second book is Science}) = P(\textrm{Third book is Science}) = \frac{1}{3}$

$P(\textrm{Science is selected three times}) = \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3} = \frac{1}{29}$.

3. Let us define:

Event1: The first book is not Maths

Event2: Second book is not Maths

Event3: Third book is not Maths

$P(\textrm{Math is not selected}) = P(\textrm{Event1 and Event2 and Event3})$.  From basic probability theory,

$P(\textrm{First book is not Maths}) = 1 – P(\textrm{First book is Maths})$, so

$P(\textrm{First book is not Maths}) = 1 – \frac{1}{3} = \frac{2}{3}$.

Similarly,

$P(\textrm{Second book is not Maths}) = P(\textrm{Third book is not Maths}) = \frac{2}{3}$.

As discussed earlier, the draws in sampling by replacement are independent and so

$P(\textrm{Event1 and Event2 and Event3}) = P(\textrm{Event1}) \times P(\textrm{Event2}) \times P(\textrm{Event3})$.

$P(\textrm{Maths is not selected}) = \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} = \frac{8}{27}$.

Practice Questions

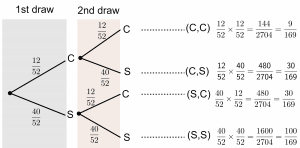
1.Two cards are picked randomly, with replacement, from a regular deck of 52 playing cards. 12 cards are court cards(C), and 40 cards are spot cards(S). Draw a tree diagram to list all possible outcomes and their corresponding probabilities.

2.The letters of the word ‘SUCCESS’ are printed on 7 cards. Jacob chooses a card at random, replaces it, then chooses a card again. Calculate the probability that only one of the cards he chooses has the letter C printed on it.

3.Two cards are picked randomly, with replacement, from a regular deck of 52 playing cards. 4 cards are Kings, and 4 cards are Queens in a deck. What is the probability that one King and one Queen are chosen?

Answer Key:

1.

2. C’ represents Not the letter C.

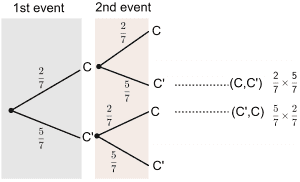
For one of the card he chooses has ‘ C ‘ printed on it: $(2/7 \times 5/7)+(5/7 \times2/7)=20/49$.

3. $P(\textrm{one King and one Queen}) = P(\textrm{1st King and 2nd Queen}) + P(\textrm{1st Queen and 2nd King})$

$\qquad \qquad \qquad \qquad \qquad \qquad \quad = \frac{4}{52}\times\frac{4}{52} + \frac{4}{52}\times\frac{4}{52}$

$\qquad \qquad \qquad \qquad  \qquad \qquad \quad = \frac{2}{169}$

Previous Lesson | Main Page | Next Lesson