Probability Without Replacement – Explanation & Examples
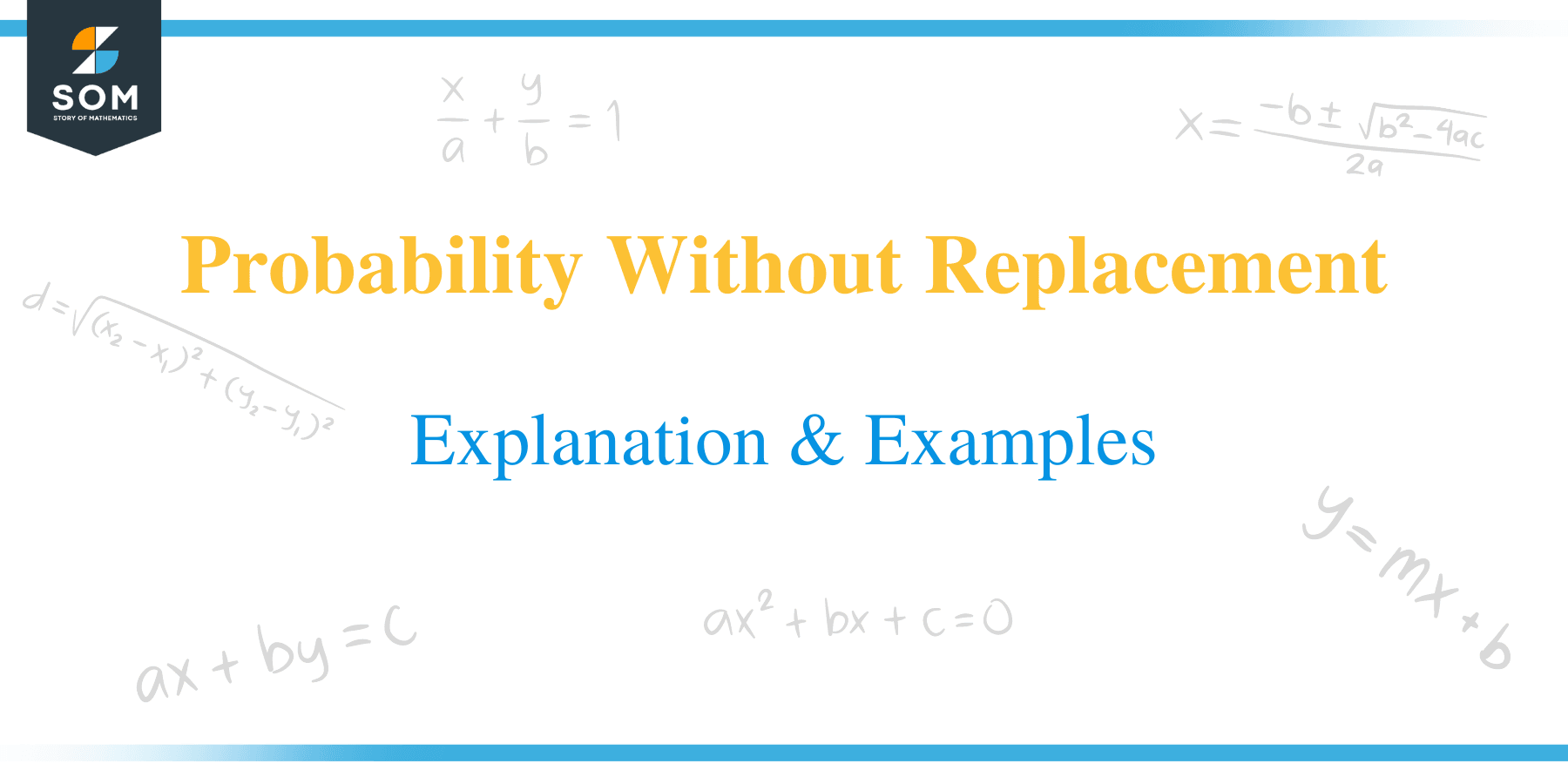Did you ever take candy from a box, gave it to your older kid (who ate the candy), then took a second candy, and gave it to your younger kid? If your answer is yes, you have already come across a nice story involving dependent probability, generally termed as Probability Without Replacement. But if your older kid had returned the candy and you had put it back in the box, the second event would have been independent. The box of sweets (sample space) would have remained the same for the second event — probability with replacement.
Probability without replacement involves dependent events where the preceding event has an effect on the probability of the next event.
Probability Without Replacement may initially sound tricky but trust me; it is one of the most specific mathematics topics. This lesson will clear your concept about dependent probability, and we will learn step by step how to calculate probability without replacement. This lesson will also help you understand how to use a probability tree diagram involving dependent probability — probability without replacement.
What does probability without replacement mean?
Probability without replacement means once we draw an item, then we do not replace it back to the sample space before drawing a second item. In other words, an item cannot be drawn more than once.
For example, if we draw a candy from a box of 9 candies, and then we draw a second candy without replacing the first candy. Of course, the sample space would no longer remain 9 for the second event because we have not replaced the first candy. Thus, the sample space would be 8 for the second event. In other words, the sample space has been changed for the second event.
We use probability without replacement to solve the problems where the sample space changes for different events and the occurrence of the next event depends upon what happens in the preceding event.
How to calculate probability without replacement?
Now that we briefly understand dependent probability – before diving deep into calculating probability without replacement – let’s first try to visualize what dependent events are and how the preceding event can affect the next event.
For example, a box contains $4$ blue candies and $5$ orange candies, as shown below.
Let us consider that event A is getting a blue candy. As there are $4$ blue candies, so the number of ways it can happen = $4$. Also, the total number of candies is $9$, so the total number of outcomes = $9$.
Let’s suppose $P(A)$ represents the probability of getting a blue candy. Thus, we can calculate the probability of getting a blue candy such as:
P(A) = number of ways it can happen $\displaystyle /$ total number of outcomes
$P(A) = \frac{4}{9}$
Thus, the probability of getting a blue candy is $4$ in $9$, as shown below.
Now going ahead, we need to understand that the probabilities change if we take any candy out.
Here, let us check the two scenarios such as:
Scenario 1:
If we draw a orange candy before, then the probability of a blue candy next is $4$ in $8$, as shown below.
Scenario 2:
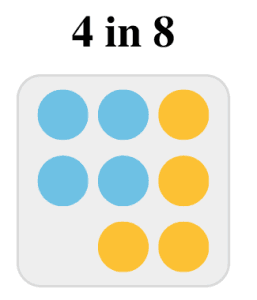
And if we draw a blue candy before, then the probability of a blue candy next is $3$ in $8$, as shown below.
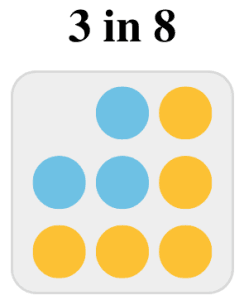
Here is the complete snapshot of what we learned.
The probabilities change because we are removing candies from the box. The next event tends to depend on what occurs in the preceding event, also known as a dependent.
Thus, when we remove the candies each time without replacement, then the probabilities change, and the events are dependent.
A tree diagram is a pleasing way to visualize the concept involving probability without replacement.
Taking the same example, there is a $\frac{5}{9}$ chance of drawing a orange candy from the box, and a $\frac{4}{9}$ chance for blue candy such as:
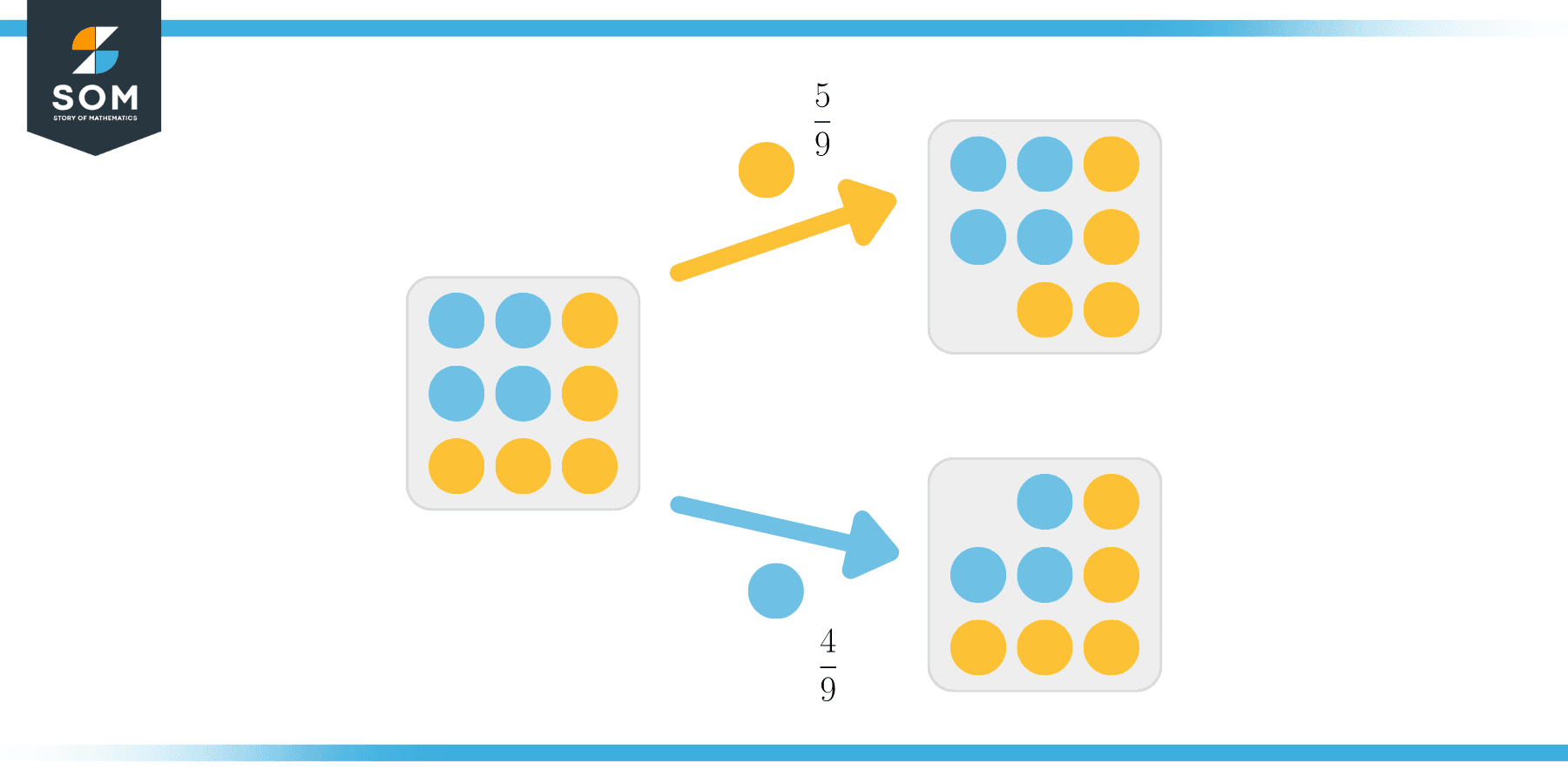
Going ahead, let’s check what occurs when we draw a second candy.
If a blue candy is chosen first, there is a $\frac{4}{8}$ probability of getting a blue candy and a $\frac{4}{8}$ probability of getting a blue candy. The reason is that after $1$ orange candy is taken, we have $8$ candies left, of which $4$ are orange, and $4$ are blue.
If a blue candy is chosen first, there is a $\frac{5}{8}$ probability of getting a orange candy and a $\frac{3}{8}$ probability of getting a blue candy. Again, after $1$ blue candy is taken, we have $8$ candies left, of which $3$ are orange, and $5$ are blue.
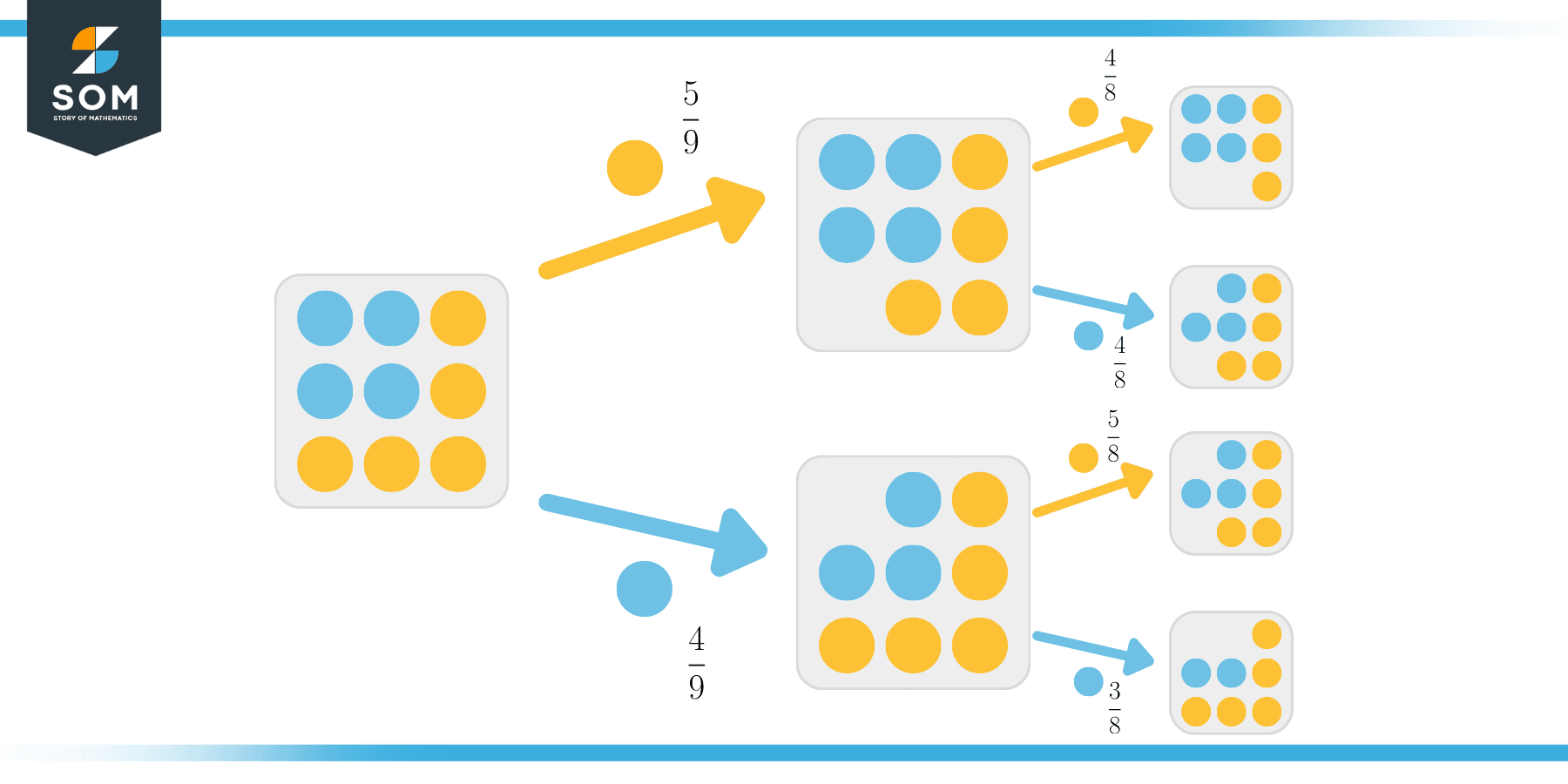
Now, we can determine a variety of probabilities without replacement with the help of the above tree diagram.
For example, let’s say we need to determine the probability of drawing $2$ blue candies. We can visualize from the tree diagram that it is a $\frac{4}{9}$ probability followed by a $\frac{3}{8}$ probability, as shown in the tree diagram below.
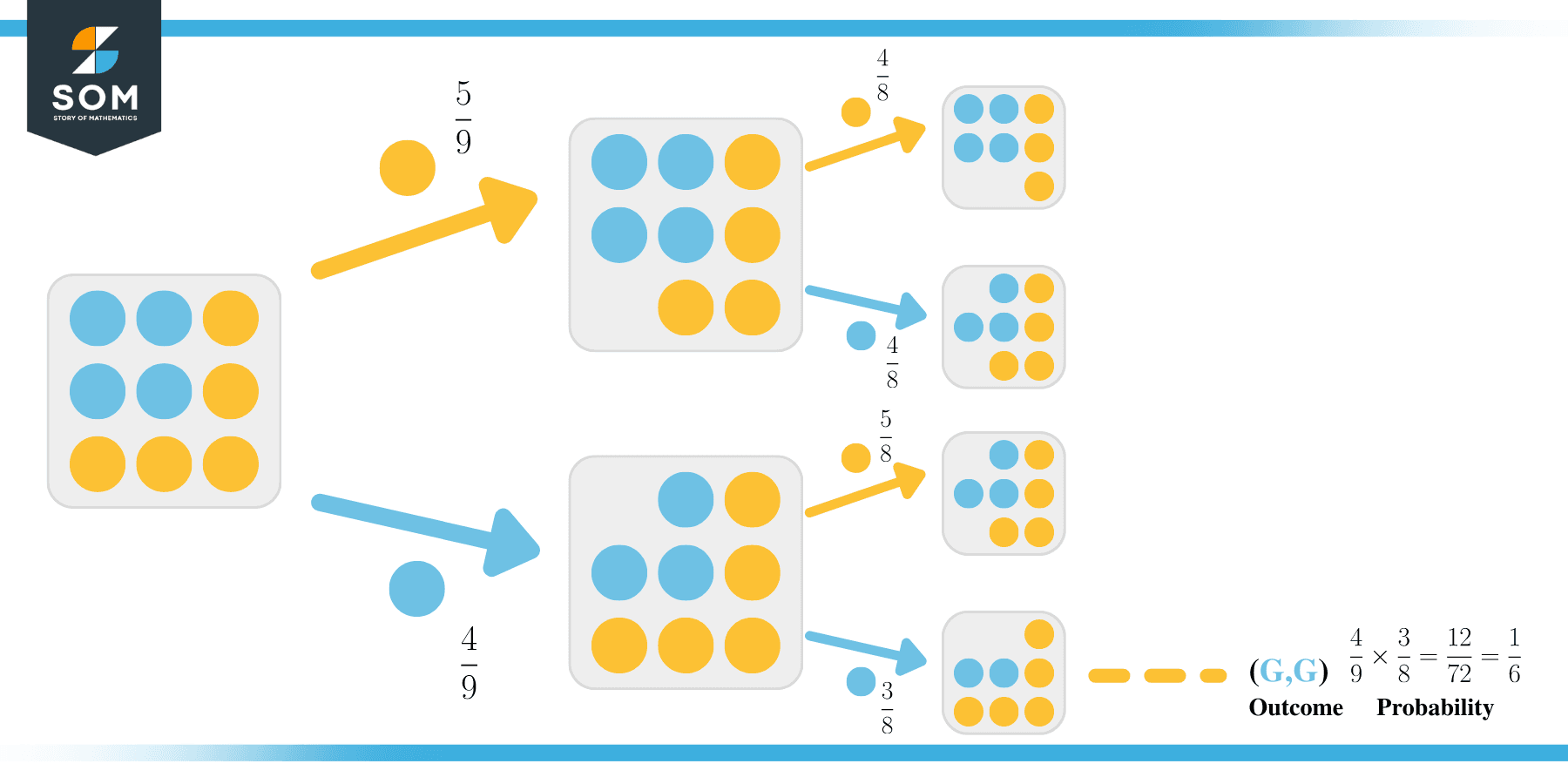
From the tree diagram, we can easily figure out that we have just multiplied the probabilities such as:
$\frac{4}{9}\times \frac{3}{8}=\frac{12}{72}=\frac{1}{6}$
Thus, the probability of drawing 2 blue candies is $\frac{1}{6}$.
Probability without replacement formula
In our example, event $A$ is getting a blue candy, and $P(A)$ represents the probability of getting a blue candy with a probability of $\frac{4}{9}$:
$P(A) = \frac{4}{9}$
Also, event $B$ is getting a blue candy second, but for that, we have two scenarios such as:
- If we chose a blue candy first, the probability is now $\frac{3}{8}$.
- If we chose a orange candy first, the probability is now $\frac{4}{8}$.
It is up to us which one we chose. And we can use the notation $P(B\mid A)$ read as ‘the probability of $B$ given $A$‘. Please note that the symbol ‘$|