Product rule – Derivation, Explanation, and Example

The product rule will save you a lot of time finding the derivative of factored expressions without expanding them. This rule’s other name is the Leibniz rule – yes, named after Gottfried Leibniz. The product rule is such a game-changer since this allows us to find the derivatives of more complex functions.

The product rule allows us to find the derivative of two functions’ product using the respective functions’ corresponding derivatives.

This article will show how we can easily find the derivative of $f(x) \cdot g(x)$ and learn when this rule is most helpful. To master the product rule’s formula, we will derive the formula and try out a wide range of examples to show you how we can apply this product rule easily.

Finding the derivative of complex functions will also require other fundamental derivative rules, so make sure to refresh your notes on the previous rules you’ve already learned. For now, let’s dive right into understanding how the product rule works.

What is the product rule?                

The product rule is an essential derivative rule used to find the derivative of a function that can be expressed as a product of two simpler expressions. A great example of this type of function is $h(x) = (x^3 – 2x + 1)(x^3 – 4x^2 + 1)$.

Without the product rule, our option is to either use the formal definition of derivatives or expand the function to apply sum, difference, and power rules. But either way, it will be extremely tedious and will take a lot of our time. This is where the product rule enters.

According to the product rule, when we have $f(x)\cdot g(x)$, the derivative of this expression is simply the sum of the products of $\boldsymbol{f(x)}$ and $\boldsymbol{g’(x)}$ plus the product of $\boldsymbol{g(x)}$and $\boldsymbol{f’(x)}$.

\begin{aligned} \dfrac{d}{dx} [f(x)\cdot g(x)] &= f(x) \dfrac{d}{dx} [g(x)]+ g(x) \dfrac{d}{dx} [f(x)]\\&= f*(x)g'(x) + g(x)f'(x)\end{aligned}

Through the product rule, we’ll only be needing the derivative of each factored expression and the original expressions that will be multiplied. Will this make the process easier? Definitely.

• For some, since $f’(x)$ and $g’(x)$ will have lower degrees, the products $f’(x)g(x)$ and $g’(x)f(x)$ will be much simpler.

• There are also times that the derivative of the factored expression will significantly simplify the process.

Deriving the product rule formula

Now that we’ve understood how this rule works let’s appreciate it even more by understanding how this product rule was derived using limit laws and the derivative’s formal definition.

If we have $f(x) \cdot g(x)$, we can find $\dfrac{d}{dx} [f(x)\cdot g(x)]$ using the formal definition of derivatives.

\begin{aligned} \dfrac{d}{dx} [f(x)\cdot g(x)] &= \lim_{h \rightarrow} \dfrac{[f(x +h)\cdot g(x+h)] – [f(x)\cdot g(x)]}{h}\end{aligned}

We can rewrite this expression using different algebraic manipulation techniques, as shown below.

\begin{aligned} \dfrac{d}{dx} [f(x)\cdot g(x)] &= \lim_{h \rightarrow 0} \dfrac{f(x+h)g(x +h)-f(x)g(x + h) + f(x)g(x + h) – f(x)g(x)}{h}\\&=\lim_{h \rightarrow 0} \left\{\left[\dfrac{f(x + h) -f(x)}{h} \right ]g(x + h) – f(x )\left[\dfrac{g(x + h) -g(x)}{h} \right ]\right\}\end{aligned}

We can use the limit laws and factor out $f(x)$ and $g(x)$ whenever possible.

\begin{aligned} \dfrac{d}{dx} [f(x)\cdot g(x)] &= \left[\lim_{h \rightarrow 0}\dfrac{f(x + h) -f(x)}{h} \right ] \lim_{h \rightarrow 0} g(x + h) + f(x )\left[\lim_{h \rightarrow 0}\dfrac{g(x + h) -g(x)}{h} \right ]\\&= \dfrac{d}{dx} [f(x)] \cdot g(x + 0) + [\dfrac{d}{dx} g(x)] \cdot f(x)\\&= f'(x)g(x) + g'(x)f(x)\end{aligned}

Here’s a visualization of how the product rule can be derived as well:

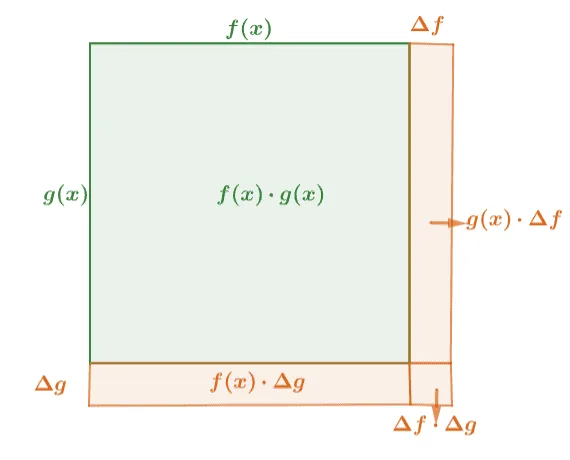
Hence, we’ve established the fact that $\dfrac{d}{dx} [f(x)g(x)] = f(x)g’(x) + g(x)f’(x)$.

How to use the product rule?

Let’s go ahead and understand how we can apply the product rule to find the derivative of a function that benefits from this rule. Here are some tips that can help you in applying this rule easily:

• Take note of the derivative of the two expressions.

• Alternate the pairings when you start multiplying: pair the first factor with the derivative of the second and do the same for the second factor with the first factor’s derivative.

• Add the two resulting expressions to find the derivative of the original function.

Once we have the expressions for $f(x)$, $g(x)$, $f’(x)$ and $g’(x)$, let us share a quick trick to help you master this topic:

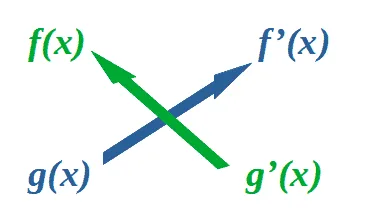
We can write the expressions this way so we can cross-multiply them and come up with the derivative of $f(x)g(x)$:

\begin{aligned}\dfrac{d}{dx} [f(x) \cdot g(x)] = {\color{green}f(x) g’(x) } + {\color{blue} g(x)f’(x)} \end{aligned}

Let’s say we want to find the derivative of $x^2 \sin x$. We can use the product rule as well as the following rules to find $\dfrac{d}{dx} (x^2 \sin x)$:

• Derivative of sine: $\dfrac{d}{dx} \sin x =\cos x$

• Power rule: $\dfrac{d}{dx} x^n = nx^{n-1}$

We can express $x^2 \sin x$ as a product of $x^2$ and $\sin x$, so this shows that we can use the product rule as shown below:

This shows that through the product rule, we can immediately find the derivative of $x^2 \sin x$. In fact, we have $\dfrac{d}{dx} (x^2\sin x) = x^2\cos x + 2x \sin x$.

Check out the sample problems below for you to work on and help you master this technique.

Example 1

Find the derivative of $h(x) = 3x^5 \tan x$ using the product rule.

Solution

We can write $h(x)$ as a product of two expressions: $(3x^5)$ and $\tan x$. This shows that we can use the product rule to differentiate $h(x)$. Let’s recall the following derivative rules (aside from the product rule) that we’ll be using to find $h’(x)$:

• The constant multiple rule: $\dfrac{d}{dx} cf(x) = c\dfrac{d}{dx} f(x)$.

• The power rule: $\dfrac{d}{dx} x^n = nx^{n -1}$.

• The derivative of tangent: $\dfrac{d}{dx} \tan x = \sec^2 x$.

This example shows you that thanks to the product rule, we can easily differentiate $h(x) = 3x^5 \tan x$. We have $h’(x) = 3x^5\sec^2 x + 15x^4 \tan x$ or $h’(x) = 3x^4(x \sec^2 x + 5\tan x)$.

Example 2

Find the derivative of $y = e^x(x^6 – 5x^4 + 2x) $ using the product rule. (Here’s a tip: $\dfrac{d}{dx} e^x = e^x$)

Solution

We can see two factors here: $e^x$ and $x^6 – 5x^4 + 2x$. The tip already makes our lives easier since $\dfrac{d}{dx} e^x$ will remain $e^x$. For the second factor, we can use the following rules:

• The sum rule for derivatives: $\dfrac{d}{dx} [f(x) + g(x)] = f’(x) + g(x)$.

• Constant multiple rule: $\dfrac{d}{dx} cf(x) = c\dfrac{d}{dx} f(x)$.

• Power rule: $\dfrac{d}{dx} x^n = nx^{n -1}$

Let’s go ahead and apply the product rule to find the derivative of $y=e^x(x^6 – 5x^4 + 2x) $.

This means that through product rule (and other fundamental derivative rules, of course), we were able to differentiate $y = e^x(x^6 – 5x^4 + 2x) $. Hence, we have $y’ =e^x(x^6 -5x^4 – 20x^3 + 2x +2)$.

Practice Questions

1. Find the derivative of $h(x) = -6x^4 \cos x$ using the product rule.

2. Find the derivative of $h(x) = 12x^8 \tan x$ using the product rule.

3.Find the derivative of $y = e^x \sin x$ using the product rule.

4.Find the derivative of $y = e^x (-12x^5 – 6x^2 + 7)$ using the product rule.

4.Find the derivative of $y = \sqrt{x}(x^4 – 1)$ using the product rule.

Answer Key

1. $h’(x) = -24x^3\cos x +6x^4 \sin x = 6x^3(-4\cos x + x\sin x)$

2. $h’(x) = 12x^8 \sec^2 x + 96x^7 \tan x = 12x^7(x\sec^2 x + 8\tan x)$

3. $y’ = e^x (\sin x + \cos x)$

4. $y’ = e^x (7 – 12 x – 6 x^2 – 60 x^4 – 12 x^5)$

5. $y’ = \dfrac{9}{2} x^{\frac{7}{2}} – \dfrac{1}{2\sqrt{x}} = \dfrac{9x^4 -1}{2\sqrt{x}}$

Images/mathematical drawings are created with GeoGebra.