Pythagorean Triples – Explanation & Examples

What is a Pythagorean triple?

Pythagorean triple (PT) can be defined as a set of three positive whole numbers that perfectly satisfy the Pythagorean theorem: a² + b² = c².

This set of numbers are usually the three side lengths of a right triangle. Pythagorean triples are represented as: (a, b, c), where, a = one leg; b = another leg; and c = hypotenuse.

There are two types of Pythagorean triples:

• Primitive Pythagorean triples
• Non-primitive Pythagorean triples

Primitive Pythagorean triples

A primitive Pythagorean triple is a reduced set of the positive values of a, b, and c with a common factor other than 1. This type of triple is always composed of one even number and two odd numbers.

For example, (3, 4, 5) and (5, 12, 13) are examples of primitive Pythagorean triples because each set has a common factor of 1 and also satisfies the

Pythagorean theorem: a² + b² = c².

• (3, 4, 5) → GCF =1

a² + b² = c²

3² + 4² = 5²

9 + 16 = 25

25 = 25

• (5, 12, 13) → GCF = 1

a² + b² = c²

5² + 12² = 13²

25 + 144 = 169

169 = 169

Non-primitive Pythagorean triples

A non-primitive Pythagorean triple, also known as the imperative Pythagorean triple, is a set of positive values of a, b, and c with a common factor greater than 1. In other words, the three sets of positive values in a non-primitive Pythagorean triple are all even numbers.

Examples of non-primitive Pythagorean triples include: (6,8,10), (32,60,68), (16, 30, 34) etc.

• (6,8,10) → GCF of 6, 8 and 10 = 2.

a² + b² = c²

6² + 8² = 10²

36 + 64 = 100

• = 100
• (32,60,68) → GCF of 32, 60 and 68 = 4

a² + b² = c²

32² + 60² = 68²

1,024 + 3,600 = 4,624

4,624 = 4,624

Other examples of commonly used Pythagorean triples include: (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25) , (20, 21, 29) , (12, 35, 37), (9, 40, 41), (28, 45, 53), (11, 60, 61), (16, 63, 65), (33, 56, 65), (48, 55, 73), etc.

Properties of Pythagorean triples

From the above illustration of different types of Pythagorean triples, we make the following conclusions about Pythagorean triples:

• A Pythagorean triple cannot have composed of only odd numbers.
• Similarly, a triple a Pythagorean triple can never contain one odd number and two odd numbers.
• If (a, b, c) is a Pythagorean triple, then either a or b is the short or long leg of the triangle, and c is the hypotenuse.

Pythagorean Triples Formula

The Pythagorean triples formula can generate both primitive Pythagorean triples and non-primitive Pythagorean triples.

Pythagorean triples formula is given as:

(a, b, c) = [ (m² − n²); (2mn); (m² + n²)]

Where m and n are two positive integers and m > n

NOTE: If one member of the triple is known, we can obtain the remaining members by using the formula: (a, b, c) = [ (m²-1), (2m), (m²+1)].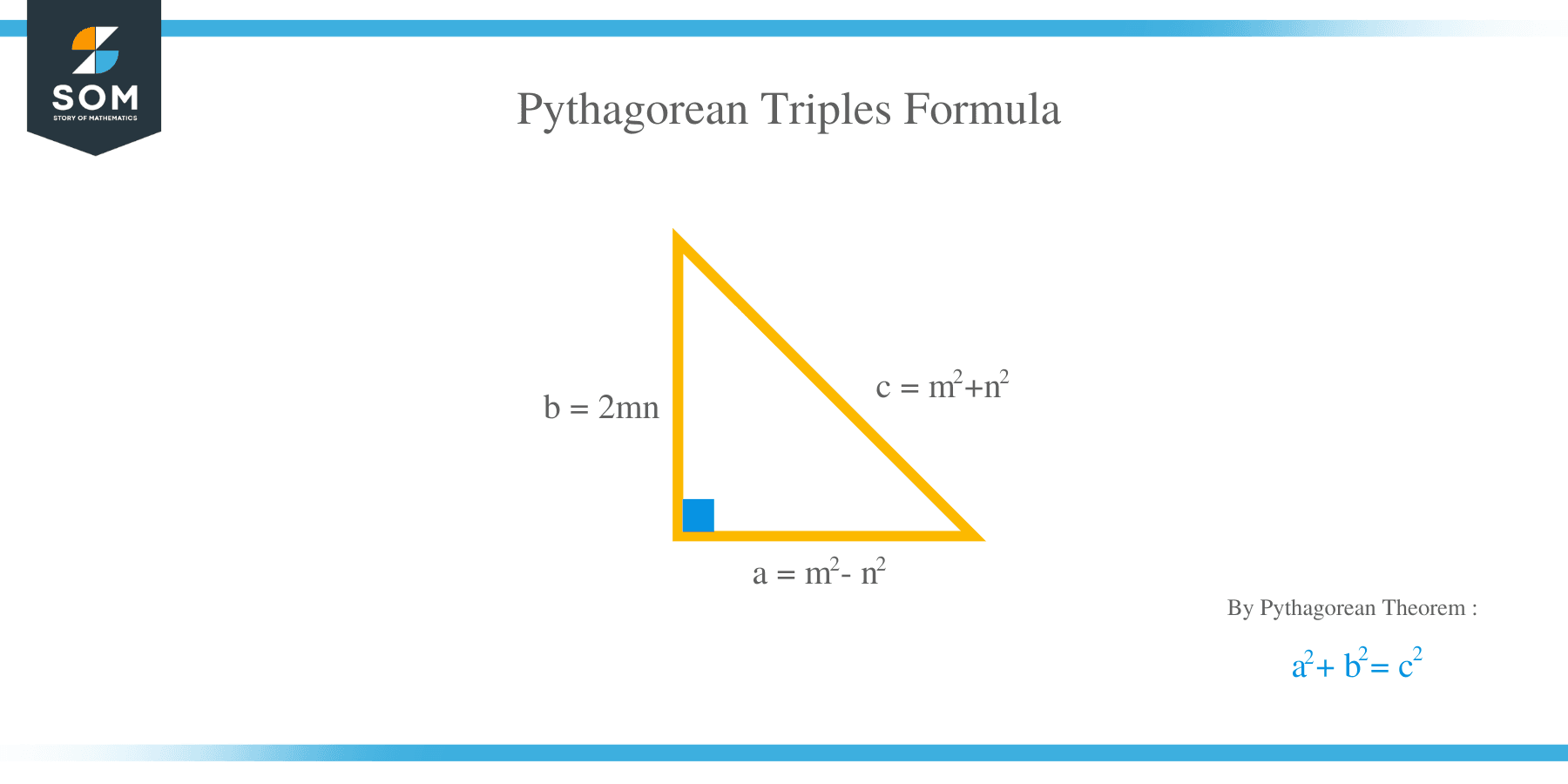

Example 1

What is the Pythagorean triple of two positive numbers, 1 and 2?

Solution

Given the Pythagorean triples formula: (a, b, c) = (m² − n²; 2mn; m² + n²), where; m > n.

So, let m = 2 and n = 1.

Substitute the values of m and n into the formula.

⇒ a = 2² − 1² = 4 − 1 = 3

a =3

⇒ b = 2 × 2 × 1 = 4

b = 4

⇒ c = 2² + 1² = 4 + 1 = 5

c = 5

Apply the Pythagorean theorem to verify that (3,4,5) is indeed a Pythagorean triple

⇒ a² + b² = c²

⇒ 3² + 4² = 5²

⇒ 9 + 16 = 25

⇒ 25 = 25.

Yes, it worked! Therefore, (3,4,5) is a Pythagorean triple.

Example 2

Generate a Pythagorean triple from two integers 5 and 3.

Solution

Since m must be greater than n (m > n), let m= 5 and n = 2.

a = m² − n²

⇒a= (5)² −(3)² = 25−9

= 16

⇒ b = 2mn = 2 x 5 x 3

= 30

⇒ c = m² + n² = 3² + 5²
= 9 + 25
= 34

Hence, (a, b, c) = (16, 30, 34).

Verify the answer.

⇒ a² + b² = c²

⇒ 16² + 30² = 34²

⇒ 256 + 900 = 1,156

1,156 = 1,156 (True)

Therefore, (16, 30, 34) is indeed a Pythagorean triple.

Example 3

Check if (17, 59, 65) is a Pythagorean triple.

Solution

Let, a = 17, b = 59, c = 65.

Test if, a² + b² = c².

a² + b² ⇒ 17² + 59²

⇒ 289 + 3481 = 3770

c² = 65²

= 4225

Since 3770 ≠ 4225, then (17, 59, 65) is not a Pythagorean triple.

Example 4

Find the possible value of ‘a’ in the following Pythagorean triple:(a, 35, 37).

Solution

Apply the Pythagorean equation a² + b² = c².

a² + 35² = 37².

a² = 37²−35²=144. ​

√a² = √144

a = 12.

Example 5

Find the Pythagorean triple of a right triangle whose hypotenuse is 17 cm.

Solution

(a, b, c) = [ (m²-1), (2m), (m²+1)]

c = 17 = m²+1

17 – 1 = m²

m² = 16

m = 4.

Therefore,

b = 2m = 2 x 4

= 8

a = m² – 1

= 4² – 1

= 15

Example 6

The smallest side of a right triangle is 20mm. Find the Pythagorean triple of the triangle.

Solution

(a, b, c) =[(2m), (m²-1), (m²+1)]

20 =a = 2m

2m = 20

m =10

Substitute m = 10 into the equation.

b = m² – 1

= 10² – 1= 100 – 1

b = 99

c = m²+1

= 10² + 1

= 100 + 1 = 101

PT = (20, 99, 101)

Example 7

Generate a Pythagorean triple from two integers 3 and 10.

Solution

(a, b, c) = (m² − n²; 2mn; m² + n²).

a = m² − n²

= 10² – 3² = 100 – 9

= 91.

b = 2mn = 2 x 10 x 3

= 60

c = m² + n²

= 10² + 3² = 100 + 9

= 109.

PT = (91, 60,109)

Verify the answer.

a² + b² = c².

91² + 60² = 109².

8,281+ 3,600=11,881

11,881=11,881 (True)

Example 8

Check whether the set (24, 7, 25) is a Pythagorean triple.

Solution

Let a = 24, b = 7 and c = 25.

By Pythagorean theorem: a² + b² = c²

7² + 24² = 625

49 + 576 = 625 (True)

Therefore, (24, 7, 25) is a Pythagorean triple.

Example 9

Find the Pythagorean triplet of a right triangle whose one side is 18 yards.

Solution

Given the formula: (a, b, c) = [ (m²-1), (2m), (m²+1)].

Let a or b = 18 yards.

2m = 18

m = 9.

Substitute m = 9 into the formula.

c = m² + 1

= 9² + 1 = 81

b or a = m² -1 = 9² -1

= 80

Therefore, the possible triplets are; (80, 18, 81) or (18, 80, 81).