- Home
- >
- Quadric surfaces – Definition, Types, and Examples
JUMP TO TOPIC
Quadric Surfaces – Definition, Types, and Examples
Knowing about common quadric surfaces will help us understand how second-degree equations can be graphed in space. Ellipsoids and hyperboloids are just two of the many quadric surfaces that are widely used in early computer-aided architecture and engineering models. Of course, learning about quadric surfaces will also help us extend our knowledge of vectors and multivariable calculus.
Quadric surfaces are graphs formed from second-degree equations containing three variables and positioned in the three-dimensional coordinate system. They are the 3D counterparts of conic sections and have six distinct types.
In this article, we’ll show you how quadric surfaces will extend our knowledge of conic sections to a 3D coordinate system. This is why it’ll be extremely helpful if you still remember your fundamentals on conics but if not, open this link on a new tab in case you need a quick refresher.
Our discussion will cover all the fundamentals needed to master this topic. This means that our goal is for you to:
- Understand the different types of quadric surfaces
- Learn the unique properties and general forms of these quadric surfaces
- Know how to visualize and graph them in a three-dimensional coordinate system
What Are Quadric Surfaces?
Quadric surfaces are surfaces that are defined by different types of second-order equations with three variables: $x$, $y$, and $z$. These surfaces are defined by the general form shown below.
\begin{aligned}Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Jz + K &= 0\end{aligned}
This general form will return different types of quadric surfaces that we can graph in a three-dimensional coordinate system. In fact, through rotation and translation, we can simplify the general form into two standard forms as shown below:
\begin{aligned}Ax^2 + By^2 + Cz^2 + J &= 0\\ Ax^2 + By^2 +Iz &= 0\end{aligned}
As we have mentioned, quadric surfaces are closely related to conic sections. That’s because the cross-sections or traces of these quadric surfaces are conic sections.
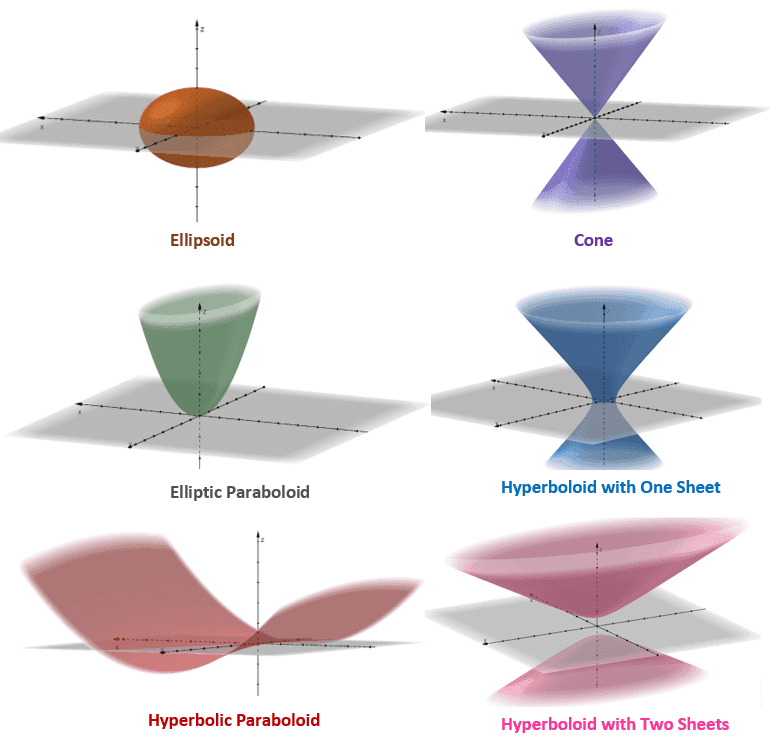
The six distinct quadric surfaces that we will be discussing are ellipsoid, elliptic paraboloid, hyperbolic paraboloid, cone, and hyperboloids (in one sheet and two sheets). Just by seeing the six graphs shown above, we can see that the quadric surfaces are indeed the 3D counterparts of conic sections.
In the next sections, we’ll cover the important properties of these six quadric surfaces, and we’ll eventually learn how to model second-degree equations in terms of $x$, $y$, and $z$.
How To Identify Quadric Surfaces?
We can identify quadric surfaces easily by knowing the general forms, properties, and unique characteristics of each of the quadric surfaces. In this section, we’ll learn what makes each of the quadric surfaces unique and eventually learn how to easily identify them using their equations, graphs, and cross-sections.
Ellipsoid: $\boldsymbol{\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2} = 1}$
In a two-dimensional coordinate system, we’ve learned how to identify and graph ellipses. This time, we’ll study its counterpart in a three-dimensional coordinate system: the ellipsoid. As with circles and ellipses, the sphere is a special type of ellipsoid, where $\boldsymbol{a = b= c= 1}$.
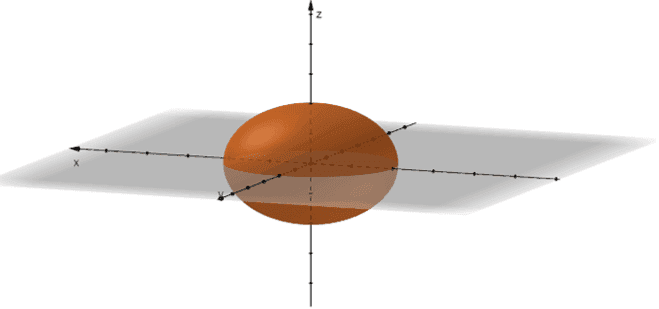
The ellipsoid contains ellipses as their traces (or cross-sections), as shown below. Ellipsoids are symmetric with respect to the coordinate planes.
- The ellipse, $\dfrac{x^2}{y^2} = 1$, is the cross-section formed when we set $z=0$.
- The ellipse, $\dfrac{y^2}{z^2} = 1$, is the cross-section formed when we set $x=0$.
- The ellipse, $\dfrac{x^2}{z^2} = 1$, is the cross-section formed when we set $y=0$.
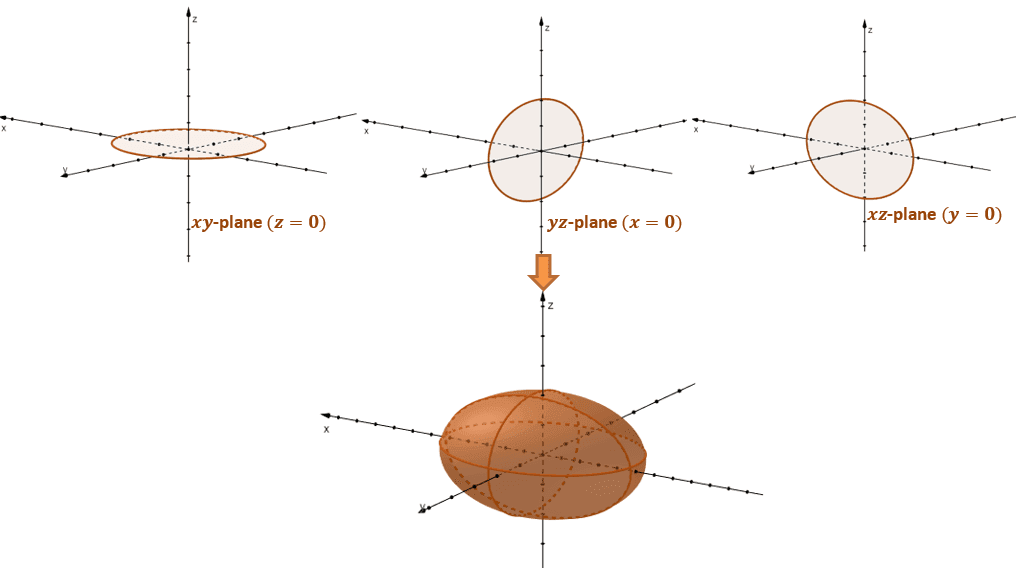
This makes sense since each set of traces are symmetric with respect to their corresponding planes. This also makes ellipsoids one of the easiest quadric surfaces to graph!
Here are some important properties of ellipsoids that can help you in identifying and graphing them:
Intercepts | $(0,0, \pm a)$, $(0,0, \pm b)$, $(0,0, \pm c)$ |
Sections | Ellipses |
Symmetry | All coordinate planes |
Center | The origin unless equation is shifted with respect to $x$, $y$, or $z$. |
Elliptic Paraboloid: $\boldsymbol{\dfrac{z}{c} = \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}}$
The easiest way to determine whether the quadric surface is an elliptic paraboloid is through its general form. Only $\boldsymbol{x}$ and $\boldsymbol{y}$ are in the second degree and the two terms are added.
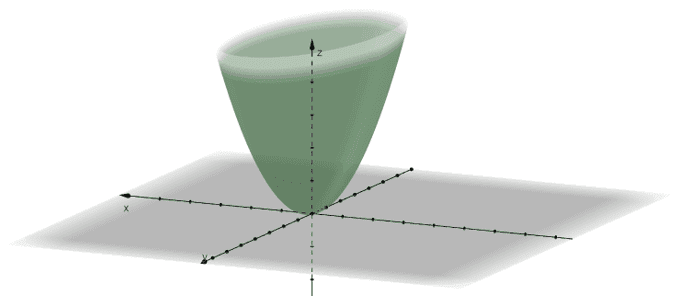
This elliptic paraboloid has the $z$-axis as its axis of symmetry. Here are the general forms for the hyperboloid:
- Axis of symmetry at the $x$-axis: $\dfrac{x}{a} = \dfrac{y^2}{b^2} + \dfrac{z^2}{c^2}$.
- Axis of symmetry at the $y$-axis: $\dfrac{y}{b} = \dfrac{x^2}{a^2} + \dfrac{z^2}{c^2}$.
The elliptic paraboloid parabola as traces and these planes are parallel to the $xz$ and $yz$-planes. The section parallel to the $xy$-plane will have ellipses as its traces. Hence, the name of this quadric surface: elliptical paraboloid.
The image above shows the breakdown the traces of an elliptic paraboloid. As expected, we have the vertical traces are parabolas while the horizontal traces are ellipses. Here are other important characteristics of elliptic paraboloids:
Intercepts | $(0,0, 0)$ |
Sections | Vertical traces: Parabola $z = \dfrac{x^2}{a^2}$, when $y =0$ $z = \dfrac{y^2}{b^2}$, when $x =0$ Horizontal traces: Ellipse $ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 0$ |
Symmetry | About the $xz$ and $yz$ planes. |
Center | The origin unless equation is shifted with respect to $x$, $y$, or $z$. |
Hyperbolic Paraboloid: $\boldsymbol{\dfrac{z}{c} = \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2}}$
The right-hand side of the hyperbolic paraboloid’s general form is similar to the hyperbola’s equation. We have $\boldsymbol{x}$ and $\boldsymbol{y}$ in the second degree and the operation between them is subtraction. We then equate the expression to $\dfrac{z}{c}$.
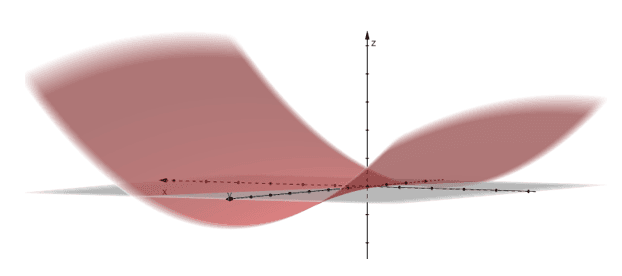
The graph shows why the hyperbolic paraboloid is known to have a saddle-shaped figure. Similar to parabolic hyperboloids, we can see that the hyperbolic paraboloid contains parabolas as vertical traces and hyperbolas as horizontal traces.
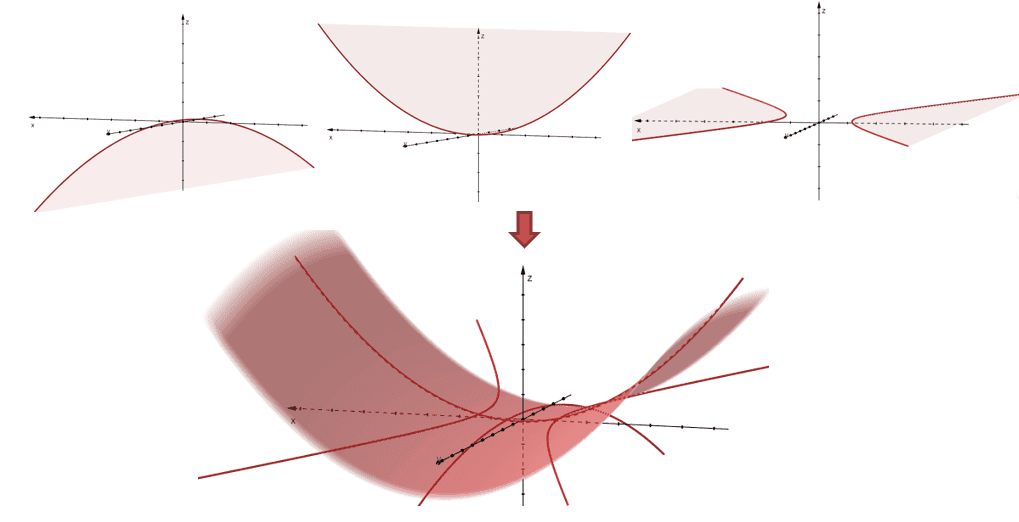
These are some interesting properties that we can observe from the hyperbolic paraboloid:
Intercepts | $(0,0, 0)$ |
Sections | Vertical traces: Parabola $z = \dfrac{x^2}{a^2}$, when $y =0$ $z = -\dfrac{y^2}{b^2}$, when $x =0$ Horizontal traces: Hyperbola $ \dfrac{x^2}{a^2} – \dfrac{y^2}{b^2} = 0$, when $z =0$ |
Symmetry | About the $xz$ and $yz$ planes. |
Center | The origin unless equation is shifted with respect to $x$, $y$, or $z$. We call this the saddle point. |
Cone: $\boldsymbol{\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2} –\dfrac{z^2}{c^2}=0}$
The cone’s general form is similar to the ellipsoid but this time, $\dfrac{z^2}{c^2}$ is negative, and the right-hand side is equal to zero.
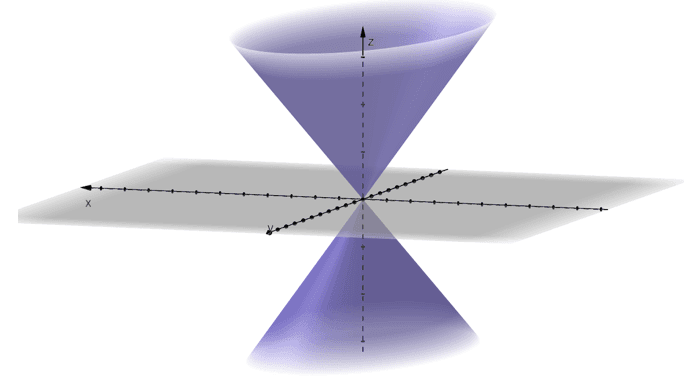
From the name of this quadric surface, we’re expecting the bases of the cone to be ellipses. The remaining section will contain traces that are planes (more often, are hyperbolas too).
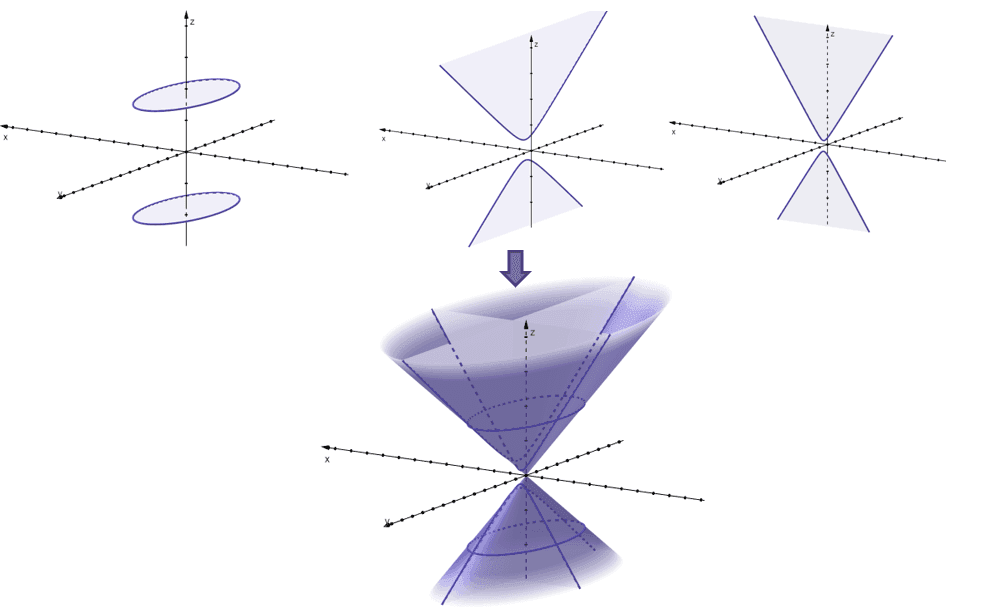
Here’s a summary of some interesting characteristics you can observe from the quadric surface – cone.
Intercepts | $(0,0, 0)$ |
Sections | Vertical traces: Parabola $z = \pm \dfrac{x}{a}$, when $y =0$ $z = \pm \dfrac{y}{b}$, when $x =0$ Horizontal traces: Hyperbola $ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 0$, when $z=0$ |
Symmetry | About the $xz$ and $yz$ planes. |
Center | The origin unless equation is shifted with respect to $x$, $y$, or $z$. |
Hyperboloid With One Sheet: $\boldsymbol{\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2} –\dfrac{z^2}{c^2}= 1}$
The equation of a hyperboloid with one sheet is similar to that of the cone except that the right-hand side of the equation is equal to $\boldsymbol{1}$. The quadric surface’s graph looks like a cone but with a widened center.
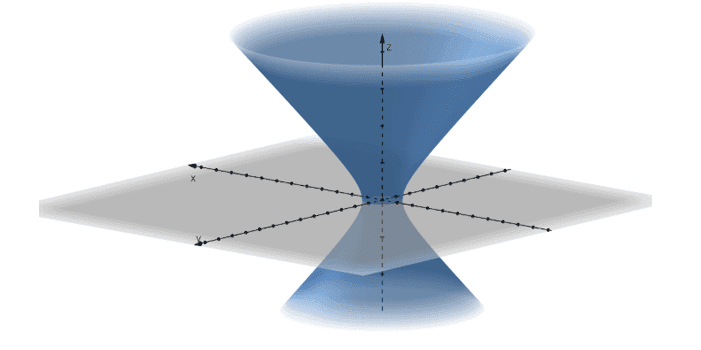
This hyperboloid has the $z$-axis as its axis of symmetry. Here are the general forms for the hyperboloid:
- Axis of symmetry at the $x$-axis: $\dfrac{x^2}{a^2}+ \dfrac{z^2}{c^2} –\dfrac{y^2}{b^2}= 1$.
- Axis of symmetry at the $y$-axis: $\dfrac{z^2}{c^2}+ \dfrac{y^2}{b^2} –\dfrac{x^2}{a^2}= 1$.
The horizontal traces of this quadric surface are ellipses, while the vertical traces are hyperbolas. Below are examples of traces from the $xz$, $yz$, and the $xy$-planes.
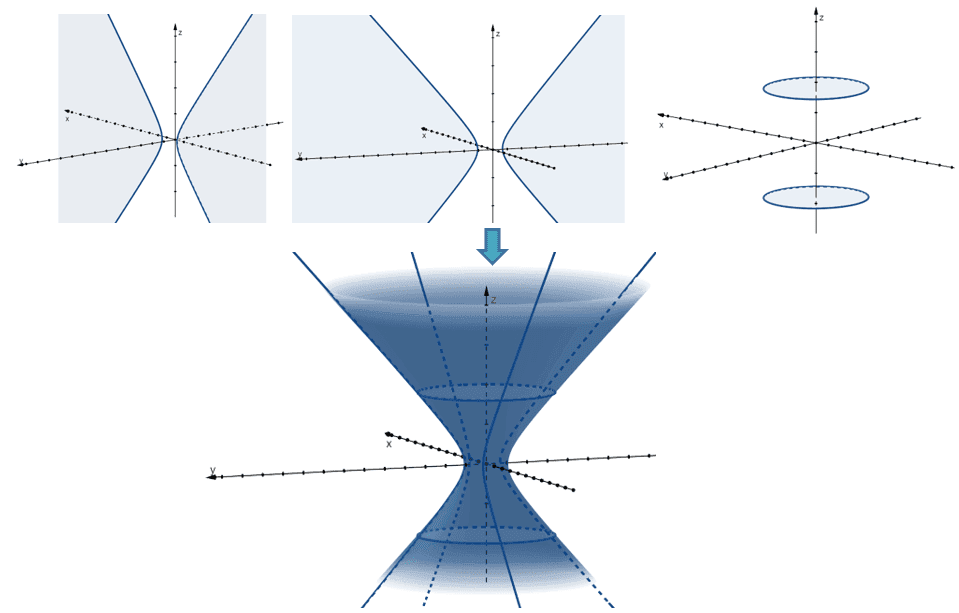
This table summarizes the key properties of hyperboloids with one sheet.
Intercepts | $(\pm a,0, 0)$, $(0, \pm b, 0)$, $(0, 0, \pm c)$ |
Sections | Vertical traces: Hyperbola $ \dfrac{x^2}{a^2} – \dfrac{z^2}{c^2} = 1$, when $y =0$ $ \dfrac{y^2}{a^2} – \dfrac{z^2}{c^2} = 1$, when $x =0$ Horizontal traces: Ellipse $ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$, when $z =0$ |
Symmetry | All coordinate planes |
Center | The origin unless equation is shifted with respect to $x$, $y$, or $z$. |
Hyperboloid With Two Sheets: $\boldsymbol{\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2} –\dfrac{z^2}{c^2}= -1}$
The hyperboloid with two sheets looks like a 3D hyperbola separated in space, hence its distinct property. The general of this quadric surface is similar to that of hyperboloids with one sheet, but this time, we have $\boldsymbol{-1}$ on the right-hand side.
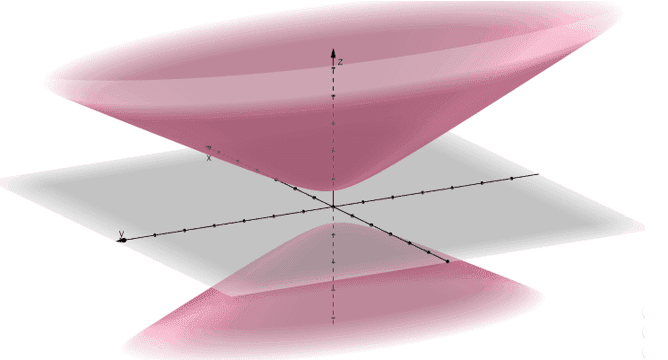
This hyperboloid of two sheets has the $z$-axis as its axis of symmetry. Here are the general forms for the hyperboloid of two sheets:
- Axis of symmetry at the $x$-axis: $\dfrac{x^2}{a^2}+ \dfrac{z^2}{c^2} –\dfrac{y^2}{b^2}= -1$.
- Axis of symmetry at the $y$-axis: $\dfrac{z^2}{c^2}+ \dfrac{y^2}{b^2} –\dfrac{x^2}{a^2}= -1$.
When $z = k$, the horizontal traces of the hyperboloid with two sheets will be ellipses. This will be true when $k > c$ or $k < -c$. As expected, the vertical traces of the quadric surface will be hyperbolas, as shown below.
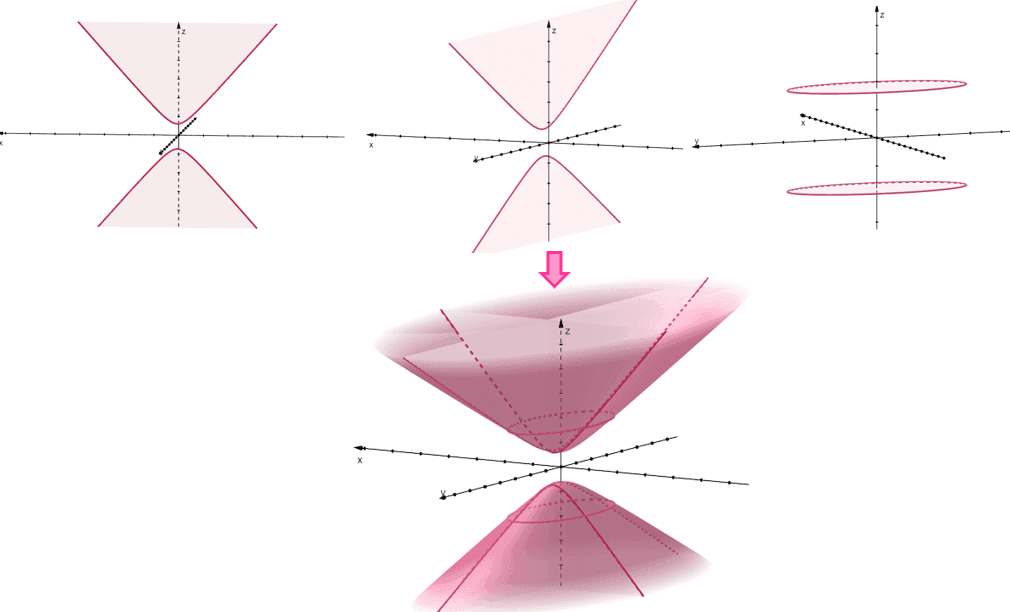
Here are some interesting properties of hyperboloid of two sheets
Intercepts | $(0, 0, \pm c)$ |
Sections | Vertical traces: Hyperbola $ \dfrac{x^2}{a^2} – \dfrac{z^2}{c^2} = -1$, when $y =0$ $ \dfrac{y^2}{b^2} – \dfrac{z^2}{c^2} = -1$, when $x =0$ Horizontal traces: Ellipse $ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = -1$, when $z =k$, $k > c$ or $k < =-c$ |
Symmetry | All coordinate planes |
Center | The origin unless equation is shifted with respect to $x$, $y$, or $z$. |
Once you’re familiar with shape, general forms, and properties of these six quadric surfaces, identifying them will be easy! Now, let’s see how we can use these properties to graph quadric surfaces.
How To Graph Quadric Surfaces?
We can graph quadric surfaces by using their traces, intercepts, and other properties that are easy to take note of given their second-degree equations.
Here’s a guideline that can help you in graphing different quadric surfaces:
- Rearrange the equation in standard form to identify the shape of the quadric surface.
- Find the traces of the quadric surface by seeing what happens when $x = 0$, $y = 0$, and $z =0$.
- If you know the traces from our previous section discussion, use that to double-check your answer.
- Graph these traces on the three-dimensional coordinate system.
- Sketch the quadric surface using what you know from the first step.
The best way to master the steps is by graphing different quadric surfaces using the second-degree equation representing the surface. Let’s try graphing $\dfrac{x^2}{4} + \dfrac{y^2}{16} + \dfrac{z^2}{9} = 1$ first.
\begin{aligned}\dfrac{x^2}{4} + \dfrac{y^2}{16} + \dfrac{z^2}{9} &= 1\\\dfrac{x^2}{2^2} + \dfrac{y^2}{4^2} + \dfrac{z^2}{3^2} &= 1\\&\Rightarrow \textbf{Ellipsoid}\end{aligned}
This quadric surface represents an ellipsoid, so we expect its graph to have ellipses in its $xz$, $yz$, and $xy$-planes. Find the equation of the traces by letting 1) $y = 0$, 2) $x = 0$, and 3) $x = 0$.
- Trace on the $xz$-plane: when $y = 0$, $\dfrac{x^2}{4} + \dfrac{z^2}{9} = 1$.
- Trace on the $yz$-plane: when $x = 0$, $\dfrac{y^2}{16} + \dfrac{z^2}{9} = 1$.
- Trace on the $xy$-plane: when $z = 0$, $\dfrac{x^2}{4} + \dfrac{y^2}{16} = 1$.
Ellipsoids will have six intercepts at $(\pm a, 0, 0)$, $(0, \pm b, 0)$, and $(0, 0, \pm c)$, so for our ellipsoid, it will have intercepts at $(\pm 2, 0, 0)$, $(0, \pm 4, 0)$, and $(0, 0, \pm 3)$. Let’s sketch these components to guide us in graphing the ellipsoid that is represented by $\dfrac{x^2}{4} + \dfrac{y^2}{16} + \dfrac{z^2}{9} = 1$.
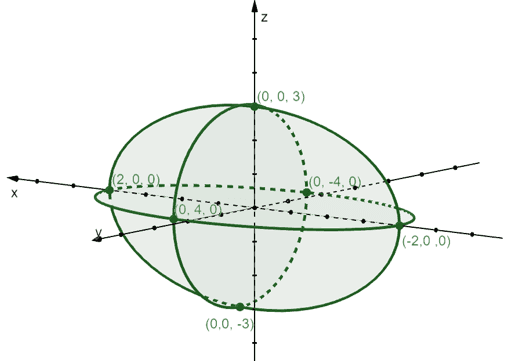
Now that we have these components, use what you know about the ellipsoid’s shape to graph the quadratic surface, as shown below.
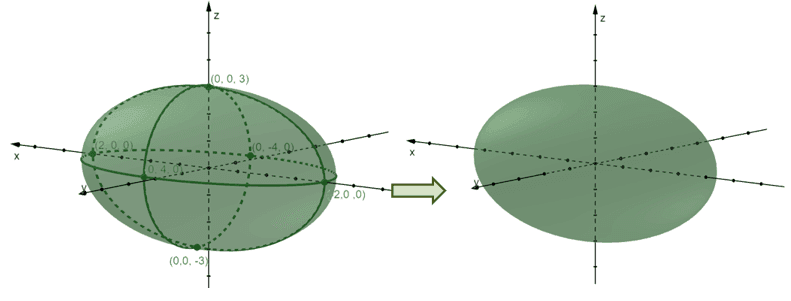
You can take out the components for a much “cleaner” look for the quadratic surface. But as you can see from our final graph, the ellipsoid is centered at the origin. We can also confirm that it is symmetric along the three coordinate planes.
Apply a similar process when graphing other quadric surfaces. Review the properties and general forms of the six quadric surfaces, and when you’re ready, head over to the section below to try out more problems on quadric surfaces!
Example 1
Rewrite $-4x^2+ y^2 + z^2 = 36$ then identify the quadric surface it represents.
Solution
Let’s first work on $-4x^2 +y^2 + z^2 = 36$ by dividing both sides of the equation by $36$.
\begin{aligned}-4x^2 + y^2 + z^2 &= 36\\ -\dfrac{x^2}{9} + \dfrac{y^2}{36} + \dfrac{z^2}{36} &= 1\end{aligned}
Rearrange the equation so that $-\dfrac{x^2}{9}$ is the last term on the left-hand side of the equation.
\begin{aligned} \dfrac{y^2}{36} + \dfrac{z^2}{36} – \dfrac{x^2}{9}&= 1\\\dfrac{y^2}{6^2} + \dfrac{z^2}{6^2} – \dfrac{x^2}{3^2}&= 1\end{aligned}
This represents the equation of a hyperboloid of one sheet that has an axis of symmetry at the $x$-axis.
Example 2
Sketch the quadric surface, $x^2 + \dfrac{y^2}{9} = \dfrac{z}{2}$.
Solution
First, let’s identify the type of quadric surface that the equation represents. Recall that the general form of elliptic paraboloids is $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = \dfrac{z}{c}$.
\begin{aligned} x^2 + \dfrac{y^2}{9} &= \dfrac{z}{2}\\ \dfrac{x^2}{1^2}+ \dfrac{y^2}{3^2} &= \dfrac{z}{2}\\&\Rightarrow \textbf{Elliptic Paraboloid} \end{aligned}
For elliptic paraboloids (with the axis of symmetry at the $z$-axis), we’re expecting parabolas as vertical traces and ellipses as horizontal traces.
- When $x = 0$, $ \dfrac{y^2}{9} = \dfrac{z}{2}$.
- When $y =0$, $x^2 = \dfrac{z}{2}$.
- When $z =0$, $x^2 + \dfrac{y^2}{9} = 0$.
Sketch these traces first to guide us in graphing the elliptic paraboloid.
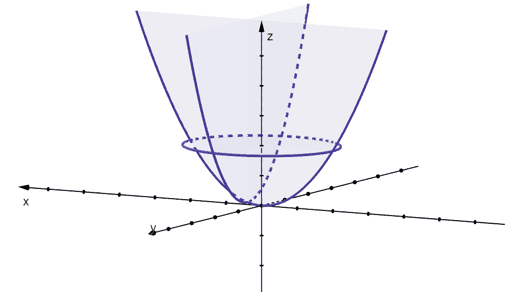
Now, we can use these cross-sections to graph the elliptic paraboloid. As we know, this quadric surface just looks like a three-dimensional parabola.
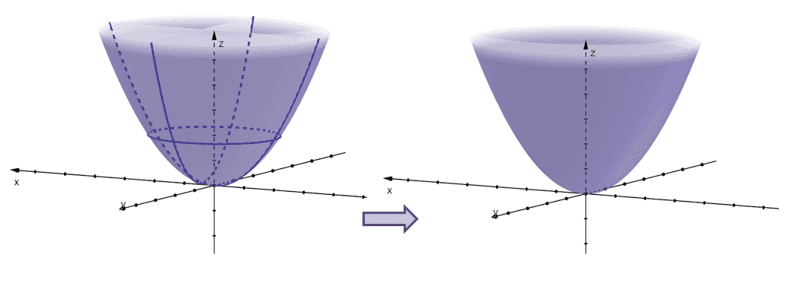
Here’s the graph of the elliptic paraboloid centered at $(0, 0, 0)$ that are symmetric about the $xz$ and $yz$-planes.
Practice Questions
1. Rewrite the following equations then identify the quadric surface they represent.
a. $12x^2- y^2 +4z^2 = 36$
b. $x^2 + 6y^2 +12z^2 – 48 = 0$
c. $9x^2 -18x +4y^2 +16y -36z +25 = 0$
2. Sketch the quadric surface, $x^2 + 2y^2 -\dfrac{z^2}{4} = 1$. Include at least three traces in your graph.
3. Sketch the quadric surface, $\dfrac{x^2}{4} +\dfrac{ y^2}{9} -\dfrac{ z^2}{16} = -1$
. Include at least three traces in your graph.
4. Sketch the quadric surface, $\dfrac{ z^2}{9} = x^2 +\dfrac{y^2}{4}$. Include at least three traces in your graph.
Answer Key
1.
a. Hyperboloid of one sheet
b. Ellipsoid
c. Elliptic paraboloid
2.
Traces of the Hyperboloid of One Sheet | |
When $z =0$: \begin{aligned}x^2 +2y^2 = 1\end{aligned} | When $z=\pm 2$: \begin{aligned}x^2 + 2y^2 = 2\end{aligned} |
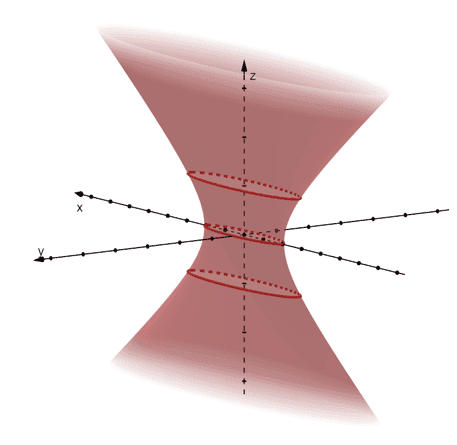
3.
Traces of the Hyperboloid of Two Sheets | |
Vertical traces: \begin{aligned} \dfrac{x^2}{4}-\dfrac{ z^2}{16} &= -1\\ \dfrac{y^2}{4}-\dfrac{ z^2}{16} &= -1\end{aligned} | Horizontal traces (when $z = 5$): \begin{aligned}\dfrac{x^2}{4} + \dfrac{ y^2}{9} &= 24\end{aligned} |
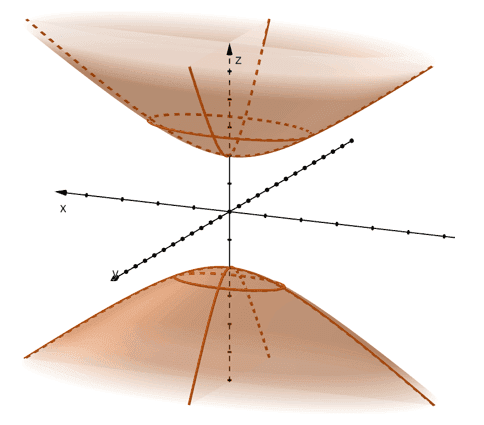
4.
Traces of a Cone | |
Vertical traces (when $x=1$ and $y=2$): \begin{aligned} \dfrac{z^2}{9} – \dfrac{y^2}{4} &=1\\\dfrac{z^2}{9} – x^2 &= 1\end{aligned} | Horizontal traces (when $z= \pm3$): \begin{aligned}x^2 +\dfrac{ y^2}{4} &= 1\end{aligned} |
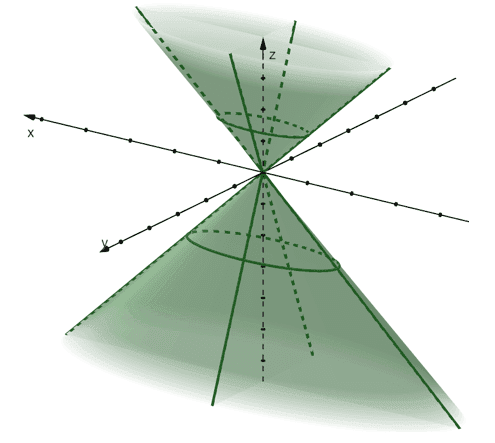
Images/mathematical drawings are created with GeoGebra.
