Ratios – Explanation & Examples

In a classroom, there are 60 girls and 40 boys. How can we can represent the number of girls to the number of boys and vice versa? In another case also, 2 kg of rice and 3 kg of beans are used to prepare a meal, how can we represent the weight of the rice to the weight of beans in the meal? Such kind of situations raises the need of ratios.

Ratios are frequently used in our daily life to simplify problems by expressing numbers into their correct perspective.

Below are some of the applications of ratios:

• Ratios are applied when converting from one currency to another. For example, you can convert Pounds to Euros or to Dollars by using ratios.
• Winnings on a bet are calculated using a ratio.
• You can use ratios to calculate the number of bottles of drinks you need for a party.
• Ratios can used in a recipe to prepare a certain meal.

The origin of the ratio is not very well known. There are many examples of ratios where the people are applying it in their daily lives but unaware of it.

For example, when there were tribes, they use to count like one tribe is twice as large as another. When we talk about the Greek writers, Nicomachus used ratio in arithmetic, Eudoxus used in geometry, and Smyrna in the chapter on music.

What is a Ratio?

In mathematics, a ratio is defined as a tool used to compare the size of two or more quantities in relation to each other. Ratios allow us to measure and express quantities by making them easier to interpret.

A ratio is a kind of a fraction where the numerator is referred to as antecedent and the denominator is termed as the consequent. We use a colon symbol (:) to denote a ratio. For instance, 3: 4, 1: 3, 5:7, 1:1, etc. are examples of ratios.

Let us take a look at some of the properties of ratios.

• Ratios only represent quantities of the same unit.
• Ratios are dimensionless.
• The first item in the sentence comes first in a ratio.
• Equivalent ratios have equivalent corresponding fractions.
• In the ratio such as a: b, a is the antecedent and b is the consequent
• The positions of antecedent and consequent in a ratio cannot be interchanged.
• Ratios can be used to represent multiple quantities. For example, a: b: c: d…

How to Calculate Ratio?

There several different ways of calculating a ratio. One the most common method is comparing two quantities is using a colon. For example, if there are 20 boys and 30 girls in a classroom. The ratio of boys to girls can be represented as 20: 30 which simplifies to 2:3.

Another method of calculating the ratio is by expressing the quantities as a fraction. The first quantity is usually represented as the numerator while the second quantity represents the denominator. For example, the ratio of boys to girls can as well be represented as 2/3.

Other methods of finding the ratio between numbers include the use the word “to” between the numbers themselves and calculating a ratio in decimal form. For example, a ratio 3:10 can be expressed as 3 to 10 and 0.3 in decimal format.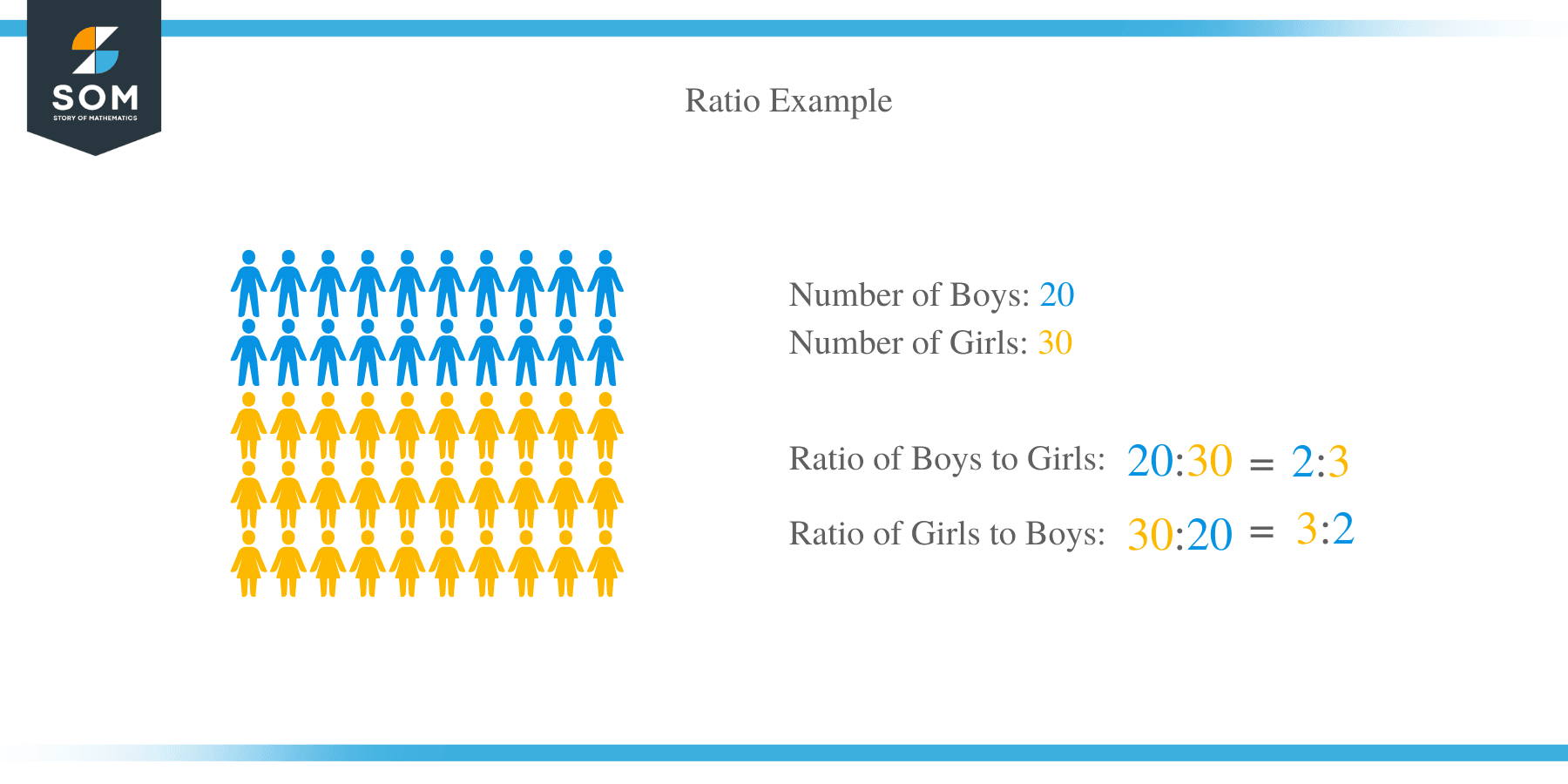

Examples

Instrument type

A component is composed 30% copper, 60% brass and 10% gold. Use this information to calculate:

• Ratio of copper to brass

Copper = 30%

Brass = 60%

Copper to brass = 30: 60 which simplifies to 1:2 or 1/2

• Ratio of gold to brass

Gold = 10%

Brass = 60%

Ratio of gold: brass = 10:60, which simplifies 1:6 or 1/6

• Ratio of gold to copper

Gold =10%

Copper = 30%

Ratio of gold: copper =10:30, which simplifies to 1:3 or 1/3

• Ratio of copper: brass: gold = 30: 60:10= 3:6:1(in simplified form)
• Ratio of copper to the total = 30:100 = 3: 10 or 3/10

Simplifying Ratios

A ratio can be simplified in its lowest terms possible no matter how it is expressed. This is possible by finding the greatest common factor between the numbers. For instance, the ratio 12 to 16 can simplified as follows:

Divide both numbers 12 and 16 by the greatest common factor 4. Therefore 12: 16 is written as:

• 3:4
• 3/4
• 3 to 4
• 0.75