- Home
- >
- Rectangular form – Definition, Example, and Explanation
JUMP TO TOPIC
Rectangular Form – Definition, Example, and Explanation
 The rectangular form of complex numbers is the first form we’ll encounter when learning about complex numbers. This form depends on its Cartesian coordinate, and you’ll actually learn why in the next section.
The rectangular form of complex numbers is the first form we’ll encounter when learning about complex numbers. This form depends on its Cartesian coordinate, and you’ll actually learn why in the next section.
Rectangular forms of complex numbers represent these numbers highlighting the real and imaginary parts of the complex number.
Basic operations are much easier when complex numbers are in rectangular form. It’s more intuitive for us to graph complex numbers in rectangular form since we’re more familiar with the Cartesian coordinate system.
This article will refresh our knowledge on:
- The components that make up a complex number.
- Graphing complex numbers on a complex plane.
- Converting complex numbers in the rectangular form to polar form, and the other way around.
- Manipulating complex numbers in rectangular form.
Make sure to pull up your notes and review these concepts as we’ll be needing them as we learn more about complex numbers in rectangular form.
What is rectangular form?
The rectangular form is based on its name – a rectangular coordinate system. This means that these are complex numbers of the form $z = a + bi$, where $a$ is the real part, and $bi$ represents the imaginary part. Here are some examples of complex numbers in rectangular form.
- $-3 + 4i$ : $-3$ represents the real number part while $4i$ represents the imaginary part.
- $-6i$: This is an imaginary number that only contains an imaginary part, $-6i$.
- $5$: Since $5$ is a counting number and consequently, a real number, $5$ is still a complex number with its imaginary number part equal to $0$.
Complex numbers of the form $a + bi$ can be graphed on a complex plane simply by plotting $(a,b)$, where $a$ is the coordinate for the real axis and $b$ is the coordinate for the imaginary axis.
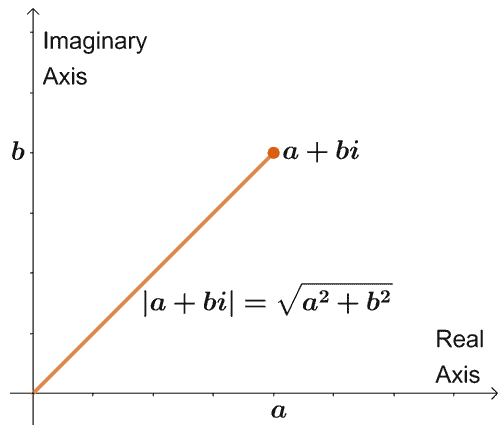
Here’s a graph of how $a + bi$ is graphed on a complex plane. As mentioned, $a$ represents the distance along the real axis, and $b$ represents the distance along the imaginary axis – a similar approach when we graph rectangular coordinates.
The distance formed by $a + bi$ from the origin is equal to $\sqrt{a^2 + b^2}$ or also known as the modulus or the absolute value of the complex number.
How to convert rectangular form?
As mentioned, rectangular form is the first form of complex numbers that we’ll be introduced to, but complex numbers can also be rewritten in their trigonometric or polar forms.
| Rectangular Form | Polar Form |
| $-3 + 3i$ | $3\sqrt{2}(\cos 135^{\circ} + i\sin135^{\circ})$ |
| $-2\sqrt{3} – 2i$ | $4(\cos 210^{\circ} + i\sin 210^{\circ})$ |
| $4 – 4i$ | $4\sqrt{2}(\cos 315^{\circ} + i\sin 315^{\circ})$ |
| $5 + 5\sqrt{3}i$ | $10(\cos 60^{\circ} + i\sin 60^{\circ})$ |
These are just some examples of pairs of complex numbers in their two forms: rectangular and polar forms. Let’s refresh what we’ve learned about writing complex numbers in these two forms.
How to convert rectangular form to polar form?
We’ve thoroughly discussed converting complex numbers in rectangular form, $a + bi$, to trigonometric form (also known as the polar form). Make sure to review your notes or check out the link we’ve attached in the first section.
This section will be a quick summary of what we’ve learned in the past:
- Find the modulus, $r = \sqrt{a^2 + b^2}$, of the complex number.
- Determine the argument, $\theta = \tan^{-1} \dfrac{b}{a}$, and make sure we choose the angle that lies on the right quadrant.
- Use these values and write the complex number of the form $r(\cos \theta + i\sin \theta)$.
How to convert polar form to rectangular form?
Changing complex numbers in polar form is much easier since it requires us to only evaluate cosine and sine at different values of $\theta$.
- When given complex number of the form $r(\cos \theta + i\sin \theta)$, evaluate the values of $\sin \theta$ and $\cos \theta$.
- Distribute $r$ to each of the evaluated values of $\cos \theta$ and $i\sin \theta$.
- Make sure to return the values of the form, $a + bi$.
Don’t worry. We’ve prepared some examples for you to work on to practice your knowledge of converting complex numbers in polar form.
Summary of rectangular form definition and properties
Why don’t we recap what we’ve learned so far about complex numbers in the rectangular form before diving into the different problems we’ve prepared?
- The general rectangular (or standard) form of the complex numbers is $a + bi$.
- We can convert complex numbers in rectangular form, by finding $r = \sqrt{a^2 + b^2}$ and $\theta = \tan^{-1} \dfrac{b}{a}$.
- Don’t forget, when working with equations involving complex numbers, the real number parts and imaginary number parts must be equal for the equation to be valid.
We can also do many things when given a complex number in rectangular form, and we’ve listed some that we’ve learned in the past. Don’t have your handy notes with you? No worries, we’ve added a few links for you to check out as well.
- It’s easier to add and subtract complex numbers in rectangular form since we combine the real and imaginary number parts.
- Yes, we can also multiply and divide complex numbers in rectangular form through algebraic manipulation.
- The product of a $a + bi$ and its conjugate, $a – bi$, is equal to $a^2 + b^2$, which can help simplify the quotient of two complex numbers.
Let’s apply everything that we’ve learned from this article and try out these sample problems.
Example 1
Graph the following complex numbers on the complex plane and include their corresponding absolute value number.
a. $6 – 6i$
b. $-4\sqrt{3} – 4i$
c. $-5i$
Solution
Since we also need the absolute value number of these three complex numbers, why don’t we start with that using the fact that $|a + bi| = \sqrt{a^2 + b^2}$?
| $\boldsymbol{a + bi}$ | $\boldsymbol{|a + bi| }$ |
| $6 -6i$ | $\sqrt{(6)^2 + (-6)^2} = 6\sqrt{2}$ |
| $-4\sqrt{3} -4i$ | $\sqrt{(-4\sqrt{3})^2 + (-4)^2} = 8$ |
| $-5i$ | $\sqrt{(0)^2 + (-5)^2} = 5$ |
Now that we have the absolute value of the three complex numbers let’s graph the three complex numbers on one complex plane.
- For $6 – 6i$, graph the coordinate $(6, -6)$ or $6$ units to the right and along the real axis and six units downward and along the imaginary axis.
- Similarly, we can graph $-4\sqrt{3} – 4i$ by plotting $(-4\sqrt{3}, -4)$ on the complex plane.
- Since $-5i$ only contains an imaginary number part, we graph $-5i$ on the imaginary axis and should be found $5$ units below the real axis.
Connect each complex number to the origin and label the segment with the corresponding absolute value number.
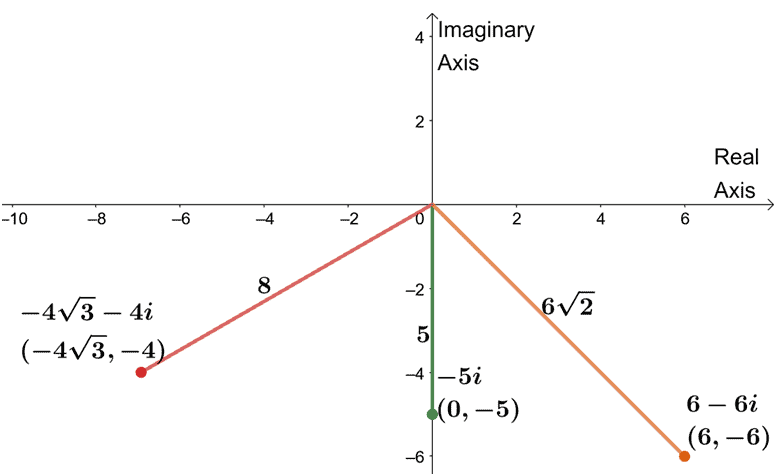
Example 2
Evaluate the following operations on the following complex numbers.
a. $(8 – 8i) + (-6 + 12i)$
b. $(-3\sqrt{3} + 5i) – (4\sqrt{3} – 6i)$
c. $(-4 + 2i)(-2 – i) + (2- 3i)$
Solution
Recall that adding and subtracting complex numbers is similar to adding and subtracting binomials. We combine the terms with the real numbers and imaginary numbers. It’s the same way that we combine “like terms.”
Let’s work on the first item first: $(8 – 8i) + (-6 + 12i)$.
$\begin{aligned} (8 – 8i) + (-6 + 12i) &= [8 + (-6)] + (-8 + 12)i\\&= 2 + 6i\end{aligned}$
Make sure to distribute the negative sign carefully when subtracting two complex numbers.
$\begin{aligned} (-3\sqrt{3} + 5i) – (4\sqrt{3} – 6i) &=-3\sqrt{3} + 5i – 4\sqrt{3} -(-6i)\\&= -3\sqrt{3} + 5i – 4\sqrt{3} + 6i\\&= (-3\sqrt{3} – 4\sqrt{3}) + (5 + 6)i\\&=-7\sqrt{3} + 11i \end{aligned}$
For the third item, multiply the two complex numbers first.
- Apply the FOIL method to distribute the terms.
- Replace $i^2$ with $-1$.
- Combine real and imaginary number parts.
$\begin{aligned} (-4 +2i)(-2 – i) &= (-4)(-2)+ (-4)(-i) + (2i)(-2) + (2i)(-i)\\&=8 + 4i – 4i- 2i^2\\&=8 + 4i – 4i -2(-1)\\&=8 + 4i – 4i + 2\\&= (8 + 2) + (4 -4)i\\&=10 \end{aligned}$
Replace $(-4 + 2i)(-2 – i)$ with its product then simplify the expression further.
$\begin{aligned} (-4 +2i)(-2 – i) + (2 – 3i) &= 10 + (2 – 3i)\\&= (10 + 2) – 3i\\&= 12 – 3i\end{aligned}$
Listing down the results for the three operations, we have the following:
a. $(8 – 8i) + (-6 + 12i) = 2 + 6i $
b. $(-3\sqrt{3} + 5i) – (4\sqrt{3} – 6i) = -7\sqrt{3} + 11i $
c. $(-4 + 2i)(-2 – i) + (2- 3i) = 12 – 3i $
Example 3
Convert the following complex numbers in polar form to rectangular form.
a. $-4(\cos 90^{\circ} + i\sin 90^{\circ})$
b. $6\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right)$
c. $-\sqrt{3} \text{cis } \dfrac{3\pi}{4}$
Solution
Evaluate the cosine and sine values inside the parenthesis when converting complex numbers to rectangular form. Distribute the modulus into each of the values inside to simplify the expression to a form, $a +bi$.
Starting with $-4(\cos 90^{\circ} + i\sin 90^{\circ})$, $\cos 90^{\circ} = 0$ and $\sin 90^{\circ} = 1$. Replace the terms inside the parenthesis with these values then distribute $-4$.
$\begin{aligned} -4(\cos 90^{\circ} + i\sin 90^{\circ}) &= -4(0 + i)\\&=0 – 4i\\&= -4i\end{aligned}$
The second item will require us to perform a similar process, but this time, we’re working with angles in terms of $\pi$. Recall that $\cos \dfrac{\pi}{3} = \dfrac{1}{2}$ and $\sin \dfrac{\pi}{3}= \dfrac{\sqrt{3}}{2}$.
$\begin{aligned} 6\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right) &= 6\left( \dfrac{1}{2} + i\dfrac{\sqrt{3}}{2}\right)\\&=6 \cdot \dfrac{1}{2} – 6 \cdot i \dfrac{\sqrt{3}}{2}\\&= 3 – 3\sqrt{3}i\end{aligned}$
For the third item, make sure to rewrite $r \text{cis } \theta$ as $r(\cos \theta + i \sin \theta)$.
$\begin{aligned} -\sqrt{3} \text{cis } \dfrac{3\pi}{4} &= -\sqrt{3}\left(\cos \dfrac{3\pi}{4} + i\sin \dfrac{3\pi}{4}\right)\\ &= -\sqrt{3}\left( -\dfrac{\sqrt{2}}{2} + i\dfrac{\sqrt{2}}{2}\right)\\&=-\sqrt{3} \cdot -\dfrac{\sqrt{2}}{2} – \sqrt{3} \cdot i \dfrac{\sqrt{2}}{2}\\&= \dfrac{\sqrt{6}}{2}-i\dfrac{\sqrt{3}}{2}\end{aligned}$
Hence, we have the following complex numbers in their rectangular forms:
a. $-4(\cos 90^{\circ} + i\sin 90^{\circ}) = -4i$
b. $6\left(\cos \dfrac{\pi}{3} + i\sin \dfrac{\pi}{3}\right) = 3 – 3\sqrt{3}i$
c. $-\sqrt{3} \text{cis } \dfrac{3\pi}{4} = \dfrac{\sqrt{6}}{2}-i\dfrac{\sqrt{3}}{2}$
Practice Questions
![]()
Open Problem
Graph the following complex numbers on the complex plane and include their corresponding absolute value number.
a. $-5 – 5i$
b. $-12i$
c. $2\sqrt{3} – 2i$
Open Problem Solution
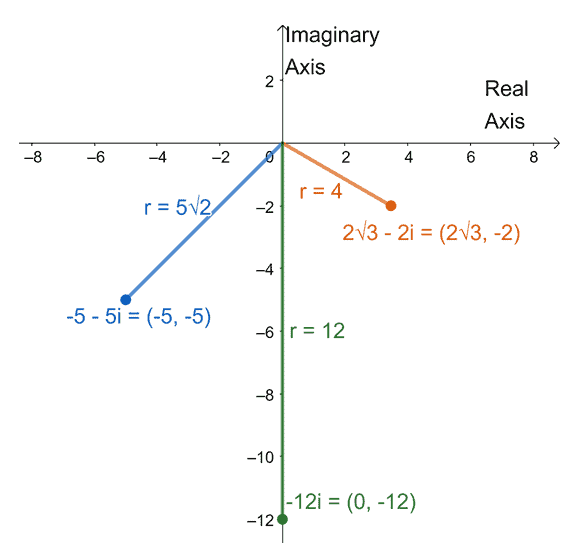
Images/mathematical drawings are created with GeoGebra.
