Reference Angle – Explanation and Examples

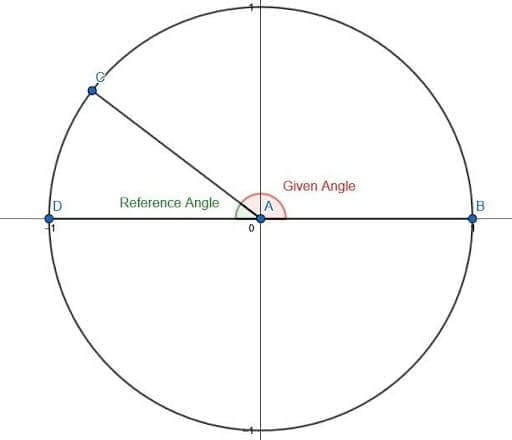
A reference angle is an acute angle between a given angle’s terminal ray and the x-axis.

Reference angles are always positive, and an angle’s reference angle can be itself.

Reference angles are useful in trigonometry and sciences that make use of it, such as astronomy, architecture, and engineering.

Before moving forward with this section, make sure to review angles and trigonometric functions.

What Is a Reference Angle?

A reference angle is a positive acute angle or right angle. Each angle has a reference, which can be found by locating an acute angle formed by the terminal angle of the given angle and the x-axis. This means that an acute angle or a right angle is its own reference angle.

Reference angles make it easier to calculate trigonometric ratios for obtuse and reflex angles by relating them to a smaller range of angles. This makes memorizing common trigonometric ratios for angles between the zero angle and a right angle sufficient for memorizing all possible angles.

Obtuse Angles

When the given angle is obtuse, its measure is greater than $90$ degrees ($\frac{\pi}{2}$ radians) and less than $180$ degrees (\pi radians).

Now, the reference angle for an obtuse angle is easy to visualize using the unit circle. This is the angle formed by the terminal side of the obtuse angle and the ray extending to the left along the horizontal axis.

To find this angle algebraically, subtract the given angle from $180$ degrees or $\pi$ radians. Remember that this angle is always given as a positive angle.

Reflex Angles

Recall that reflex angles are angles greater than $180$ degrees but less than $360$ degrees.

For a reflex angle between $180$ and $270$ degrees ($\pi$ and $\frac{3\pi}{2}$ radians), the reflex angle is the angle formed by the given angle’s terminal side and the ray extending left along the x-axis. For an angle between $270$ and $360$ degrees ($\frac{3\pi}{2}$ and $2\pi$ radians), it is the angle formed by the terminal angle and the ray extending to the right along the x-axis.

Therefore, the formulas for these angles are $\alpha-180$ degrees or $\alpha-\pi$ radians for angles, $\alpha$ between $180$ and $270$ degrees, or between $\pi$ and $\frac{3\pi}{2}$ radians.

For given angles, $\beta$ between $270$ and $360$ degrees or $\frac{3\pi}{2}$ and $2\pi$ radians, the reference angle is $360-\beta$ or $2\pi-\beta$.

Angles Greater Than a Full Angle

For angles greater than a full angle or for negative angles, find the coterminal standard angle between $0$ and $360$ degrees or $0$ and $2\pi$ radians. Then, find the reference angle for this standard angle.

How To Find the Reference Angle

Based on this, the formula for finding the reference angle, $\gamma$ degrees, for a given angle of $\alpha$ degrees varies depending on the value of $\alpha$.

• $\gamma =  \alpha$ for $0 \leq \alpha \leq 90$ degrees
• $\gamma = 180-\alpha$ for $90 < \alpha \leq 180$ degrees
• $\gamma = \alpha-180$ for $180 < \alpha \leq 270$ degrees
• $\gamma = 360-\alpha$ for $270 < \alpha < 360$ degrees.

When $\gamma$ and $\alpha$ are in radians, these formulae are:

• $\gamma =  \alpha$ for $0 \leq \alpha \leq \frac{\pi}{2}$ radians
• $\gamma = \pi-\alpha$ for $\frac{\pi}{2} < \alpha \leq \pi$ radians
• $\gamma = \alpha-\pi$ for $\pi < \alpha \leq \frac{3\pi}{2}$ radians
• $\gamma = 360-\alpha$ for $\frac{3\pi}{2} < \alpha < 2\pi$ radians.

Reference Angles in Trigonometry

Note that memorizing the trigonometric ratios for every single angle is a lot! Using trigonometric identities and reference angles, however, means one can memorize at least the major ratios between the $0$ angle and a right angle and know many other ratios.

For example, suppose someone knew the sine and cosine ratios for just two angles measuring $45$ degrees and $30$ degrees. This person also knows the sum and difference identities, namely:

$sin{(\alpha \pm \beta)} = sin{\alpha}cos{\beta} \pm cos{\alpha}sin{\beta}$

And

$cos{(\alpha + \beta)} = cos{\alpha}cos{\beta} – sin{\alpha}sin{\beta}$

Then, they would also know the trig ratios for angle measuring $30+45 = 75$, $45-30 = 15$,  and$45+45+30 = 130$ degrees, for example.

If such a person also knew the sine and cosine for a straight angle, he or she could then use reference angles to find $180-45 = 135$ degrees or $180-75=105$ degrees.

This opens up a lot of possibilities with very little memorization.

Additionally, the identities $sin{(-\theta)} = -sin(\theta)$ and $cos{(-\theta)} = cos(\theta)$ open up calculations for negative numbers.

Examples

This section goes over common examples of problems involving reference angles and their step-by-step examples.

Example 1

Given that the sine and cosine of $45$ degrees angles are both $\frac{1}{\sqrt{2}}$, find the sine of $135$ degrees.

Solution

Recall the formulas for sine and cosine:

$sin{(\alpha \pm \beta)} = sin{\alpha}cos{\beta} \pm cos{\alpha}sin{\beta}$

$cos{(\alpha + \beta)} = cos{\alpha}cos{\beta} – sin{\alpha}sin{\beta}$.

Therefore, finding the sine of $135 = 45+45+45$ requires first finding $sin90$ and $cos90$.

$sin{(45 + 45)} = sin{45}cos{45} + cos{45}sin{45}$

Substituting, this is:

$\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2}}$

Then, simplifying, this is:

$\frac{1}{2}+\frac{1}{2} = 1$.

For cosine of $90$:

$cos{(45+45)} = cos{45}cos{45} – sin{45}sin{45}$.

Now, this simplifies to:

$cos{90} = \frac{1}{2} – \frac{1}{2}$.

Therefore, $sin135$ is:

$sin{45}cos{90} + cos{45}sin{90}$.

Finally, this simplifies to:

$\frac{1}{\sqrt{2}}\times0 + \frac{1}{\sqrt{2}}\times1 = \frac{1}{\sqrt{2}}$.

Example 2

Note that the sine of a $30$ degree angle is $\frac{1}{2}$, and the cosine of a $30$ degree angle is $\frac{\sqrt{3}}{2}$.

Given this information, find the cosine of $75$ degrees.

Solution

Note that cosine and sine of $45$ degrees were given in example 1. Therefore, cosine of $75$ degrees is equal to:

$cos{30+45} = cos{30}cos{45}-sin{30}sin{45}$.

Substituting, this is:

$\frac{\sqrt{3}}{2}\times\frac{1}{\sqrt{2}} – \frac{1}{2}\times\frac{1}{\sqrt{2}}$.

Simplifying, this becomes:

$\frac{\sqrt{3}}{2\sqrt{2}} – \frac{1}{2\sqrt{2}}$.

As one fraction, this is:

$\frac{\sqrt{3}-1}{2\sqrt{2}}$.

Example 3

Sine of a straight angle is $0$, and the cosine of a straight angle is $-1$.

Find the cosine of $105$ degrees.

Solution

This problem builds off of the previous two.

Since $105=180-75$, this problem involves finding:

$cos{180-75} = cos{180}cos{75} + sin{180}sin{75}$.

Since this is the cosine of the difference of angles, the minus sign on the right side of the equation becomes a plus sign.

This is:

$-1\times\frac{\sqrt{3}-1}{2\sqrt{2}} + 0\times sin{75}$.

This simplifies to:

$-\frac{\sqrt{3}-1}{2\sqrt{2}}$.

Therefore, $cos{105} = -cos{75}$.

Example 4

Describe how to use sine and cosine of the angles $30$, $45$, and $180$ to find the tangent of an angle measuring $165$ degrees.

Solution

An angle of $165$ degrees is equal to:

$180-(45-30)$.

Therefore, find the sine and cosine of $15$ degrees. Then, use these to find the sine and cosine of $180-15 = 165$ degrees.

Finally, divide the sine of $165$ degrees by the cosine of $165$ degrees.

Example 5

Find the cosecant of an angle with a measure of $120$ degrees.

Solution

Recall first that cosecant is equal to $\frac{1}{sinx}$.

Then, note that $120 = 45+45+30$.

Therefore, finding the cosecant of $120$ degrees requires finding the sine of $120$ degrees, which can be found using the sine of $45$ and $30$.

Since, however, the sine of $90$ was given in example 2, this is $90+30$.

Therefore, sine of $120$ is:

$sin{90+30} = sin{90}cos{30} + sin{30}cos{90}$.

This then simplifies to:

$1\times \frac{\sqrt{3}}{2} +\frac{1}{2} \times 0$.

Therefore, the sine is:

$\frac{\sqrt{3}}{2}$.

Thus, this means the cosecant is the reciprocal:

$\frac{2}{\sqrt{3}}$ or $\frac{2\sqrt{3}}{3}$.