Related rates – Definition, Applications, and Examples

Learning how to solve related rates of change problems is an important skill to learn in differential calculus. This has extensive application in physics, engineering, and finance as well.

In our discussion, we’ll also see how essential derivative rules and implicit differentiation are in word problems that involve quantities’ rates of change. In fact, related rates will help us when we want to solve problems that involve two or more related quantities that are changing over time.

Related rates problems are problems that involve two or more quantities and their corresponding rates of change with respect to time. The relationship between these quantities is used to express their related rates in terms of the other quantities’ known rate of change.

As we have mentioned, this topic is an application of what we have learned so far, so make sure you’re ready with your knowledge on the following:

• Finding the derivative of functions using the derivative rules – that includes the chain rule.
• Know how to solve for unknown rates of change using implicit differentiation techniques.
• Since we’ll be dealing with word problems involving related rates, we’ll be applying some formulas and concepts from our precalculus classes.

Let’s begin by understanding when related rates are most helpful and how to know if the problem requires our knowledge of related rates.

What are related rates?

Related rates and problems involving related rates take advantage of quantities that are related to each other. Related rates help us determine how fast or how slow a certain quantity is changing using the rate of change of the second quantity.

Let’s take a look at the example shown below:

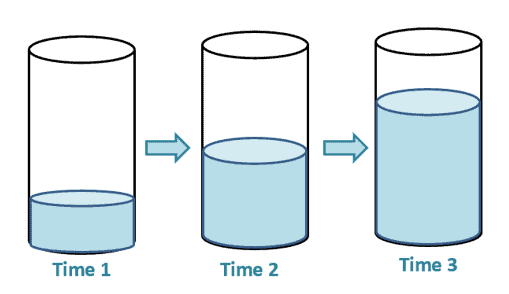
• As time progresses, the water level within the cylinder increases. This also means that the volume of the water inside will be varying with respect to time. We can use related rates here if we want to observe the rates of change of the water level’s height and volume with respect to time.
• We can assign $h$ to be the water’s height, so its rate of change will be $\dfrac{dh}{dt}$, where $dt$ represents the change in time, $t$.
• Similarly, if we assign $V$ to be the water’s volume, we can represent the volume’s rate of change as $\dfrac{dV}{dt}$.
• The two rates, $\dfrac{dh}{dt}$ and $\dfrac{dV}{dt}$, can then be used to determine unknown values or quantities.

Here are more examples of quantities that are related to each other:

Now that we understand how two or more quantities’ rates can be related to each other, let’s go ahead and apply this to solve problems involving related rates.

In problems that involve related rates, we expect at least one of the rates of changes to be given. This will simplify the process for you as well – don’t worry, we have allotted a separate section for us to focus on these helpful steps.

How to do related rates?

Now that we know how to relate quantities and find their rates of change in terms of time or some other common factor, let’s dive right into solving problems involving related rates. The steps below can guide you:

Step 1: Write down the quantities that are given and need to be determined.

Step 2: Make a sketch and include essential labels whenever possible.

Step 3: Construct an equation that relates both the constant and variable quantities.

Step 4: Apply implicit differentiation to differentiate the equation in terms of $t$ (or whatever common factor is shared).

Step 5: Substitute all the values that we have from Step 1 then find the unknown rate of change.

Step 6: Review the problem and make sure all the questions were answered.

Word problems involving related rates can be tricky at first and that’s because we’ll be dealing with different quantities. These quantities will have unique relationships and we might even need to recall important properties such as the following:

These are just some of the several quantities you might encounter when dealing with related rates. Don’t worry, most of the concepts that will be used have been discussed before! Why don’t we go ahead and solve the problem shown below using the six steps we’ve provided?

A ladder is sliding down along a vertical wall. The ladder is 20 meters long and the top of the ladder is slipping at a constant rate of 20 m/s. Using the information, determine how fast the bottom of the ladder is moving along the ground when the bottom is 12 meters from the wall.

Step 1-2: Write down the given and the value we need. Keep in mind that both distances will change depending on time, $t$.

Let’s draw a right triangle to represent the sliding ladder.

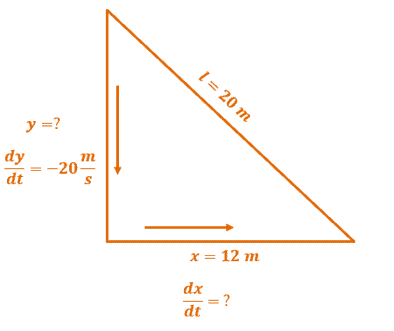
Step 3: Use the Pythagorean theorem, $c^2 = a^2 + b^2$, to set up an equating relating bot fixed and variable quantities. We can also use this to find $y$ when $x =12$.

\begin{aligned}l^2 &= x^2 + y^2\\20^2 &= x^2 + y^2\end{aligned}

\begin{aligned}20^2 &= (12)^2 + y^2\\400 &= 144 + y^2\\y^2 &= 256\\y&=16\end{aligned}

This means that when the ladder is $12$ meters from the wall and along the ground, it reaches a height of the wall for $16$ meters.

Step 4: Differentiate both sides of the equation using implicit differentiation. Apply the chain rule when differentiating $x^2$ and $y^2$ to account for $\dfrac{dx}{dt}$ and $\dfrac{dy}{dt}$.

\begin{aligned}400&= x^2 + y^2\\x^2+y^2&=400\\ {\color{Teal} 2x \cdot \dfrac{dx}{dt}} + {\color{Teal}2y\cdot \dfrac{dy}{dt}}&={\color{Orchid} 0},\phantom{x}{\color{Teal}\text{Power & Chain Rules}}\text{ , }{\color{Orchid} \text{Constant Rule}}\\2x \cdot \dfrac{dx}{dt}&= -2y \cdot \dfrac{dy}{dt}\end{aligned}

Step 5-6: Use the values of $x$ and $y$ from Step 1 and Step 3 then solve for the remaining unknown value.

\begin{aligned}2x \cdot \dfrac{dx}{dt}&= -2y \cdot \dfrac{dy}{dt}\\2(12)\dfrac{dx}{dt} &=-2(16)(-20)\\24\dfrac{dx}{dt}&= 640\\\dfrac{dx}{dt}&= \dfrac{80}{3}\end{aligned}

We’re looking for the speed at the horizontal distance changes per second. This represents $\dfrac{dx}{dt}$, so the ladder is sliding horizontally at $\dfrac{80}{3}$ meters per second.

What are the practical applications of related rates?

As we have mentioned in our introduction, related rates problems have an extensive application in physics, engineering, and other fields. That’s because researchers will have to compare two or more quantities’ behavior when they share common factors such as time.  Here are some practical applications of related rates:

• Observing the horizontal and vertical motions of space shuttles and their tracking cameras.
• Estimating the distance and speed of a docking boat from the shore.
• Calculating the rates of changes of an object’s kinetic energy or effective resistances.

These are just some of the many applications of related rates. We can also answer word problems involving related rates. This includes problems that involving expanding balloons and observing the balloon’s volume over time.

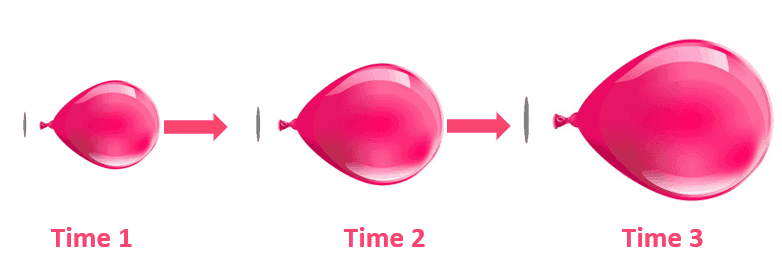
For this problem, the radius and the volume of the balloon are increasing as time increases. We can either determine the radius and volume’ rates of change through implicit differentiation.

Here are some more common problems you might encounter in your differential calculus classes:

• Observing the change between the height and distance from the wall of a falling ladder.
• Finding the volume inside when refilling a container or when a leaking container occurs.
• Measuring the length of a person’s shadow and the rate that it changes depending on the person’s distance from a lamppost.

Don’t worry, we’ve prepared more problems involving related rates in the section below. These problems will also help you refresh some essential precalculus topics, so this will be a great practice for you too!

Example 1

Samantha is walking home from her town’s library. Her distance from the library, in feet, after $t$ minutes is modeled by the differentiable function, $d’(t)$. Which of the following must be the units used to measure $d’(t)$?

a. Feet
b. Minutes
c. Feet per minute
d. Minutes per foot

Solution

Let’s write down the units used for each quantity given in the problem.

The function, $d’(t)$, represents the distance covered by Samantha over time.

\begin{aligned}d’(t) &= \dfrac{\text{Distance in Feet}}{\text{Time in Minutes}}\end{aligned}

c. This means that $d’(t)$’s unit can be measured in terms of feet per minute.

Example 2

Given that, $a$, $b$, and $c$ satisfy the equation, $a^2 = b^2 – 6b + c^2$, find $\dfrac{da}{dt}$ , if we have the following values:

• $a=4$,$b = -1$ and $c = -2$
• $\dfrac{db}{dt} = 4$ and $\dfrac{dc}{dt} = 3$

Solution

Find $\dfrac{da}{dt}$ through implicit differentiation and our fundamental derivative rules. Take the derivative of both sides of the equation with respect to $t$.

\begin{aligned}a^2 &= b^2-6b + c^2\\\dfrac{d}{dt}(a^2) &= \dfrac{d}{dt}(b^2-6b + c^2)\\ {\color{Teal}2a} {\color{Orchid}\cdot \dfrac{da}{dt}}&= {\color{Teal}\dfrac{d}{dt}(b^2)- \dfrac{d}{dt}(6b)+\dfrac{d}{dt}(c^2)},\phantom{x}{\color{Teal}\text{Power & Sum Rules}}\text{ , }\color{Orchid}\text{Chain Rule} \\2a\cdot \dfrac{da}{dt}&={\color{Teal}2b} {\color{Orchid}\cdot \dfrac{db}{dt}}-{\color{Teal}6(1)} {\color{Orchid}\cdot \dfrac{db}{dt}}+{\color{Teal}2c} {\color{Orchid}\cdot \dfrac{dc}{dt}} ,\phantom{x}{\color{Teal}\text{Power & Constant Multiple Rules}}\text{ , }\color{Orchid}\text{Chain Rule}\\2a\cdot\dfrac{da}{dt} &= (2b -6)\cdot\dfrac{db}{dt}+2c\cdot\dfrac{dc}{dt} \end{aligned}

Substitute the given values for $a$,$b$, $c$, $\dfrac{db}{dt}$, and $\dfrac{dc}{dt}$. Isolate $\dfrac{da}{dt}$ on the left-hand side of the equation to find its value.

\begin{aligned}2a\cdot\dfrac{da}{dt} &= (2b -6)\cdot\dfrac{db}{dt}+2c\cdot\dfrac{dc}{dt}\\2(4)\cdot \dfrac{da}{dt} &=[2(-1) -6]\cdot 4 +2(-2)\cdot3\\8\dfrac{da}{dt} &= -32-12\\8\dfrac{da}{dt}&=-44\\\dfrac{da}{dt}&=-\dfrac{44}{8}\\&=-5.5\end{aligned}

Hence, $\dfrac{da}{dt}$ is equal to $\boldsymbol{-5.5}$.

Example 3

A balloon is being filled with air at the constant rate of $4$ cubic cm per second. How fast is the spherical balloon’s radius increasing when the radius is $6$ cm?  What happens with the radius’ instantaneous rate of change when $r= 12$ cm?

Solution

As we have discussed earlier, the volume and radius of an inflating balloon are increasing as time increases. We can illustrate this to better understand what’s happening as the balloon is filled with air:

Since the balloon’s volume and radius are dependent on time, we can express them as functions of time: $V(t)$ and $r(t)$, respectively.

• Since the volume of air and consequently, the balloon’s volume, is being increased at $4$ cubic cm per second, $\dfrac{dV}{dt}=4$.
• We’re looking for the rate that the radius is increasing, $\dfrac{dr}{dt}$, when $r = 6$ cm.

Recall that the volume of a sphere with a radius of $r$ cm can be expressed as:

\begin{aligned}V&=\dfrac{4}{3}\pi r^3\\V(t) &= \dfrac{4}{3}\pi r(t)^3\end{aligned}

We can use implicit differentiation to find the expression for $\dfrac{dr}{dt}$ in terms of $V$, $r$, and $\dfrac{dV}{dt}$.

\begin{aligned}V&=\dfrac{4}{3}\pi r^3\\\dfrac{d}{dt}(V)&=\dfrac{d}{dt}\left(\dfrac{4}{3}\pi r^3\right)\\ {\color{Teal} (1)}{\color{Orchid}\cdot \dfrac{dV}{dt}} &= {\color{Teal}\dfrac{4}{3}\pi(3r^2)}{\color{Orchid}\cdot \dfrac{dr}{dt}},\phantom{x}{\color{Teal}\text{Constant Multiple & Power Rules}}\text{ , }{\color{Orchid}\text{Chain Rule}}\\\dfrac{dV}{dt} &=4\pi r^2 \dfrac{dr}{dt}\\\dfrac{dr}{dt}&= \dfrac{1}{4\pi r^2}\dfrac{dV}{dt} \end{aligned}

Now that we have the expression for $\dfrac{dr}{dt}$, let’s substitute the values that we already have into the equation.

\begin{aligned}\dfrac{dr}{dt}&= \dfrac{1}{4\pi r^2}\dfrac{dV}{dt}\\&= \dfrac{1}{4\pi(6)^2} \cdot 4\\&= \dfrac{1}{36\pi}\text{ cm/sec} \end{aligned}

This means that the radius is increasing at a rate of $\boldsymbol{\dfrac{1}{36\pi} \text{ cm/sec}}$ when the radius is equal to $6$ cm.

Now, we’ll use the same expression for $\dfrac{dr}{dt}$, $\dfrac{1}{4\pi r^2}\dfrac{dV}{dt}$, but this time, we’ll use $r = 12$ cm.

\begin{aligned}\dfrac{dr}{dt}&= \dfrac{1}{4\pi r^2}\dfrac{dV}{dt}\\&= \dfrac{1}{4\pi(12)^2} \cdot 4\\&= \dfrac{1}{144\pi}\text{ cm/sec} \end{aligned}

This means that the radius’ instantaneous rate of change is $\boldsymbol{\dfrac{1}{144\pi} \text{ cm/sec}}$ when the radius is equal to $12$ cm.

Example 4

Jonathan is observing a plane that is flying directly away from him at $300$ mph at an altitude of $8$ miles. How fast is the plane’s distance (from Jonathan) increasing when the plane is flying over a point on the ground that is $6$ miles from Jonathan?

Solution

Construct a right triangle with Jonathan and the plane’s distance as the triangle’s hypotenuse. The plane is $8$ miles away from the ground, so we can set that as the fixed quantity as shown below.

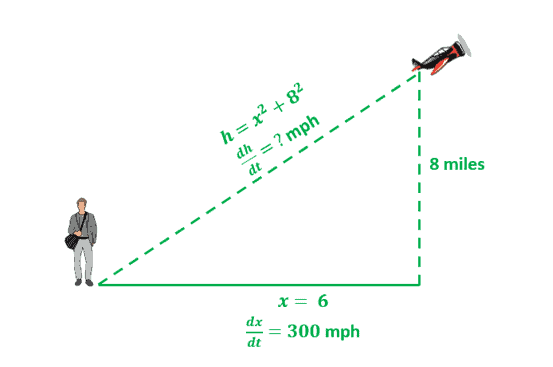
We also know that the plane is flying horizontally away from Jonathan at a speed of $300$ mph, so $\dfrac{dx}{dt}= 300$. We can relate $8$ miles, $x$, and $h$ using the Pythagorean theorem. Let’s also determine the value of $h$ when $x = 6$.

\begin{aligned}h^2 = x^2 + 8^2\\h^2 &= (6)^2 + 64\\h^2 &= 100\\h &=10\end{aligned}

Hence, $h = 10$ miles when $x = 6$ miles. Since both $h$ and $x$ are functions of time, $t$, we can differentiate both sides of the equation with respect to time.

\begin{aligned}\dfrac{d}{dt}(h^2 )&= \dfrac{d}{dt}(x^2 + 8^2)\\\dfrac{d}{dt} (h^2 )&={\color{Teal}\dfrac{d}{dt}(x^2) + \dfrac{d}{dt}(8^2)},\phantom{x}{\color{Teal}\text{Sum Rule}}\\ {\color{Teal}2h}{\color{Orchid}\cdot \dfrac{dh}{dt}}&= {\color{Teal}2x} {\color{Orchid}\cdot \dfrac{dx}{dt}} +{\color{Teal}0},\phantom{x}{\color{Teal}\text{Power & Constant Rules}}\text{ , }{\color{Orchid} \text{Chain Rule}}\\2h\dfrac{dh}{dt}&= 2x\dfrac{dx}{dt}\end{aligned}

 Through implicit differentiation, we have $2h\dfrac{dh}{dt}= 2x\dfrac{dx}{dt}$. Divide both sides of the equation by $2h$ to isolate $\dfrac{dh}{dt}$. Substitute the values, $x = 6$ and $h = 10$, to find the corresponding value of $\dfrac{dh}{dt}$.

\begin{aligned}\dfrac{dh}{dt}&= \dfrac{2x}{2h}\dfrac{dx}{dt}\\&=\dfrac{x}{h}\dfrac{dx}{dt}\\&= \dfrac{6}{10}(300)\\&=180\end{aligned}

This means that the Jonathan and the plane’s distance is increasing at $\boldsymbol{180\text{ mph}}$ when Jonathan is $6$ miles away from the reference point.

Example 5

A cylindrical container that is filled with water has a $4$-foot radius and $10$-foot height. The container is drained so that the water level or depth inside it is decreasing at a rate of $0.2$ feet per second. How fast is the water draining from the cylindrical container?

Solution

Here’s an illustration showing a cylindrical container that is draining its water at a rate of $0.2$ feet per second.

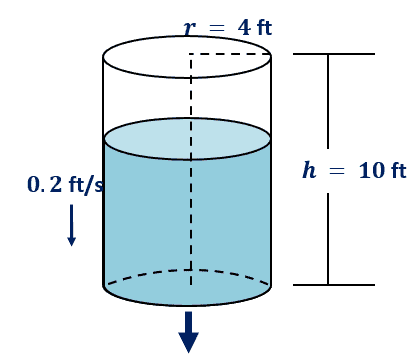
As the depth is reducing at this rate, we can also observe how fast the volume is decreasing over time. We can express the depth and volumes’ rates as $\dfrac{dh}{dt}$ and $\dfrac{dV}{dt}$. Let’s take note of the values that we know so far as well:

• $r = 4$ ft and $h =10$ ft
• $\dfrac{dh}{dt} = -0.2$ ft/s (since depth is decreasing)

Initially, the volume of the water will the same as that of the cylinder’s volume since we know that the container was filled with water at the start. Let’s use the formula for cylinder to relate $V$, $r$, and $h$.

\begin{aligned}V &= \pi r^2 h\end{aligned}

Let’s use implicit differentiate to find how $\dfrac{dV}{dt}$ and $\dfrac{dh}{dt}$ are related based from the equation shown above.

\begin{aligned}\dfrac{d}{dt}(V )&= \dfrac{d}{dt}(\pi r^2 h)\\ {\color{Teal}(1)}{\color{Orchid}\cdot \dfrac{dV}{dt}}&= {\color{Teal}(\pi h)(2r)}{\color{Orchid}\cdot \dfrac{dr}{dt}},\phantom{x}{\color{Teal}\text{Constant Multiple & Power Rules}}\text{ , }{\color{Orchid}\text{Chain Rule}}\\\dfrac{dV}{dt}&= 2\pi rh\dfrac{dr}{dt}\end{aligned}

To find fast the water decreases over time, let’s substitute $r = 4$ ft, $h = 10$ft, and $\dfrac{dh}{dt} = -0.2$ ft/s, into the resulting equation.

\begin{aligned}\dfrac{dV}{dt}&= 2\pi(4)(10)(-0.2)\\&=-16 \pi\end{aligned}

This means that the water inside the cylindrical container is decreasing by $\boldsymbol{-16\pi}$ cubic foot  per second.

Example 6

Alex is observing a particle’s motion based on the $xy$-graph that she’s studying. She has observed that the particle is moving clockwise around a circle that has a radius of $6$ cm and is centered at the origin.  As the particle passes through the point, $(6, 8)$, its horizontal position is changing at a rate of $1.5$ cm per second. How fast is its vertical position changing at that instant?

Solution

Let’s roughly sketch the particle’s motion on an $xy$-coordinate system. Keep in mind that the initial position is already given and so is the rate of the $x$-coordinate’s position, $\dfrac{dx}{dt} = 1.5$ cm per second.

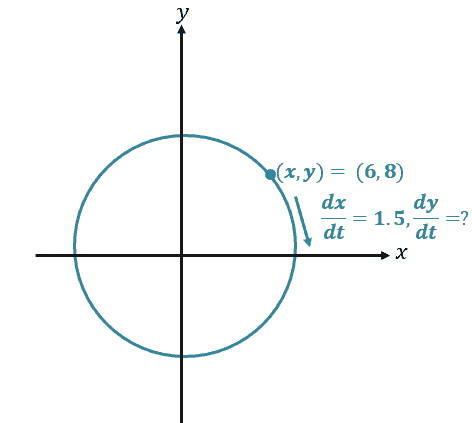
Recall that the equation of a circle centered at the origin is $x^2 + y^2 = r^2$, where $r$ represents the radius of the circle. The radius’ measure can be determined by finding the distance between $(0, 0)$ and $(6, 8)$.

\begin{aligned}d &= \sqrt{(y_2 -y_1)^2 + (x_2 -x_1)^2}\\r&= \sqrt{8^2 + 6^2}\\&= \sqrt{64 +36}\\&= 10\end{aligned}

This means that the particle’s circular path has a radius of $10$ cm.

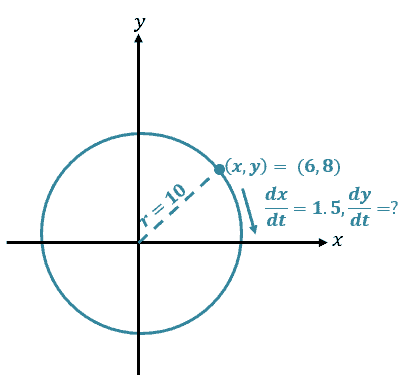
This means that the particle’s circular path has a radius of $10$ cm. Going back to our equation for the circle, we now have $x^2 +y^2 =100$. Let’s take the derivative of both sides of the equation with respect to time, $t$.

\begin{aligned}x^2 + y^2 = r^2\\\dfrac{d}{dt}(x^2 + y^2) &= \dfrac{d}{dt}(r^2)\\ {\color{Teal}\dfrac{d}{dt}x^2 + \dfrac{d}{dt}y^2 }&= {\color{Orchid}0},\phantom{x}{\color{Teal}\text{Sum Rule}}\text{ & }{\color{Orchid}\text{Constant Rule}}\\ {\color{Teal}(2x)}{\color{Orchid}\cdot \dfrac{dx}{dt}}+{\color{Teal}(2y)}{\color{Orchid}\cdot \dfrac{dy}{dt}}&= 0,\phantom{x}{\color{Teal}\text{Power Rule}}\text{ & }{\color{Orchid}\text{Chain Rule}}\\2x \dfrac{dx}{dt}+2y \dfrac{dy}{dt} &=0 \end{aligned}

Let’s substitute the values that we know so far then isolate $\dfrac{dy}{dt}$ to finds its value.

\begin{aligned}2(6)(1.5)+2(8) \dfrac{dy}{dt} &=0\\18 + 16\dfrac{dy}{dt}&= 0\\\dfrac{dy}{dt}&=-\dfrac{18}{16}\\&=-\dfrac{9}{8} \end{aligned}

This shows that when the $x$-coordinate is moving at a rate of $1.5$ cm per second, the particle’s vertical position is decreasing at a rate of $\boldsymbol{\dfrac{9}{8}=1.25}$ cm per second.

Example 7

Janice is standing near a lamppost. The lamppost is $20$ ft tall and Janice is $5$ feet tall. When Janice is walking away from the lamppost at $0.25 $ ft per second creates a shadow behind her. At what rate is the length of the shadow increasing when Janice is $10$ ft away from the lamppost?

Solution

Here’s an illustrated guide to help you better understand the problem. This means that we’re working with two right triangles and we’ve labeled the important values as well.

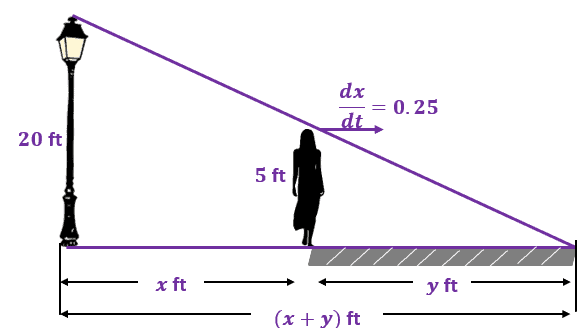
The problem requires us to find the shadow’s length when Janice is $10$ ft away, so we want to find $\dfrac{dy}{dt}$ when $x =10$. These two right triangles are similar triangles. Equate the ratios of the lamppost and Janice’s height to the distance $x=10$ ft and $(x +y)$ ft as shown below.

\begin{aligned}\dfrac{20}{5} &= \dfrac{x + y}{y} \end{aligned}

Simplify the left-hand side of the equation and cross-multiply to simplify the equation further.

\begin{aligned}4 &= \dfrac{x + y}{y}\\4y &=  x + y\\3y &= x\end{aligned}

Apply implicit differentiation to find the relationship between $\dfrac{dx}{dt}$ and $\dfrac{dy}{dt}$.

\begin{aligned}\dfrac{d}{dt}(3y )&=\dfrac{d}{dt} (x)\\ {\color{Teal}3(1)}{\color{Orchid} \cdot\dfrac{dy}{dt}}&= {\color{Teal}(1)}{\color{Orchid} \cdot\dfrac{dx}{dt}},\phantom{x}{\color{Teal} \text{Constant Multiple & Power Rules}},{\color{Orchid}\text{Chain Rule}}\\3\dfrac{dy}{dt} &= \dfrac{dx}{dt}\end{aligned}

Substitute $\dfrac{dx}{dt}$ with $0.25$ then divide both sides by $3$ to find $\dfrac{dy}{dt}$.

\begin{aligned}3\dfrac{dy}{dt} &= 0.25\\\dfrac{dy}{dt}&= \dfrac{0.25}{3}\\&=\dfrac{1}{4} \cdot \dfrac{1}{3}\\&=\dfrac{1}{12}\end{aligned}

This means that the shadow’s length is increasing by $\boldsymbol{1}{12}$ ft/sec.

Practice Questions

1. Charlie is monitoring the volume, in cubic feet, measured inside the balloon. The volume is measured after $t$ minutes of expansion and $V’(t)$ models the volume’s behavior. Which of the following must be the units used to measure $V’(t)$?
a. Cubic
b. Feet
c. Cubic per minute
d. Cubic feet per minute
2. Given that, $a$, $b$, and $c$ satisfy the equation, $a^2 = b^2+ 4b + c^2$, find $\dfrac{da}{dt}$, if we have the following values:
• $a=1$,$b = -2$ and $c = -1$
• $\dfrac{db}{dt} = 6$ and $\dfrac{dc}{dt} = 2$
3. A spherical balloon is being filled with air at the constant rate of $8$ cubic cm per second. How fast is the spherical balloon’s radius increasing when the radius is $2$ cm? What happens with the radius’ instantaneous rate of change when $r= 4$ cm?
4. Marielle is observing a plane that is flying directly away from her at $260$ mph at an altitude of $12$ miles. How fast is the plane’s distance (from Marielle) increasing when the plane is flying over a point on the ground that is $5$ miles from her?
5. A cylindrical container that is filled with water has an $8$-foot radius and $20$-foot height. The container is drained so that the water level or depth inside it is decreasing at a rate of $0.1$ feet per second. How fast is the water draining from the cylindrical container?
6. James is observing a particle’s motion based on the $xy$-graph that he’s studying. He has observed that the particle is moving clockwise around a circle that has a radius of $6$ cm and is centered at the origin. As the particle passes through the point, $(5, 12)$, its horizontal position is changing at a rate of $2$ cm per second. How fast is its vertical position changing at that instant?
7. Harold is standing near a lamppost. The lamppost is $40$ ft tall and Harold is $5$ feet tall. When Harold is walking away from the lamppost at $2.10$ ft per second creates a shadow behind him. At what rate is the length of the shadow increasing when Harold is $15$ ft away from the lamppost?

Answer Key

1. d. Cubic feet per minute
2. $\dfrac{da}{dt}= -2$
3.
• $\dfrac{dr}{dt}= \dfrac{1}{2\pi} \text{ cm/sec}$
• $\dfrac{dr}{dt}= \dfrac{1}{8\pi} \text{ cm/sec}$
4. $100\text{ mph}$
5. $32$ cubic foot
6. $\dfrac{dy}{dt} = – \dfrac{5}{6}$ or decreasing at a rate of $\dfrac{5}{6}$ cm/sec
7. $0.30$ ft/s