Implicit differentiation – Definition, Process, and Examples

Implicit differentiation allows us to differentiate expressions (usually within an equation) that contain two or more variables. In our discussion, we will focus on implicitly differentiating equations with two variables. This technique is in fact an extension of the chain rule and you’ll learn why in our discussion.

Implicit differentiation is an important differential calculus technique that allows us to determine the derivative of $\boldsymbol{y}$ with respect to $\boldsymbol{x}$ without isolating $\boldsymbol{y}$ first.

In this article, we’ll focus on differentiating equations written implicitly. To make the most out of the discussion, refresh your notes on the following:

• The fundamental derivative rules that we’ve learned in the past.
• This also includes reviewing your knowledge of trigonometric derivatives, exponential derivatives, and the derivative of $\ln x$.
• The implicit differentiation is an extension of the chain rule, so review your notes on this topic too.

Are you ready? Let’s begin by understanding the difference between implicit and explicit functions. By the end of this discussion and series of exercises, differentiating equations of circles will be second nature to you!

What is implicit differentiation?

Implicit differentiation will help us differentiate equations that contain both $\boldsymbol{x}$ and $\boldsymbol{y}$. This technique allows us to determine the slopes of tangent lines passing through curves that are not considered functions. Circles are great examples of curves that will benefit from implicit differentiation.

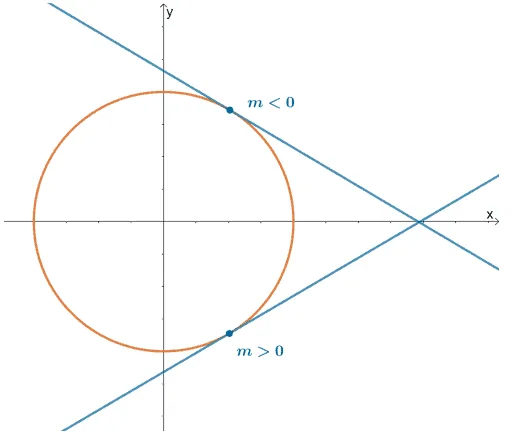
Here’s a graph of a circle with two tangent lines passing through the curve. From this, we can see that the sign of the slope’s tangents will vary depending on the point’s position. Through implicit differentiation, we’ll be able to find the general rules for these slopes despite the fact that the circle is not a function.

To understand which functions would benefit from this technique, let’s briefly review the difference between explicit and implicit equations or functions.

• Explicit functions are simply the functions written in terms of the independent variable. They are normally of the form, $y = f(x)$.
• Implicit functions, on the other hand, are written in terms of both the independent and dependent variables.

Here are examples of equations that are known to be explicit and implicit functions.

Recall that $\dfrac{dy}{dx}$ refers to differentiating $y$ in terms of $x$. We can determine $\dfrac{dy}{dx}$ for these implicit equations by differentiating $g(x, y) = 0$ and accounting for $\dfrac{dy}{dx}$ in the terms containing $y$ as variables.

Revising the chain rule for the implicit differentiation formula

Implicit differentiation will not be possible without the chain rule.

Implicit differentiation will not be possible without the chain rule. That’s because the chain rule allows us to differentiate composite functions. In implicit functions or equations, we will treat $y$ as if it’s a composite function (with $x$ embedded within the function).

Let’s say we want to differentiate the implicit equation, $g(x,y) = 0$, we can account for $\dfrac{dy}{dx}$ from terms containing either $x$ or $y$. 

• When working with the terms with $x$, we simply apply the derivative rules in the past immediately.
• The terms containing $y$ as variables, $f(y)$ for example, will have to account for both $\dfrac{d}{dy} f(y)$ and $\dfrac{dy}{dx}$. This is only possible through chain rule.

\begin{aligned} \dfrac{d}{dx} f(y) = \dfrac{d}{dy} f(y) \cdot \dfrac{dy}{dx}\end{aligned}

Through this technique, we’ll eventually be able to isolate $\boldsymbol{\dfrac{dy}{dx}}$ and have an implicit differentiation in terms of $\boldsymbol{x}$ and $\boldsymbol{y}$.

How to do implicit differentiation?                

Now that we understand the definition of implication differentiation, its importance, as well as its origin, it’s time that we learn how to apply these when differentiating implicit equations.

Implicit differentiation steps

When given an implicit equation, use the steps shown below to find the expression for $\dfrac{dy}{dx}$ in terms of $x$ and $y$:

• Take the derivative of both sides of the equation. Remember that $y$ is still a function of $x$.
• Apply the chain rule whenever needed – for composite functions in terms of $x$ and functions in terms of $y$.
• Use algebraic manipulation to isolate $\dfrac{dy}{dx}$ on the left-hand side of the equation.

The best way to master this technique is through practice, so let’s begin using these steps to find $\dfrac{dy}{dx}$ for the implicit equation, $x^2 + y^2  = 16$.

We can first take the derivative of both sides of the equation of the circle. Use the fundamental derivative rules to simplify the left-hand side of the equation.

\begin{aligned}\dfrac{d}{dx} (x^2 + y^2) &= \dfrac{d}{dx} 16\\ {\color{Teal}\dfrac{d}{dx}x^2 + \dfrac{d}{dx}y^2} &= {\color{DarkOrange}0},\phantom{x}{\color{Teal}\text{Sum Rule}}\text{ & }{\color{DarkOrange}\text{Constant Rule}}\end{aligned}

When differentiating $y^2$, make sure to account for $\dfrac{dy}{dx}$ through the chain rule.

\begin{aligned}\dfrac{d}{dx} (x^2 + y^2) &= \dfrac{d}{dx} 16\\ {\color{Teal}\dfrac{d}{dx}x^2 + \dfrac{d}{dx}y^2} &= {\color{DarkOrange}0},\phantom{x}{\color{Teal}\text{Sum Rule}}\text{ & }{\color{DarkOrange}\text{Constant Rule}}\\ {\color{Teal}2x} + {\color{Teal}2y} \cdot {\color{DarkOrange}\dfrac{dy}{dx}} &=0\phantom{x}{\color{Teal}\text{Power Rule}}\text{ & }{\color{DarkOrange}\text{Chain Rule}}\\2x+2y\cdot\dfrac{dy}{dx}&=0\end{aligned}

Isolate $\dfrac{dy}{dx}$ on the left-hand side of the equation by:

• Subtracting $2x$ from both sides of the equation.
• Dividing both sides of the resulting equation by $2y$.

\begin{aligned}2y \cdot \dfrac{dy}{dx} &= -2x\\\dfrac{dy}{dx}&= -\dfrac{2x}{2y}\\&=-\dfrac{x}{y} \end{aligned}

This means that the implicit derivative of equation, $x^2 + y^2  = 16$, is simply $-\dfrac{x}{y}$.

Apply similar approaches when working on other implicit equations’ derivatives. Here’s another pro-tip: if you want to shorten your solution, you can use $y’$ instead of $\dfrac{d}{dx}$.

We’ve prepared some more equations for you to work on. When you’re ready to apply this new technique, head over to the next section!

Example 1

Given the implicit equation, $-3xy + y^3 = 2x + 3y$, use implicit differentiation to determine $\dfrac{d}{dx}$.

Solution

We’ll follow similar steps to find the expression for $\dfrac{d}{dx}$ from our given equation.

• Begin by differentiating both sides of the equation.
• Apply the derivative rules that you’ve learned in the past to simplify both sides of the equation.
• Make sure to account for $\dfrac{dy}{dx}$ when differentiating terms containing $y$.

\begin{aligned}\dfrac{d}{dx}(-3xy + y^3) &= \dfrac{d}{dx}(2x + 3y)\\\dfrac{d}{dx} (-3xy) + \dfrac{d}{dx}y^3 &= \dfrac{d}{dx}2x + \dfrac{d}{dx}3y,\phantom{x}{\color{Teal}\text{Sum Rule}}\\ {\color{Teal}-3\dfrac{d}{dx} xy }+ \dfrac{d}{dx}y^3 &= {\color{Teal}2\dfrac{d}{dx}x} + {\color{Teal}3\dfrac{d}{dx}y},\phantom{x}{\color{Teal}\text{Constant Multiple Rule}}\\-3\dfrac{d}{dx}xy + {\color{Teal}3y^2}{\color{DarkOrange}\dfrac{dy}{dx}} &= 2({\color{Teal}1})+ 3({\color{Teal}1}) {\color{DarkOrange}\dfrac{dy}{dx}},\phantom{x}{\color{Teal}\text{Power Rule}}\text{ & } {\color{DarkOrange}\text{Chain Rule}}\\-3\left({\color{Teal} x \dfrac{d}{dx}y + y\dfrac{d}{dx}x }\right) + 3y^2 \dfrac{dy}{dx}&= 2 + 3\dfrac{dy}{dx},\phantom{x}{\color{Teal}\text{Product Rule}}\end{aligned}

Simply the left-hand side of the equation further by applying the power rule.

\begin{aligned}-3\left(x \dfrac{d}{dx}y + y\dfrac{d}{dx}x\right) + 3y^2 \dfrac{dy}{dx}&= 2 + 3\dfrac{dy}{dx}\\ -3\left[x{\color{Teal}  (1)}{\color{DarkOrange}\dfrac{dy}{dx}}+ y{\color{Teal}(1)}\right] + 3y^2 \dfrac{dy}{dx}&= 2 + 3\dfrac{dy}{dx},\phantom{x}{\color{Teal}\text{Power Rule}}\text{ & }{\color{DarkOrange}\text{Chain Rule}}\\-3x\dfrac{dy}{dx}-3y + 3y^2 \dfrac{dy}{dx}&= 2 + 3\dfrac{dy}{dx}\end{aligned}

Rearrange the terms of the equation and isolate all terms containing $\dfrac{dy}{dx}$ on the left-hand side of the equation.

\begin{aligned}-3x\dfrac{dy}{dx}-3y + 3y^2 \dfrac{dy}{dx}&= 2 + 3\dfrac{dy}{dx}\\-3x\dfrac{dy}{dx}+ 3y^2 \dfrac{dy}{dx}-3\dfrac{dy}{dx}&= 2+3y\\-3\dfrac{dy}{dx}(x-y^2 +1)&= 2 + 3y  \end{aligned}

Divide both sides of the equation by $-3(x-y^2+1)$ to find the expression for $\dfrac{dy}{dx}$.

\begin{aligned}\dfrac{-3\dfrac{dy}{dx}(x-y^2 +1)}{-3(x-y^2 +1)}&= \dfrac{2 + 3y}{-3(x-y^2 +1)}\\\dfrac{dy}{dx}&= -\dfrac{2x+ 3y}{x-y^2 +1}  \end{aligned}

This shows that we have $\dfrac{dy}{dx} = -\dfrac{2x + 3y}{x –y^2 +1}$ through implicit differentiation.

Example 2

Given the implicit equation, $y^2 +6y+9 = 4x$, use implicit differentiation to determine the following:

a. Expression for $y’$.
b. Slopes of the tangent lines passing through the equation’s curve and the points, $(4, -7)$ and $(4, 1)$.
c. Graph the curve of the equation and the tangent lines passing through the given points.

.Solution

Let’s focus of finding the expression for $y’$ or $\dfrac{dy}{dx}$. Take the derivative of both sides of the equation then apply fundamental derivative rules to simplify both sides of the equation.

\begin{aligned}\dfrac{d}{dx}(y^2 +6y+9 )= \dfrac{d}{dx}(4x)\\ {\color{Teal}\dfrac{d}{dx}y^2 +\dfrac{d}{dx}6y+\dfrac{d}{dx}9 } &= \dfrac{d}{dx}(4x),\phantom{x}{\color{Teal}\text{Sum Rule}}\\ \dfrac{d}{dx}y^2 + {\color{DarkOrange}6\dfrac{d}{dx}y} + {\color{Teal}0} &={\color{DarkOrange} 4\dfrac{d}{dx}x},\phantom{x}{\color{Teal}\text{Constant Rule}}\text{ & }{\color{DarkOrange}\text{Constant Multiple Rule}}\\\dfrac{d}{dx}y^2 + 6\dfrac{d}{dx}y &= 4\dfrac{d}{dx}x\end{aligned}

Simplify both sides of the equation by using the power rule. Account for $\dfrac{dy}{dx}$ in the terms found at the left-hand side through chain rule.

\begin{aligned}{\color{Teal}(2y)} \cdot {\color{DarkOrange}\dfrac{dy}{dx} }+ 6{\color{Teal}(1)} \cdot {\color{DarkOrange}\dfrac{dy}{dx} } &= 4{\color{Teal}(1)},\phantom{x}{\color{Teal}\text{Power Rule}} \text{ & }{\color{DarkOrange}\text{Chain Rule}}\\(2y + 6)\dfrac{dy}{dx}&= 4 \end{aligned}

After factoring out $\dfrac{dy}{dx}$, divide both sides of the equation by $(2y +6)$ to isolate $\dfrac{dy}{dx}$ on the left-hand side of the equation.

\begin{aligned}\dfrac{(2y + 6)\dfrac{dy}{dx}}{(2y + 1)}&= \dfrac{4}{(2y + 6)}\\\dfrac{dy}{dx} &= \dfrac{4}{2y +6}\\&=\dfrac{4}{2(y + 3)}\\&= \dfrac{2}{y+3} \end{aligned}

a. This shows that $\dfrac{d}{dx} = y’ = \dfrac{2}{y+3}$.

Now that we have the expression for $y’$, we can use each of the two given points, $(4, -7)$ and $(4, 1)$, to find two slopes of the tangent lines passing through the equation’s curve. Recall that $y’$ will represent the tangent line’s slope passing through the given points.

b. From this, we can see that the curve has tangent lines with slopes, $-\dfrac{1}{2}$ and $\dfrac{1}{2}$.

The equation, $y^2 +6y+9 = 4x$, can be written as $(y + 3)^2  = 4x$. When studying about conic sections, we know that this equation represents a parabola centered at $(0, -3)$ and opens to the right.

Let’s include the graph of the tangent line with slopes, $m = -\dfrac{1}{2}$ and $m = \dfrac{1}{2}$. Make sure that the tangent lines pass through the points, $(4, -7)$ and $(4, 1)$, respectively.

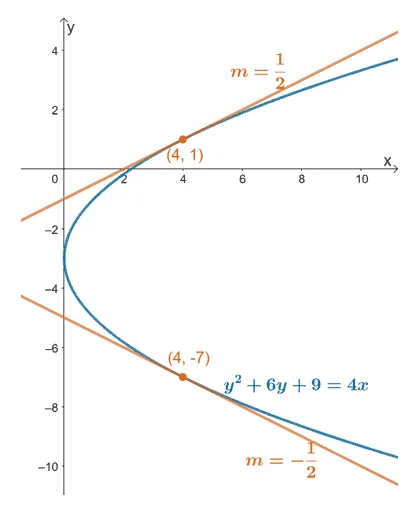
c. This graph shows the sketch of the curve (which clearly is not a function) along with the two tangent lines we’ve derived through implicit differentiation.

Practice Questions

1. Given the implicit equations shown below, use implicit differentiation to determine $\dfrac{d}{dx}$.
a. $4x^2 – 3y^3 = -8x + y^2$
b. $2x^3 + 6x^2y = 6x^3$
c. $x\sqrt{y – 4} = 2xy + 3$
2. Given the implicit equations shown below, use implicit differentiation to determine $\dfrac{d}{dx}$.
a. $x^2 + y^3 – x^3 + 8 = 12$
b. $e^{xy} = y -x$
c. $ 6x^4+\tan y=3y^2-4x$
3. Given the implicit equation, $4x^2-9y^2 = 36$, use implicit differentiation to determine the following:
a. Expression for $y’$.
b. Slopes of the tangent lines passing through the equation’s curve and the points, $\left(-5, \dfrac{8}{3}\right)$ and $\left(5, \dfrac{8}{3}\right)$.
c. Graph the curve of the equation and the tangent lines passing through the given points.

Answer Key

1.
a. $\dfrac{dy}{dx} = \dfrac{8 +8x}{y\left(2 + 9y\right)}$
b. $\dfrac{dy}{dx} = \dfrac{2\left(x -y\right)}{x}$
c. $\dfrac{dy}{dx} = \dfrac{8 – 2y}{x}$
2.
a. $\dfrac{d}{dx} = \dfrac{3x^2-2x}{3y^2}$
b. $\dfrac{d}{dx} = \dfrac{-1-e^{xy}y}{e^{xy}x-1}$
c. $\dfrac{d}{dx} = \dfrac{-4-24x^3}{\sec ^2\left(y\right)-6y}$
3.
a. $y’ = \dfrac{4x}{9y}$
b. $m =\pm \dfrac{5}{6}$
c.

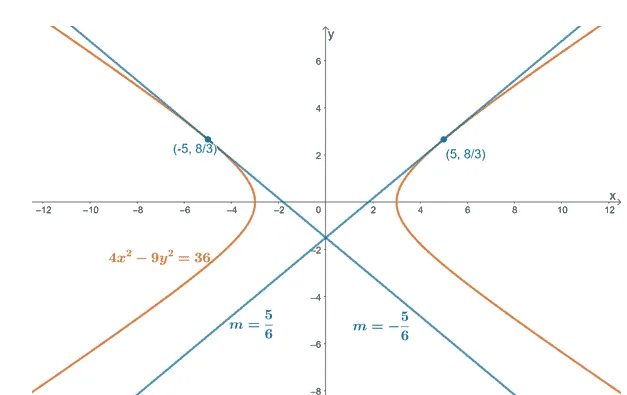
Images/mathematical drawings are created with GeoGebra.