- Home
- >
- Exponential derivative – Derivation, Explanation, and Example
JUMP TO TOPIC
Exponential derivative – Derivation, Explanation, and Example
In differential calculus, we’ll need to also establish a rule for exponential derivative. Our discussion will revolve around the formula for $\dfrac{d}{dx} a^x$ and $\dfrac{d}{dx} e^x$. Exponential functions have a wide range of applications in different STEM fields, so it’s essential to understand how its derivative behaves.
The derivative of an exponential function will be the function itself and a constant factor. A special case occurs for $\boldsymbol{e^x}$ since the derivative is $\boldsymbol{e^x}$ as well.
In this article, we’ll understand how we could come up with the exponential functions’ derivative rules. We’ll also see how we can apply them to differentiate a wide range of functions. This is why it’s important to take a refresher on the following topics:
- Review how we derive derivative rules from the formal definition of derivatives.
- Understand the components of an exponential function.
- Apply the fundamental derivative rules with these new derivative rules.
Let’s begin by understanding the factors that we can find in the exponential function’s derivative. We’ll eventually learn how to apply this rule to solve problems involving exponential functions.
What is the derivative of an exponential function?
Recall that an exponential function has a general form of $y = a^x$, where $a > 0$ but $a \neq 1$. We call $a$ the base, and $x$ is in the exponent part of the expression. For functions like this, the derivative will be the function itself times the base’s natural logarithm.
\begin{aligned}\dfrac{d}{dx} a^x &= a^x \ln a\end{aligned}
Let’s go ahead and observe how an exponential function and its derivative would look like when graphed on an $xy$-plane.
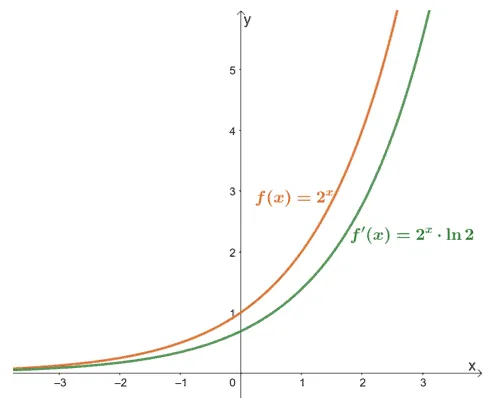
The graph of $f(x) = 2^x$ and $f’(x) = 2^x \cdot \ln2$ confirm the fact that the derivative of an exponential function is an exponential function itself. The only difference is that the derivative will have a constant factor.
There’s a special case for the exponential derivative rules, which occurs when $a = e$. Recall that $\ln e = 1$, so we can use this logarithmic property to simplify the formula for $\dfrac{d}{dx} e^x$ as shown below.
\begin{aligned}\dfrac{d}{dx} e^x &= e^x\ln e\\&= e^x \cdot 1\\&= e^x\end{aligned}
These two derivative rules will also apply to composite functions. We have to account for the inner function’s derivative through chain rule.
Here’s a table summarizing the derivative rules for exponential functions:
Derivative Rules Base of $\boldsymbol{a}$ | Derivative Rules Base of $\boldsymbol{e}$ |
| \begin{aligned}\dfrac{d}{dx} a^x &= a^x \ln a\end{aligned} | \begin{aligned}\dfrac{d}{dx} e^x &= e^x\end{aligned} |
| \begin{aligned}\dfrac{d}{dx} a^{[g(x)]} &= a^{[g(x)]} \ln [g(x)] \cdot g’(x)\end{aligned} | \begin{aligned}\dfrac{d}{dx} e^{[g(x)]} &= e^{[g(x)]} \cdot g’(x)\end{aligned} |
Keep these four variations in mind when working on the sample problems we’ve provided. For now, let’s understand the reason behind these derivative rules by differentiating $a^x$ using the formal definition of derivatives. We’ll eventually learn how to apply this rule to solve problems involving exponential functions.
Proof of the derivative rule for exponential functions
Recall that $\dfrac{d}{dx} f(x) = \lim_{h\rightarrow 0}\dfrac{f(x + h) – f(x)}{h}$, so we can use this to confirm the derivative that we’ve just learned for $y = a^x$.
- Use the product rule for exponents,$a^{m} \cdot a^n = a^{m+n}$, to factor $a^x$ from the numerator.
- Since $a^x$ is considered a constant for this expression, we can factor it out of $\lim_{h \rightarrow 0}$.
- Evaluate the limit by setting $h$ to $0$.
\begin{aligned}y’ &= \lim_{h\rightarrow 0} \dfrac{a^{x + h} – a^x}{h}\\&= \lim_{h\rightarrow 0} \dfrac{a^x(a^h – 1)}{h}\\&= a^x\lim_{h\rightarrow 0}\dfrac{a^h – 1}{h}\end{aligned}
The limit of exponential functions of the form $\dfrac{a^h – 1}{h}$ as $h \rightarrow 0$ is said to be $\ln a$, so we’ll use this property to rewrite $y’$.
\begin{aligned}y’ &=a^x \ln a\end{aligned}
This confirms the exponential derivative rule – $\dfrac{d}{dx} a^x = a^x \ln a$.
How to find the derivative of an exponential function?
The most important step in differentiating exponential functions is to make sure that we’re actually working with exponential functions. Make sure that the function has a constant base and $\boldsymbol{x}$ is found at the exponent.
Once we’ve confirmed that the function (or the composite function’s outer layer) has a form of either $y= a^x$ or $y = e^x$, we can then apply the derivative rule we’ve just learned.
- To find the function’s derivative, copy the original function.
- Multiply this with the natural logarithm of the base. (Skip this when working with $y= e^x$.)
- If working with composite functions, multiply the result with the derivative of the inner function.
We’ll show you four examples in which the derivative rule for exponential functions were applied. We’ll include the other rules used whenever possible.
| \begin{aligned}\boldsymbol{\dfrac{d}{dx} a^x = a^x \ln a}\end{aligned} | \begin{aligned}\boldsymbol{\dfrac{d}{dx} e^x = e^x}\end{aligned} |
| \begin{aligned}\dfrac{d}{dx} (5^x) &= 5^x \cdot \ln 5,\phantom{x}\color{DarkOrange}\text{Derivative of }a^x \end{aligned} | \begin{aligned}\dfrac{d}{dx} (6e^x) &= 6\cdot \dfrac{d}{dx}e^x,\phantom{x}\color{DarkOrange}\text{Constant Multiple Rule}\\&= 6\cdot{\color{DarkOrange}e^x},\phantom{x}\color{DarkOrange}\text{Derivative of }e^x \\&= 6e^x\end{aligned} |
| \begin{aligned}\dfrac{d}{dx} (2^{3x}) &= {\color{DarkOrange}2^{3x} \cdot \ln 2}\cdot {\color{Green}\dfrac{d}{dx} 3x},\phantom{x}{\color{DarkOrange}\text{Derivative of }a^x}\text{ & }\color{Green}\text{Chain Rule}\\&= (2^{3x}\ln 2)\cdot\left({\color{DarkOrange}3\cdot \dfrac{d}{dx}x} \right ),\phantom{x}\color{DarkOrange}\text{Constant Multiple Rule}\\&= (2^{3x}\ln 2)\cdot3({\color{DarkOrange}1}),\phantom{x}\color{DarkOrange}\text{Power Rule}\\&=(3\ln 2)2^{3x} \end{aligned} | \begin{aligned}\dfrac{d}{dx} (e^{5x}) &= {\color{DarkOrange}e^{5x}}\cdot {\color{Green}\dfrac{d}{dx} 5x},\phantom{x}{\color{DarkOrange}\text{Derivative of }e^x}\text{ & }\color{Green}\text{Chain Rule}\\&= (e^{5x})\cdot\left({\color{DarkOrange}5\cdot \dfrac{d}{dx}x} \right ),\phantom{x}\color{DarkOrange}\text{Constant Multiple Rule}\\&= (e^{5x})\cdot5({\color{DarkOrange}1}),\phantom{x}\color{DarkOrange}\text{Power Rule}\\&=5e^{5x} \end{aligned} |
These four examples show us how functions and composite functions can be differentiated using the exponential functions’ derivative rules. Review these four functions and when you’re ready, try out the practice problems below!
Example 1
Find the derivative of the following exponential functions.
a. $f(x) = 3^{4x}$
b. $g(x) = 2^x – 6^x$
c. $h(x) = 5^x + e^x – 4^x$
Solution
For $f(x)$, we can apply the derivative rule for exponential function and the chain rule to differentiate it.
\begin{aligned}\dfrac{d}{dx} (3^{4x}) &= {\color{DarkOrange}3^{4x} \cdot \ln 3}\cdot {\color{Green}\dfrac{d}{dx} 4x},\phantom{x}{\color{DarkOrange}\text{Derivative of }a^x}\text{ & }\color{Green}\text{Chain Rule}\\&= (3^{4x}\ln 3)\cdot\left({\color{DarkOrange}4\cdot \dfrac{d}{dx}x} \right ),\phantom{x}\color{DarkOrange}\text{Constant Multiple Rule}\\&= (3^{4x}\ln 3)\cdot4({\color{DarkOrange}1}),\phantom{x}\color{DarkOrange}\text{Power Rule}\\&=(4\ln 3)3^{4x} \end{aligned}
The second function is straightforward. We’ll have to apply the difference rule and the exponential function’s derivative rule to determine $g’(x)$.
\begin{aligned}\dfrac{d}{dx} (2^x – 6^x) &= \dfrac{d}{dx} 2^x – \dfrac{d}{dx} 6^x,\phantom{x}\color{DarkOrange}\text{Difference Rule}\\&= {\color{DarkOrange}(2^x\ln 2)} – {\color{DarkOrange}(6^x\ln 6)},\phantom{x}\color{DarkOrange}\text{Derivative of }a^x\end{aligned}
Hence, we have $g’(x) = (2^x\ln 2) – 6^x\ln 6$.
We’ll apply a similar process for $h(x)$ as shown below.
\begin{aligned}\dfrac{d}{dx} (5^x +e^x -4^x) &= \dfrac{d}{dx} 5^x+ \dfrac{d}{dx} e^x – \dfrac{d}{dx}4^x,\phantom{x}\color{DarkOrange}\text{Sum & Difference Rules}\\&= \dfrac{d}{dx} 5^x- \dfrac{d}{dx}4^x+ \dfrac{d}{dx} e^x \\&= {\color{DarkOrange}(5^x \ln 5 -4^x \ln 4)} + {\color{Green}e^x},\phantom{x}{\color{DarkOrange}\text{Derivative of }a^x}\text{ & }\color{Green}\text{Derivative of }e^x\\&= 5^x \ln 5 -4^x \ln 4 +e^x \end{aligned}
This shows that $h’(x) = 5^x \ln 5 -4^x \ln 4 +e^x$.
Example 2
Find the derivative of the following exponential functions.
a. $f(x) = 2^{4x + 2}$
b. $g(x) = 3^{3x^2 – 4}$
c. $h(x) = e^{6^x}$
Solution
These three sets of functions are composite functions with $y = 2^x$, $y = 3^x$, and $y = e^x$, respectively. We’ll have to differentiate the inner functions for each item through chain rule. Let’s begin with $f(x) = 2^{4x + 2}$.
\begin{aligned}\dfrac{d}{dx} (2^{4x + 2}) &= {\color{DarkOrange}2^{4x + 2} \cdot \ln 2}\cdot {\color{Green}\dfrac{d}{dx} (4x + 2)},\phantom{x}{\color{DarkOrange}\text{Derivative of }a^x}\text{ & }\color{Green}\text{Chain Rule}\\&= (2^{4x + 2}\ln 2)\cdot\left({\color{DarkOrange}\dfrac{d}{dx}4x + \dfrac{d}{dx} 2 } \right ),\phantom{x}\color{DarkOrange}\text{Sum Rule}\\&= (2^{4x + 2}\ln 2)\cdot\left({\color{DarkOrange}4\dfrac{d}{dx}x } + {\color{Green}0}\right ),\phantom{x}{\color{DarkOrange}\text{Constant Multiple Rule}}\text{ & }\color{Green}\text{Constant Rule} \\&= (2^{4x + 2}\ln 2)\cdot4({\color{DarkOrange}1}),\phantom{x}\color{DarkOrange}\text{Power Rule}\\&= (4\ln 2)(2^{4x + 2})\end{aligned}
With the help of fundamental derivative rules, we have $f’(x) = (4\ln 2)(2^{4x + 2})$.We’ll apply a similar process to differentiate $g(x)$.
\begin{aligned}\dfrac{d}{dx} (3^{3x^2 – 4}) &= {\color{DarkOrange}3^{3x^2 – 4} \cdot \ln 3}\cdot {\color{Green}\dfrac{d}{dx} (3x^2 – 4)},\phantom{x}{\color{DarkOrange}\text{Derivative of }a^x}\text{ & }\color{Green}\text{Chain Rule}\\&= (3^{3x^2 – 4} \ln 3)\cdot\left({\color{DarkOrange}\dfrac{d}{dx}3x^2 – \dfrac{d}{dx} 4 } \right ),\phantom{x}\color{DarkOrange}\text{Difference Rule}\\&= (3^{3x^2 – 4} \ln 3)\cdot\left({\color{DarkOrange}3\dfrac{d}{dx}x^2 } + {\color{Green}0}\right ),\phantom{x}{\color{DarkOrange}\text{Constant Multiple Rule}}\text{ & }\color{Green}\text{Constant Rule} \\&= (3^{3x^2 – 4} \ln 3)\cdot3({\color{DarkOrange}2x}),\phantom{x}\color{DarkOrange}\text{Power Rule}\\&= (6x\ln 3)(3^{3x^2 – 4} )\end{aligned}
Hence, we have $g’(x) = (6x\ln 3)(3^{3x^2 – 4} )$. Let’s now work on $h(x)$ use the following rules to begin finding $h’(x)$.
- Derivative rule for $e^x$: $\dfrac{d}{dx} e^x = e^x$.
- Apply the chain rule and use $\dfrac{d}{dx} a^x = a^x \ln x$.
\begin{aligned}\dfrac{d}{dx} (e^{6^x}) &= {\color{DarkOrange}e^{6^x}}\cdot {\color{Green}\dfrac{d}{dx} 6^x},\phantom{x}{\color{DarkOrange}\text{Derivative of }e^x}\text{ & }\color{Green}\text{Chain Rule}\\&= (e^{6^x})\cdot\left({\color{DarkOrange}} 6^x \ln 6\right ),\phantom{x}\color{DarkOrange}\text{Derivative of }a^x\\&= (6^x \ln 6)(e^{6x})\end{aligned}
This shows that $h’(x) = (6^x \ln 6)(e^{6x})$.
We’ve been working on differentiating different functions. Why don’t we try using this derivative rule to answer a word problem this time?
Example 3
An organism that is being studied has an initial population of $500$. After $x$ days, the population can be modeled by the function, $p(x)=500e^{0.4x}$. Jack tells his colleagues that they should expect the ratio of $p’(x)$ and $p(x)$ to be a constant. Is Jack correct?
Solution
Use the natural exponential function’s derivative rule and the chain rule to find the expression for $p’(x)$.
\begin{aligned}\dfrac{d}{dx} (500e^{0.4x}) &= 500 \dfrac{d}{dx}e^{0.4x},\phantom{x}\color{DarkOrange}\text{Constant Multiple Rule}\\&= 500({\color{DarkOrange}e^{0.4x}})\cdot {\color{Green}\dfrac{d}{dx} (0.4x)},\phantom{x}{\color{DarkOrange}\text{Derivative of }e^x}\text{ & }\color{Green}\text{Chain Rule}\\&= 500e^{0.4x}\cdot\left({\color{DarkOrange}0.4\dfrac{d}{dx}x } \right ),\phantom{x}\color{DarkOrange}\text{Constant Multiple Rule}\\&= 500e^{0.4x}\cdot (0.4)({\color{DarkOrange}1}),\phantom{x}\color{DarkOrange}\text{Power Rule}\\&=200e^{0.4x}\end{aligned}
Now that we have $p’(x)$, we can check whether $\dfrac{p’(x)}{p(x)}$ is indeed a constant. You can use fundamental derivative rules to further simplify the expression for $p’(x)$.
\begin{aligned} \dfrac{p’(x)}{p(x)} &= \dfrac{200e^{0.4x}}{500e^{0.4x}}\\&= \dfrac{200}{500}\\&= 0.4\end{aligned}
This shows that the ratio of the rate of change of the population and the actual population size is constant, so Jack is correct.
Practice Questions
1. Find the derivative of the following exponential functions.
a. $f(x) = 6^{2x}$
b. $g(x) = 4^x + 5^x$
c. $h(x) = 8^x – 2e^x + 6^x$
2. Find the derivative of the following exponential functions.
a. $f(x) = 8^{3x – 5}$
b. $g(x) = 6^{\sqrt{x – 1}}$
c. $h(x) = 5^{e^x}$
3. An organism that is being studied has an initial population of $800$. After $x$ days, the population can be modeled by the function, $p(x)=800e^{0.6x}$.
a. What is the ratio of $p’(x)$ and $p(x)$?
b. What is the rate of change of $p’(x)$ after $2$ days?
Answer Key
1.
a. $f’(x) = 9^x2^{2x + 1}\ln 6$
b. $g’(x) = 4^x\ln 4 – 5^x \ln 5$
c. $h’(x) = 8^x\ln 8 – 2e^x + 6^x \ln 6$
2.
a. $f’(x) = (3x\ln8)(8^{3x – 5})$
b. $g’(x) = \dfrac{(\ln 6)(6^{\sqrt{x – 1}})}{2\sqrt{x – 1}}$
c. $h’(x) = 5^{e^x}(e^x \ln 5)$
3.
a. $0.60$
b. $480e^{1.2} \approx 1593.67$
Images/mathematical drawings are created with GeoGebra.
