- Home
- >
- Resultant vector – Explanation and Examples
JUMP TO TOPIC
Resultant Vector – Explanation and Examples
 In vector geometry, the resultant vector is defined as:
In vector geometry, the resultant vector is defined as:
“A resultant vector is a combination or, in simpler words, can be defined as the sum of two or more vectors which has its own magnitude and direction.”
In this topic, we will be covering the following concepts:
- What is a resultant vector?
- How to find the resultant vector?
- How to find the resultant of more than three vectors?
- How to draw the resultant vector?
- What is the formula and method for calculating the resultant vector?
- Examples
- Practice questions.
What Is A Resultant Vector?
A resultant vector is a vector that gives the combined effect of all the vectors. When we add two or more vectors, the outcome is the resultant vector.
Let’s explore this concept with a simple, practical example. Suppose there is a beam with two boxes lying on it, as shown in the figure below:
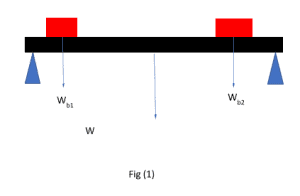
Will you be able to calculate the weight of the beam and the weight of the two boxes? Yes! You can, as you are going to be familiar with the concept of the resultant vector.
In this case, the resultant vector will be the sum of the forces acting on the two boxes, i.e., the boxes’ weight, which will be equal and opposite to the weight of the beam. In this case, the resultant vector will be the sum of two forces as both are parallel and pointing in the same direction.
Suppose there are three vectors in a plane, vector A, B and C. There resultant R can be calculated by adding all three vectors. The resultant R can be determined accurately by drawing a properly scaled and accurate vector addition diagram is shown in the figure below:
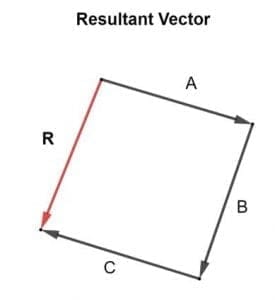
A+B+C = R
Let us have a better understanding of the concept with the help of an example.
Example 1
Calculate the resultant vector of three parallel forces pointing upwards. OA = 5N, OB = 10N and OC = 15N.
Solution
As we know that the resultant vector is given as:
R = OA + OB +OC
R = 5 + 10 + 15
R = 30N
Example 2
Find out the resultant vector of the given vectors OA= (3,4) and OB= (5,7).
Solution
Adding the x-components to find Rx and y-components to calculate RY.
RX=3+5
RX =8
Ry=4+7
Ry =11
So, the resultant vector is R=(8,11)
How To Find The Resultant Vectors
Vectors can be added geometrically by drawing them using a common scale according to the head-to-tail convention, which is defined as
“Join the tail of the first vector with the head of the second vector, which will give another vector whose head is joined with the head of the second vector and tail of the first vector…”
…this is called a resultant vector.
Steps To Find Out The Resultant Vector Using Head-To-Tail Rule
Following are the steps to be followed to add two vectors and find out the resultant vector:
- Draw the first vector according to the selected scale in the given direction.
- Now join the second vector’s tail with the head of the first vector drawn according to the given scale and in the defined direction.
- To draw the resultant vector, join the tail of the first vector with the second vector’s head and put the arrowhead.
- To determine the magnitude, measure the length of resultant R, and to find out the direction, measure the angle of the resultant with the x-axis.
Example 3
Consider a ship sailing at 45o north-east. Then it changes its course in a direction 165o towards the north. Draw the resultant vector.
Solution
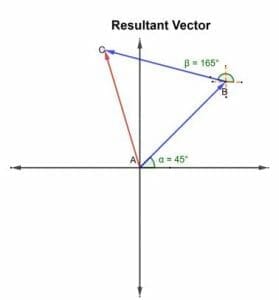
Resultant Vector Of More Than Two Vectors
The rules for finding the resultant of a vector or adding more than two vectors can be protracted to any number of vectors.
R=A+B+C+………………………….
Suppose there are three A, B, and C vectors, as shown in the figures below. To add these vectors, draw them according to the head-to-tail rule such that the head of one vector coincides with the other vector. So, the resultant vector is given as follow:
R=A+B+C
Note: Vector addition is commutative in nature; the sum is independent of the order of addition.
R=A+B+C=C+B+C
Calculating Resultant Vector Using Rectangular Components
Finding a resultant vector using components of a vector is known as an analytical method; this method is more mathematical than geometrical and can be regarded as more accurate and precise than the geometrical method, i.e., configuring using the head-to-tail rule.
Suppose there are two vectors A and B, making angles θA and θB respectively with the positive x-axis. These vectors will be resolved into their components. They will be used to calculate the resultant x and y components of the resultant vector R, which will be the sum of the two vectors’ x and y components separately.
R = A+B
RX = AX + BX eq 1
RY = AY + BY eq 2
Since, by rectangular components
R = RX + RX eq 3
Now, putting the values of eq 1 and eq 2 in eq 3
R = (AX + BX) + (AY + BY)
By rectangular component, the magnitude of the resultant vector is given as
|R| = √ ((Rx )2+( Ry)2)
|R| = √ ((Ax + BX )2+( Ay + BY)2)
By rectangular components direction of the resultant vector is defined as:
θ = tan-1 (RY / Rx)
The same method will be applicable for any number of vectors A, B, C, D…… to find out the resultant vector R.
R = A+B+C+……
RX = AX+BX+CX+…..
RY = AY+BY+CY+……
R = RX + RX
θ = tan-1 (RY / Rx)
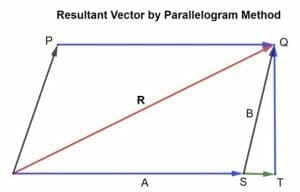
Finding Resultant Vector Using Parallelogram Method
According to the law of parallelogram vector addition:
“If two vectors acting, at once, at a point can be represented by the adjacent sides of a parallelogram drawn from a point, then the resultant vector is represented by the diagonal of the parallelogram passing through that point.”
Consider two vectors A and B acting at a point and represented by the two sides of a parallelogram as shown in the figure.
θ is the angle between vectors A and B, and R is said to be the resultant vector. Then, according to the parallelogram law of vector addition, the diagonal of the parallelogram represents the resultant of vectors A and B.
Mathematical Derivation
Below given is the mathematical derivation:
R=A+B
Now, expand S to T and draw QT perpendicular to OT.
From triangle OTQ,
SQ2=OT2+TQ2 eq 1.4
SQ2=(OS+ST)2+TQ2
In triangle STQ,
cosθ=ST/SQ
SQcosθ=ST
Also,
sinθ=TQ/SQ
TQ=SQsinθ
Putting in eq 1.4 gives,
|SQ|=√((A+SQsinθ)2+(SQcosθ)2)
Let, SQ=OP=D
|SQ||=√((A+Dsinθ)2+(Dcosθ)2)
Solving the above equation gives,
|SQ|= √(A2+2ADcosθ+D2)
So, |SQ| gives the magnitude of the resultant vector.
Now finding out the direction of the resultant vector,
tanφ = TQ/SQ
φ = tan-1 (TQ/OT)
tanφ = TQ/ (OS+ST)
tanφ = Dsinθ/A+Dcosθ
φ = tan –1(Dsinθ/A+Dcosθ)
Let’s have a better understanding with the help of an example.
Example 4
A force of 12N is making an angle of 45o with the positive x-axis, and the second force of 24N is making an angle of 120o with the positive x-axis. Calculate the magnitude of the resultant force.
Solution
By resolving the vector into its rectangular components, we know that
RX = F1X+F2X
RY= F1Y+F2Y
|R| = √ ((Rx )2+( Ry)2) eq 1.1
Calculating the values of |RX| and |RY|,
|Rx| = |F1X| + |F2X| eq 1.2
|F1X |=F1cosθ1
|F1X |=12cos45
|F1X |=8.48N
|F2X |=F2cosθ2
|F2X |=24cos120
|F2x|= -12N
Putting the values in eq 1.2 gives,
|Rx| = 8.48+(-12)
|Rx| = -3.52N
Now, finding the y-component of the resultant vector
|RY| = |F1Y| + |F2Y| eq 1.3
|F1Y |=F1sinθ1
|F1Y |=12sin45
|F1Y|=8.48N
|F2Y |=F2 sinθ2
|F2Y |=24sin120
|F2Y |= 20.78N
Putting the values in eq 1.2 gives,
|Ry | = 8.48+20.78
|Ry | = 29.26N
Now, putting the values in eq 1.1 to calculate the magnitude of the resultant vector R,
|R| = √ ((-3.52 )2+( 29.26)2)
|R| = √ (12.4+856.14)
|R| = 29.5 N
So, the magnitude of the resultant vector R is 29.5N.
Example 5
Two forces of magnitude 5N and 10N are inclined at an angle of 30o. Calculate the magnitude and direction of the resultant vector using parallelogram law.
Solution
Given that there are two forces F 1 = 5N and F 2 = 10N and angle θ=30o.
Using formula,
|R|= √(F12+2F1F2cosθ+F22)
|R|= √ ((5)2+2(5)(10) cos30+(10)2)
|R| =14.54N
φ = tan –1(F2sinθ/F1+F2cosθ)
φ = tan-1 (10sin30/(5+10cos30))
φ = 20.1o
So, the magnitude of the resultant vector R is 14.54N, and the direction is 20.1o.
Practice Problems
- Find out the resultant vector of the following vector parallel to each other, pointing in the same direction
- OA=12N, OB=24N (Ans: 36N )
- OA=7N, OB=10N (Ans: 17N )
- PQ= (3,8) RQ= (2,4) (Ans: (5, 12)
- A force of 15N is making an angle of 70o with the positive x-axis, and the second force of 25N is making an angle of 220o with the positive x-axis. Calculate the magnitude of the resultant force. (Ans: 37N )
- Calculate the direction of the resultant vector defined in problem no 3. (Ans: 21.80 )
- A force of 30N is acting at 25o towards the north-east. Another force of 45N acting at 60o. Calculate and draw the resultant vector. (Ans: 22N )
- Two forces of magnitude 12.7N and 35N are inclined at an angle of 345o. Calculate the magnitude and direction of the resultant vector using parallelogram law. (Ans: 38.3N)
All the vector diagrams are constructed by using GeoGebra.