- Home
- >
- Roots of complex numbers – Examples and Explanation
JUMP TO TOPIC
Roots of Complex Numbers – Examples and Explanation
 Complex numbers, as with real numbers, have roots too. We’ve learned how to solve equations in the past, but we’ve disregarded the complex roots. This time, we’ll focus our attention on finding all the roots – both real and complex.
Complex numbers, as with real numbers, have roots too. We’ve learned how to solve equations in the past, but we’ve disregarded the complex roots. This time, we’ll focus our attention on finding all the roots – both real and complex.
We can find the roots of complex numbers easily by taking the root of the modulus and dividing the complex numbers’ argument by the given root.
This means that we can easily find the roots of different complex numbers and equations with complex roots when the complex numbers are in polar form.
Make sure to review the following concepts before we jump right into finding the roots of different complex numbers:
- Converting complex numbers in the rectangular form to polar form, and the other way around.
- Understanding how De Moivre’s theorem works and applies to finding a complex number’s roots.
Check out the links we’ve provided as well in case we need to take a refresher. For now, why don’t we go ahead and dive right into the fundamentals of complex numbers and their roots?
What is the roots of complex numbers?
Given a complex number $z = a + bi$ or $z = r(\cos \theta + i\sin \theta)$, the complex numbers’ roots are equal to result of raising $z$ to the power of $\dfrac{1}{n}$.
The roots of complex numbers are the result of finding either $z^{\frac{1}{n}}$ or $z^n$. Keep in mind that when finding the $n$th root of $z$, we’re expecting $n$ roots as well.
This means that the cube root of $8$, we’re three roots including the real and complex roots. In fact, these three roots are: $2$, $-1 + \sqrt{3}i$, and $-1 – \sqrt{3}i$.
You’ll learn how to find these complex roots in the next sections, so why don’t we go ahead and jump right in?
How to find roots of complex numbers?
From De Moivre’s theorem, we’ve shown how we can find the roots of complex numbers in polar form. Let’s say we have $z =r(\cos \theta + i \sin \theta)$, we can find $\sqrt[n] z$ using the formula shown below.
| $\boldsymbol{\theta}$ in degrees | $\boldsymbol{\theta}$ in radians |
| $\sqrt[n]{z} = \sqrt[n]{r} \left(\cos \dfrac{\theta + 360^{\circ} k}{n} + i\sin \dfrac{\theta + 360^{\circ} k}{n}\right)$ | $\sqrt[n]{z} = \sqrt[n]{r} \left(\cos \dfrac{\theta + 2\pi k}{n} + i\sin \dfrac{\theta + 2\pi k}{n} \right )$ |
Since we’re looking for a total of $n$ roots for $\sqrt[n]{z}$, $k$ must be equal to $\{0, 1, 2, 3, …, n – 1\}$.
We can also find the roots of complex numbers by graphing the roots on a complex plane and plotting each root $\dfrac{2\pi}{n}$ or $\dfrac{360^{\circ}}{n}$ apart.
Don’t worry. We’ll break down the important steps in the next section to make sure we know how to find the roots of complex numbers algebraically and geometrically.
Finding roots of complex numbers
As we have mentioned, we can either find the roots using the formula derived from De Moivre’s theorem, or we can find the roots by graphing them on a complex plane.
Finding the roots of complex numbers geometrically.
Here are some helpful steps to remember when finding the roots of complex numbers.
- If the complex number is still in rectangular form, make sure to convert it to polar form.
- Find the $n$th root of $r$ or raise $r$ to the power of $\dfrac{1}{n}$.
- If we need to find the $n$th root, we’ll use $k = \{0, 1, 2… n-1\}$ in the formula we’ve provided above.
- Start by finding the argument of the first root by dividing $\theta$ by $n$.
- Repeat the same process, but this time, work with $\theta + 2\pi k$ or $\theta + 360^{\circ}k$ until we have $n$ roots.
Finding the roots of complex numbers geometrically.
It’s also possible to find the roots of complex numbers by graphing these roots on a complex plane.
- If the complex number is still in rectangular form, make sure to convert it to polar form.
- Divide $2\pi$ or $360^{\circ}$ by $n$.
- Draw the first root on the complex plane by joining the origin with a segment $r$ units long.
- Plot the first complex root by using the complex root formula, where $k = 0$.
- Draw the next root by making sure that it is $\dfrac{2\pi}{n}$ or $\dfrac{360^{\circ} }{n}$ apart from the next roots.
Are you ready to apply what you’ve just learned? Don’t worry; we’ve prepared some problems to try on and check your knowledge on complex number roots.
Example 1
Confirm that $8$ has indeed the following three complex roots: $2$, $-1 + \sqrt{3}i$, and $-1 – \sqrt{3}i$.
Solution
Let’s go ahead and confirm that $8$ has the following cube roots: $2$, $-1 + \sqrt{3}i$, and $-1 – \sqrt{3}i$ by using the steps shown above.
Since $8$ is still in its rectangular form, $8 = 8 + 0i$, we’ll have to convert it first to polar form by finding its polar form’ modulus and argument as shown below.
| $\boldsymbol{r = \sqrt{a^2 + b^2}}$ | $\boldsymbol{ \theta = \tan^{-1} \dfrac{b}{a}}$ |
| $\begin{aligned} r &= \sqrt{8^2 + 0^2}\\&= \sqrt{64}\\&=8\end{aligned}$ | $\begin{aligned} \theta &= \tan^{-1} \dfrac{0}{8}\\&= \tan^{-1} 0\\&= 0\end{aligned}$ |
This means that we start with $n = 3$, $k= 0$, and $\theta = 0$ for the formula, $\sqrt[n]{z} = \sqrt[n]{r} \left(\cos \dfrac{\theta + 2\pi k}{n} + i\sin \dfrac{\theta + 2\pi k}{n} \right )$.
$ \begin{aligned} \sqrt[3]{8} &= \sqrt[3]{8} \left(\cos \dfrac{0 + 2\pi \cdot 0}{3} + i\sin \dfrac{0 + 2\pi \cdot 0}{3} \right )\\&=2 (\cos 0 + i\sin 0 )\end{aligned}$
The root is still in polar form, so if we want the root in rectangular form, we can simply evaluate the result to convert it to rectangular form.
$ \begin{aligned} 2 (\cos 0 + i\sin 0 )&= 2(1 + 0i)\\&= 2 \end{aligned}$
This means that the first root of $8$ is $2$. We can apply the same process for the two remaining roots, but this, we use $k = 1$ and $k = 2$.
| $\boldsymbol{\sqrt[n]{z}}$ when $\boldsymbol{k = 1, 2}$ | $\boldsymbol{a + bi}$ |
| $ \begin{aligned} k = 1\\\\\sqrt[3]{8} &= \sqrt[3]{8} \left(\cos \dfrac{0 + 2\pi \cdot 1}{3} + i\sin \dfrac{0 + 2\pi \cdot 1}{3} \right )\\&=2 \left(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3} \right)\end{aligned}$ | $ \begin{aligned} 2 \left(\cos \dfrac{2\pi}{3} + i\sin \dfrac{2\pi}{3} \right) &= 2\left(-\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\right)\\&= -1 + \sqrt{3}i \end{aligned}$ |
| $ \begin{aligned}k = 2\\\\ \sqrt[3]{8} &= \sqrt[3]{8} \left(\cos \dfrac{0 + 2\pi \cdot 2}{3} + i\sin \dfrac{0 + 2\pi \cdot 2}{3} \right )\\&=2 \left(\cos \dfrac{4\pi}{3} + i\sin \dfrac{4\pi}{3} \right)\end{aligned}$ | $ \begin{aligned} 2 \left(\cos \dfrac{4\pi}{3} + i\sin \dfrac{4\pi}{3} \right) &= 2\left(-\dfrac{1}{2} – \dfrac{\sqrt{3}}{2}i\right)\\&= -1 – \sqrt{3}i \end{aligned}$ |
We’ve just shown $8$ has the following three complex roots: $2$, $-1 + \sqrt{3}i$, and $-1 – \sqrt{3}i$ in rectangular form.
Example 2
Plot the complex fourth roots of $-8 + 8\sqrt{3}i$ on one complex plane. Write down the roots in rectangular form as well.
Solution
Let’s start by finding the modulus and argument of the complex number, $-3 + 3\sqrt{3}i$.
| $\boldsymbol{r = \sqrt{a^2 + b^2}}$ | $\boldsymbol{ \theta = \tan^{-1} \dfrac{b}{a}}$ |
| $\begin{aligned} r &= \sqrt{(-8)^2 + (8\sqrt{3})^2}\\&= \sqrt{36}\\&=256\end{aligned}$ | $\begin{aligned} \theta &= \tan^{-1} \dfrac{8\sqrt{3}}{-8}\\&= \tan^{-1} -\sqrt{3}\\&= 120^{\circ}\end{aligned}$ |
Hence, $-8 + 8\sqrt{3}i = 16(\cos 120^{\circ} + i \sin 120^{\circ})$. Since we’re looking for the cube roots, we’re expecting roots to be $\dfrac{360^{\circ}}{4} = 90^{\circ}$ apart from each other.
We can use the complex root formula, $\sqrt[n]{z} = \sqrt[n]{r} (\cos \dfrac{\theta + 360^{\circ} k}{n} + i\sin \dfrac{\theta + 360^{\circ} k}{n})$, where we assign $n = 4$, $r = 6$, $\theta = 120^{\circ}$,and $k=0$.
$\begin{aligned} \sqrt[4]{16(\cos 120^{\circ} + i \sin 120^{\circ})}&= \sqrt[4]{16} \left(\cos \dfrac{120^{\circ} + 360^{\circ} \cdot 0}{4} + i\sin \dfrac{120^{\circ} + 360^{\circ} \cdot 0}{4} \right )\\&= 2 (\cos 30^{\circ} + i\sin 30^{\circ}) \end{aligned}$
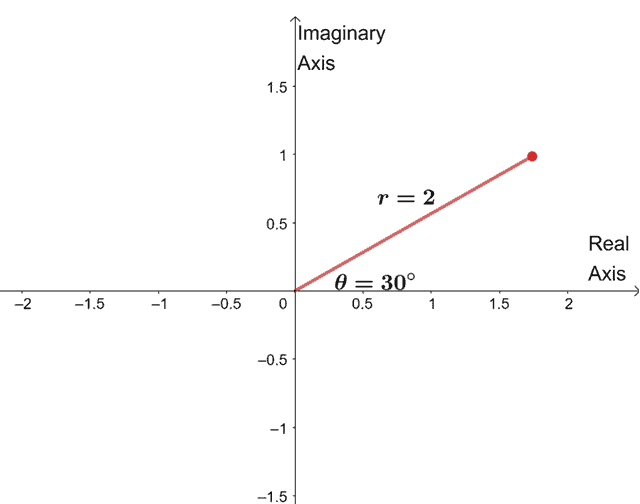
To find the three remaining roots, we graph three roots with the same modulus, $2$, and the arguments are each $90^{\circ}$ apart from each other.
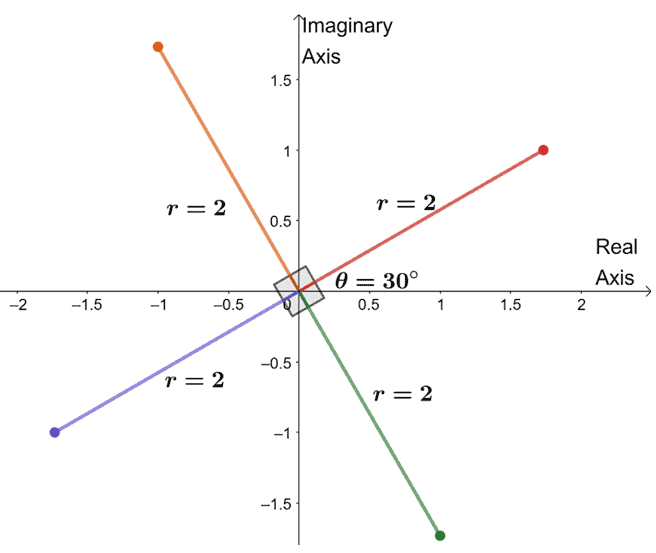
We’ve just graphed all the fourth root of the complex number. From this, we can even list down the four roots of $-8 + 8\sqrt{3}i$.
- $2(\cos 30^{\circ} + i \sin 30^{\circ})$
- $2(\cos 120^{\circ} + i \sin 120^{\circ})$
- $2(\cos 210^{\circ} + i \sin 210^{\circ})$
- $2(\cos 300^{\circ} + i \sin 300^{\circ})$
We can even convert the roots to rectangular form as shown by evaluating the cosine and sine values then distributing $2$ each time.
| Polar Form | Rectangular Form |
| $2(\cos 30^{\circ} + i \sin 30^{\circ})$ | $\begin{aligned} 2(\cos 30^{\circ} + i \sin 30^{\circ}) &= 2\left(\dfrac{\sqrt{3}}{2}+ \dfrac{1}{2}i\right) \\&= 2 \cdot \dfrac{\sqrt{3}}{2}+ 2\cdot \dfrac{1}{2}i \\&=\sqrt{3} + i \end{aligned}$ |
| $2(\cos 120^{\circ} + i \sin 120^{\circ})$ | $\begin{aligned} 2(\cos 120^{\circ} + i \sin 120^{\circ}) &= 2\left(-\dfrac{1}{2}+ \dfrac{\sqrt{3}}{2}i\right) \\&= 2 \cdot -\dfrac{1}{2}+ 2\cdot \dfrac{\sqrt{3}}{2} i \\&=-1 + \sqrt{3}i \end{aligned}$ |
| $2(\cos 210^{\circ} + i \sin 210^{\circ})$ | $\begin{aligned} 2(\cos 210^{\circ} + i \sin 210^{\circ}) &= 2\left(-\dfrac{\sqrt{3}}{2}- \dfrac{1}{2}i\right) \\&= 2 \cdot -\dfrac{\sqrt{3}}{2}- 2\cdot \dfrac{1}{2} i \\&=-\sqrt{3} – i \end{aligned}$ |
| $2(\cos 300^{\circ} + i \sin 300^{\circ})$ | $\begin{aligned} 2(\cos 300^{\circ} + i \sin 300^{\circ}) &= 2\left(\dfrac{1}{2}- \dfrac{\sqrt{3}}{2}i\right) \\&= 2 \cdot \dfrac{1}{2}- 2\cdot \dfrac{\sqrt{3}}{2} i \\&=1 – \sqrt{3}i \end{aligned}$ |
Hence, we’ve just shown that we can find the remaining roots geometrically and even convert the result in rectangular form.
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
