Rules of Divisibility – Methods & Examples

Division is one of the four basic operations which distributes a number into equal parts. It is a mathematical technique where a number is shared into smaller groups or a technique of distributing quantities into equal parts.  It is denoted by several symbols: the slash, the horizontal line, and the division sign.

The division is an inverse operation of multiplication. For example, the multiplication of 5 by 2 gives 10. You can obtain either of the factors 2 and 5 by dividing 10 by any of the numbers.

What is a Rule of Divisibility?

Divisibility rules have been developed to make the division process easier and quicker. Understanding divisibility rules for 1 up to 20 is an important skill in mathematics as it enables you to solve problems in a better way.

For, instance the divisibility rule for number 9 will definitely tell us whether the number is divisible by 9, no matter how big the number may seem to be.

You can easily memorize divisibility rules for numbers such as 2, 3, 4, and 5. But the divisibility rules for 7, 11, and 13 are a bit complex, and for this reason, there is a need to understand them elaborately.

Divisibility Rules

As the name suggests, divisibility rules or tests are procedures used to check whether a number is divisible by another number without necessarily performing the actual division. A number is divisible by another number if the results or quotient is a whole number and the remainder is zero.

Since not all numbers are completely divisible by other numbers, the divisibility rules are actually the shortcuts of determining a number’s actual divisor just by examining the digits that make the number.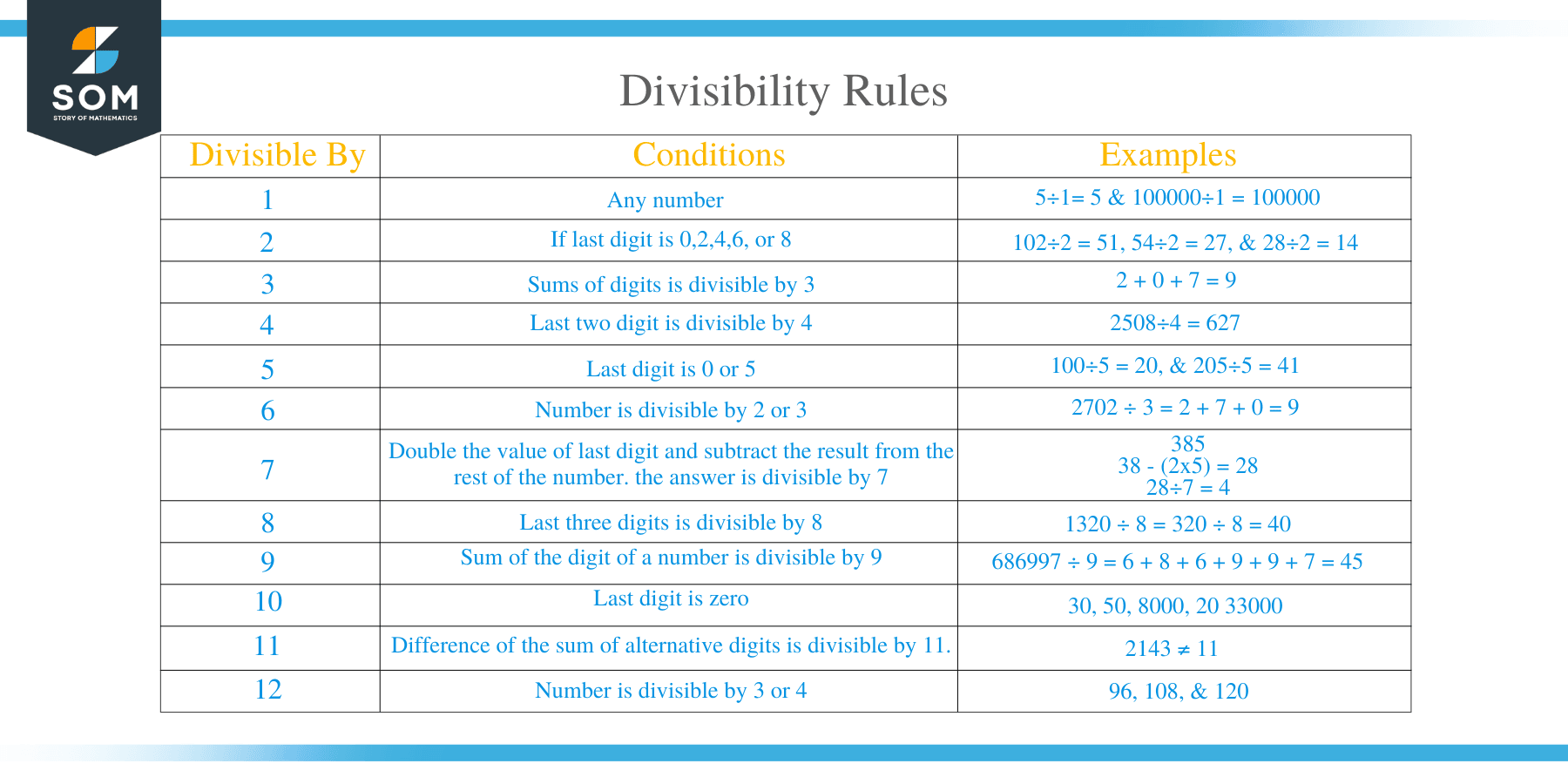

Let us now look into these divisibility rules for different numbers.

• Divisibility rule for 1

The divisibility test for 1 does not have any condition for numbers. All numbers are divisible by 1, irrespective of how large the numbers are. When any number is divided by 1, the result is the number itself. For example, 5/1= 5 and 100000/1 = 100000.

• Divisibility test for 2

A number is divisible by 2 if the last digit of the number is 2, 4, 6, 8, or 0.

For example: 102/2 = 51, 54/2 = 27, 66/2 = 33, 28/2 = 14 and 20/2 = 10

• Divisibility Rules for 3

The divisibility test for 3 states that a number is completely divisible by 3 if the number’s digits are divisible by 3 or is a multiple of 3.

For example, consider two numbers, 308 and 207:

To check if 308 is divisible by 3 or not, find the sum of the digits.

3+0+8= 11. Since the sum is 11, which not divisible by 3, then 308 is also not divisible by 3.

Check 207 by summing its digits: 2 + 0 + 7 = 9, since 9 is a multiple of 3, then 207 is also divisible by 3.

• Divisibility test for 4

The divisibility test for 4 states that a number is divisible by 4 if the last two digits of the number are divisible by 4,

For example: Consider two numbers, 2508 and 2506.

The last digits of the number 2508 are 08. Since 08 is divisible by 4, then the number 2508 is also divisible by 4.

2506 is not divisible by 4 because the last two digits, 06, are not divisible by 4.

• Divisibility test for 5

All numbers with the last digit as 0 or 5 are divisible by 5. For example, 100/5 = 20, 205/5 = 41.

• Divisibility test for 6

A number is divisible by 6 if its last digit is an even number or zero and the sum of the digits is a multiple of 3.

For example, 270 is divisible by 2 because the last digit is 0.

The sum of the digits is: 2 + 7 + 0 = 9 which is also divisible by 3.

Therefore, 270 is divisible by 6.

• Divisibility Rules for 7

The divisibility test of 7 is explained in the following algorithm

Consider a number 1073. To check whether the number is divisible by 7 or not?

Eliminate number 3 and multiply it by 2, which becomes 6. Subtract 6 from the remaining number 107, therefore 107 – 6 = 101.

Repeat the process. We have 1 x 2 = 2, and the remaining number is 10 – 2 = 8. Since 8 is not divisible by 7, therefore the number 1073 is also not divisible by 7.

• Divisibility by 8

The divisibility test for 8 states that a number is divisible by 8 if its last three digits are divisible by 8.

• Divisibility test for 9

The divisibility test for 9 is the same as the divisibility test for 3. If the sum of the digits of a number is divisible by 9, then the number is also divisible by 9.

Example: In a number like 78532, the sum of its digits is: 7+8+5+3+2 = 25. Since 25 is not divisible by 9, the 78532 is also not divisible by 9. Considering another case of number: 686997, the sum of digits is: 6 + 8 + 6 + 9 + 9 + 7 = 45. Since the sum is divisible by 9, then the number 686997 is divisible by 9.

• Divisibility test for 10

The divisibility rule for 10 states that any number whose last digit is zero, then the number I divisible by 10.

For example, The numbers: 30, 50, 8000, 20 33000 are divisible by 10.

• Divisibility Rules for 11

This rule states that a number is divisible by 11 if the difference of the sum of alternative digits is divisible by 11.

For example, to check whether number 2143 is divisible by 11 or not, the procedure is:

The sum of alternative digits of each group is: 2 + 4 = 6 and 1+ 3 = 4

Therefore, 6-4 = 2, and so the number is not divisible by 11. Therefore 2143 is not divisible by 11.

• Divisibility Rules for 13

To check whether a number is divisible by 13, repeated addition of the last digit is done 4 times to the remaining number until a two-digit number is arrived at. If the two-digit number is divisible by 13, then the whole number is also divisible by 13.

For example:

2795 → 279 + (5 x 4) → 279 + (20) → 299 → 29 + (9 x 4) → 29 + 36 →65.

In this case, the two-digit number is found to be 65 which is divisible by 13, therefore, the number 2795 is also divisible by 13.