- Home
- >
- Sas Triangle – Explanation & Examples
SAS Triangle – Explanation & Examples
Oblique triangles do not have any right angles. When solving oblique triangles, we must first know the measure of at least one leg and the measure of the other two parts of the oblique triangle: two angles, two legs, or one side and one angle. In simple words, we can get a lot of different combinations when solving the oblique triangles. One of these combinations or attributes is the SAS triangle.
What Is a SAS Triangle?
Consider a triangle $△ABC$ with the sides $a$, $b$, and $c$ facing the angles $\alpha$, $\beta$, and $\gamma$, respectively, as shown in Figure 15-1. We can observe that we are given two sides $b$ and $c$, and the included angle $\alpha$. Figure 14-1 illustrates a triangular combination which is known as a SAS triangle.
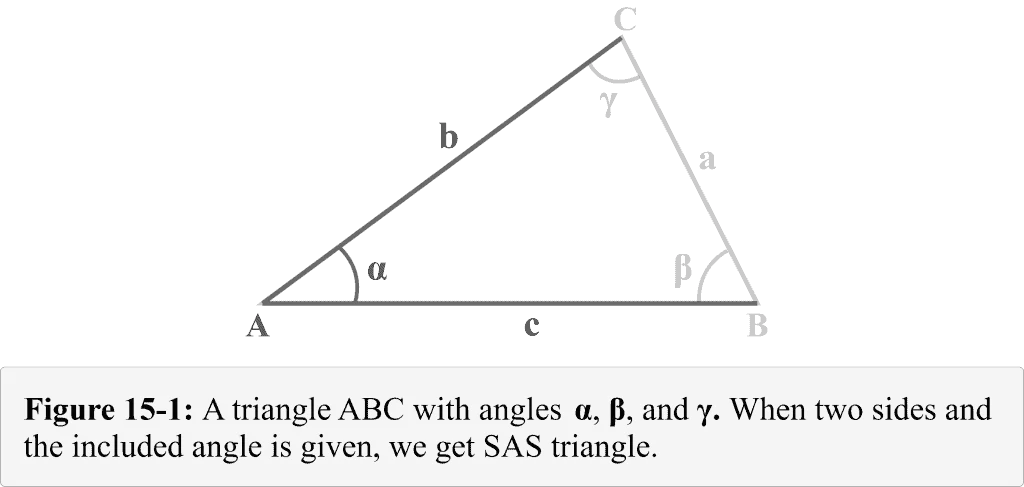
How To Solve a SAS Triangle?
When we know the measure of two sides and the included angle, we can apply a three-step method to solve a SAS triangle: using the Law of Cosines, using the Law of Sines, and determining the measure of the third angle.
Step 1 of 3
- Use the Law of Cosines to measure the missing side.
Step 2 of 3
- Use the Law of Sines to find the angle (acute angle) opposite the smaller of the two sides.
Step 3 of 3
- Determine the measure of the third angle by subtracting the already measured angles (given angle and the angle determined in step 2) from $180^{\circ }$.
Example 1
In triangle $△ABC$, $m∠\alpha = 60^{\circ }$, $b = 2$ and $c = 3$. Solve the triangle.
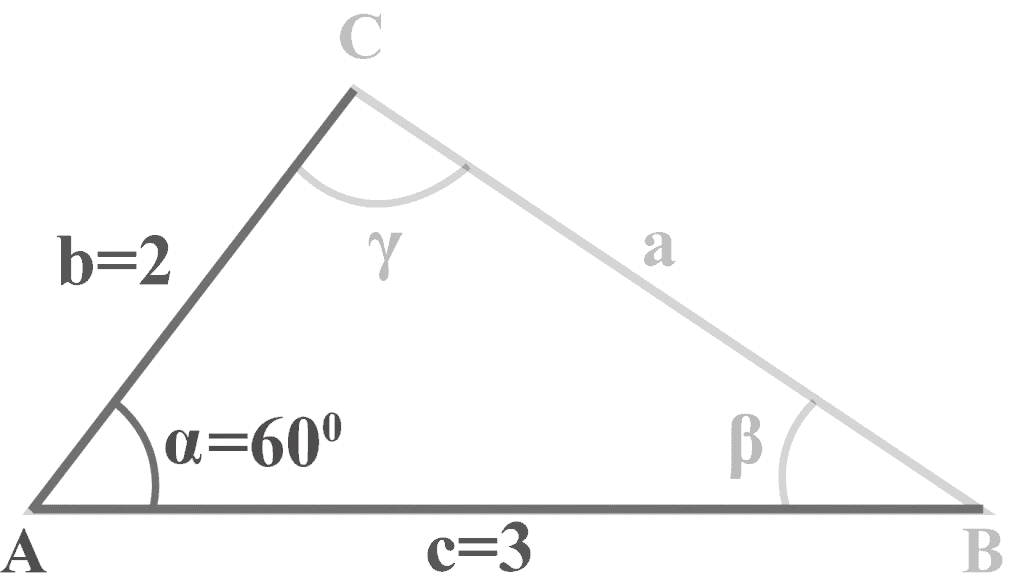
Solution:
We are given two sides $b = 2$, $c = 3$, and an angle $m∠\alpha = 60^{\circ }$. To solve the SAS triangle, we will apply this three-step method.
Step 1 of 3
Use the Law of Cosines to measure the missing side.
First, we need to determine the missing side $a$.
Applying the law of cosines
$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:\alpha$
substituting $b = 2$, $c = 3$ and $\alpha = 60^{\circ }$ in the formula
$a^2\:=\:(2)^2\:+(3)^2\:-\:2(2)(3)\:\cos\:60^{\circ }$
$a^2 = 4\:+\:9-12\:\left(0.5\right)$
$a^2 = \:13-6\:$
$a^2 = 7$
$a=\sqrt{7}$
$a ≈ 2.6$ units
Step 2 of 3
Use the Law of Sines to find the angle (acute angle) opposite the smaller of the two sides.
The smaller of the two given sides is $b = 2$. Thus, we will have to determine acute angle $\beta$.
Applying the law of sines
$\frac{a}{\sin\:\alpha\:}=\:\frac{b}{\sin\:\beta}$
substitute $b = 2$, $a = 2.6$ and $\alpha = 60^{\circ }$
$\frac{2.6}{\sin\:60^{\circ }\:}=\:\frac{2}{\sin\:\beta}$
$\sin\:\beta=2\:\frac{\left(\sin\:60^{\circ }\right)}{2.6}\:$
$\sin\:\beta=2\:\frac{\left(0.866\right)}{2.6}\:$
$\sin\: \beta = 0.6661$
$\beta = \sin^{-1} (0.6661)$
$\beta = 41.7667…^{\circ }$
$\beta ≈ 41.8^{\circ }$
Step 3 of 3
Determine the measure of the third angle by subtracting the already measured angles (given angle and the angle determined in step 2) from 180º.
$\gamma = 180^{\circ }\: – \alpha\: – \beta$
substitute $\alpha = 60^{\circ }$ and $\beta = 41.8^{\circ }$
$\gamma = 180^{\circ }\: -\: 60^{\circ }\: –\: 41.8^{\circ }$
$\gamma = 78.2^{\circ }$
Thus, the solution of the given SAS triangle is:
$a = 2.6$ units, $\beta = 41.8^{\circ }$, and $\gamma = 78.2^{\circ }$
Example 2
In triangle $△ABC$, $m∠\beta = 110^{\circ }$, $a = 5$ and $c = 7$. Solve the triangle.
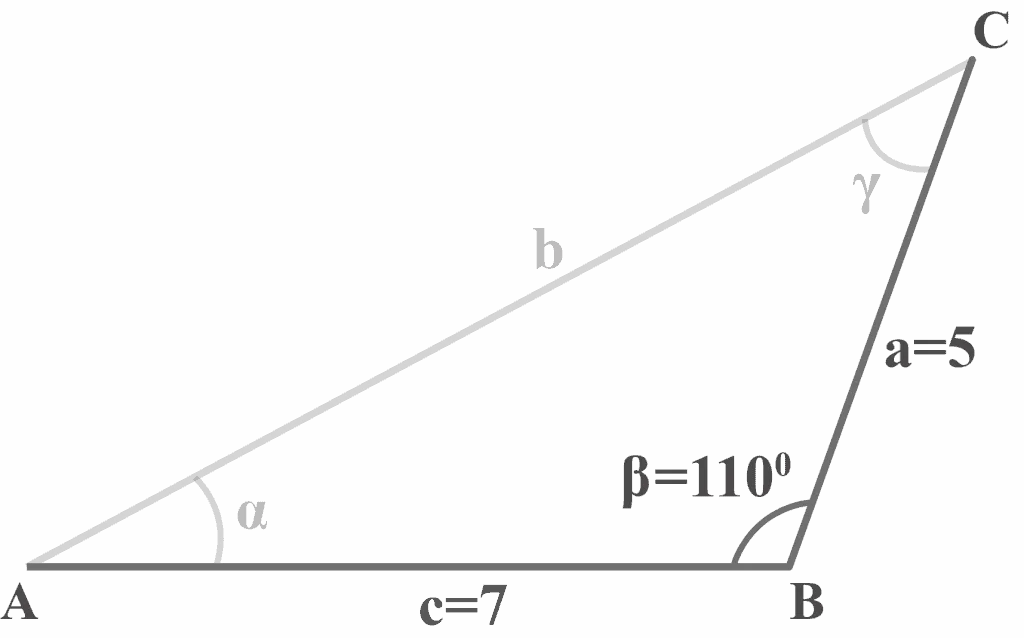
Solution:
We are given two sides $a = 5$, $c = 7$, and an angle $m∠\beta = 110^{\circ }$. We will apply the three-step method to solve a SAS triangle.
Step 1 of 3
First, we need to determine the missing side $a$.
Applying the law of cosines
$b^2\:=\:c^2\:+a^2\:-\:2ca\:\cos\:\beta$
substituting $a = 5$, $c = 7$ and $\beta = 110^{\circ }$ in the formula
$b^2\:=\:(7)^2\:+(5)^2\:-\:2(7)(5)\:\cos\:110^{\circ }$
$b^2 = 49\:+\:25-70\:\left(-0.342\right)$
$b^2 = \:74+23.94\:$
$b^2 = 97.94$
$b ≈ 9.9$ units
Step 2 of 3
The smaller of the two given sides is $a = 5$. Thus, we will have to determine acute angle $\alpha$.
Applying the law of sines
$\frac{a}{\sin\:\alpha\:}=\:\frac{b}{\sin\:\beta}$
substitute $a = 5$, $b = 9.9$ and $\beta = 110^{\circ }$
$\frac{5}{\sin\:\alpha\:}=\:\frac{9.9}{\sin\:110^{\circ }}$
$\sin\:\alpha=5\:\frac{\left(\sin\:110^{\circ }\right)}{9.9}\:$
$\sin\:\alpha=5\:\frac{\left(0.940\right)}{9.9}\:$
$\sin\:\alpha = 0.475$
$\alpha = \sin^{-1} (0.475)$
$\alpha = 28.3593…^{\circ }$
$\alpha ≈ 28.4^{\circ }$
Step 3 of 3
Subtract the given angle $\beta = 110^{\circ }$ and the measured angle $\alpha = 28.4^{\circ }$ from $180^{\circ }$ to determine the third angle
$\gamma = 180^{\circ }\: – \alpha\: – \beta$
substitute $\alpha = 28.4^{\circ }$ and $\beta = 110^{\circ }$
$\gamma = 180^{\circ }\: -\: 28.4^{\circ }\: –\: 110^{\circ }$
$\gamma = 41.6^{\circ }$
Thus, the solution of the given SAS triangle is:
$a = 9.8$ units, $\alpha = 28.4^{\circ }$, and $\gamma = 41.6^{\circ }$
Example 2
From the Rome Airport, the two airplanes L and M leave simultaneously on different runways. Airplane L flies at a bearing of $N65^{\circ }W$ at $500$ km per hour and airplane M flies at a bearing of $S27^{\circ }W$ at $450$ km per hour. What will be the distance between the airplanes after three hours?
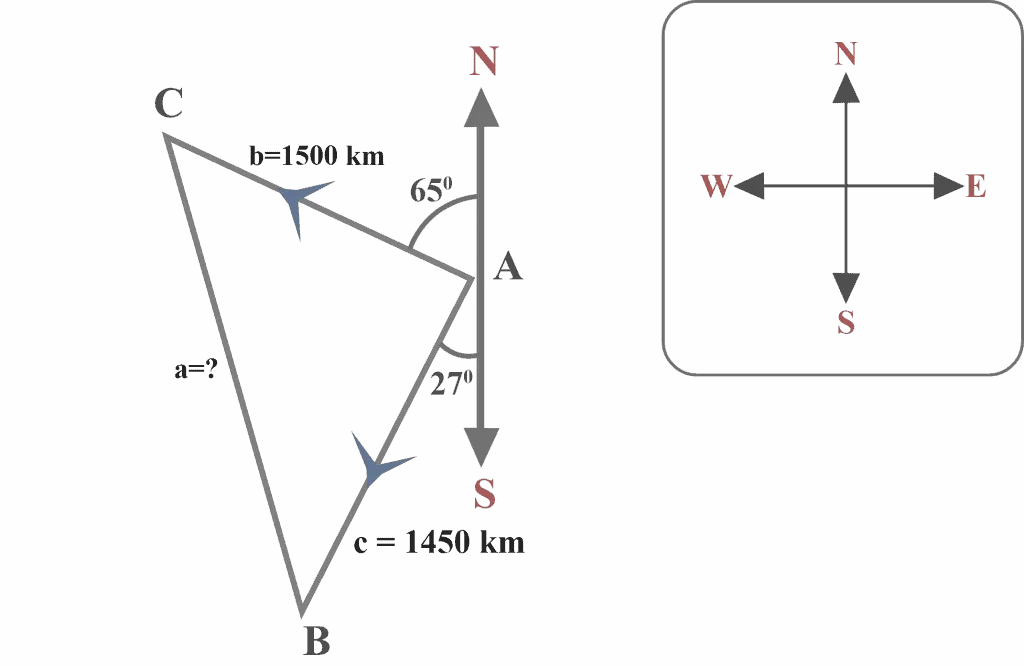
Solution:
Looking at the diagram, we can observe that:
Speed of airplane $L = 500$ km per hour
Distance covered by the airplane L after $3$ hours $= 500 × 3 = 1500$ km
Speed of airplane $M = 450$ km per hour
Distance covered by the airplane M after $3$ hours $= 450 × 3 = 1350$ km
Let the distance between the airplane $L$ and airplane $M$ after three hours $= a$
We know that a straight line measures $180^{\circ }$. Thus, we may use the North-South line to determine the measure of angle A in triangle $△ABC$. Thus,
$m∠A = 180^{\circ } – 65^{\circ } – 27^{\circ }$
$= 88^{\circ }$
Thus, we now have
$b = 1500$, $c = 1350$, and $m∠A = 88^{\circ }$
Thus, we have a SAS case here.
We now have to apply the Law of Cosines to determine $a$.
$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:\alpha$
substituting $b = 1500$, $c = 1350$ and $\alpha = 88^{\circ }$ in the formula
$a^2\:=\:(1500)^2\:+(1350)^2\:-\:2(1500)(1350)\:\cos\:88^{\circ }$
$a^2 = 2250000\:+\:1822500-4050000\:\left(0.035\right)$
$a^2 = \:4072500-141750\:$
$a^2 = 3930750$
$a ≈ 1982.6$ units
Therefore, the distance between the airplanes is approximately $1982.6$ km after three hours.
