Secant Cosecant Cotangent – Explanation & Examples

Secant, cosecant, and cotangent are trigonometric functions derived from the three elementary functions sine, cosine, and tangent. This article will explain secant, cosecant, and cotangent functions, calculate them, find their signs, and finally give several examples with explanations.

Since we are working with derived trigonometric functions, it will be helpful to go through the following topics if you think you need a refresher:

1. Basics of geometry, angles, and triangles.
2. Basics of trigonometry, sine, cosine, and tangent.

After reading this article, you should be able to:

1. Understand what secant, cosecant, and cotangent are.
2. Calculate these trigonometric ratios if a right-angled triangle is given.
3. Find these ratios for a given angle using a calculator.
4. Understand when and why a ratio is negative.
5. Evaluate the sign of a ratio without using a calculator.

What are secant cosecant and cotangent?

Let us visualize a right-angled triangle:

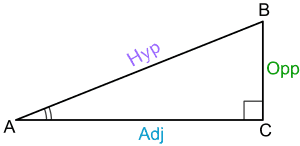
Let us denote the side adjacent to the angle $\theta$ by “Adj” and the side opposite to by “Opp.” The third side opposite the right-angle is called the hypotenuse, and we denote it by “Hyp.”

Secant:

Secant is defined as the reciprocal of cosine. The formula for cosine is:

So, we can write Secant as:

Cosecant:

Cosecant is defined as the reciprocal of sine. The formula for sine is:

So, we can write cosecant as:

Cotangent:

Cotangent is defined as the reciprocal of a tangent. The formula for tangent is:

So, we can write cotangent as

How to calculate secant cosecant and cotangent?

Suppose we are given a right-angled triangle as shown below:

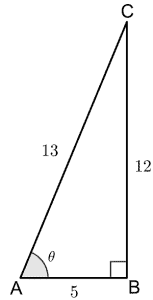
We first identify the values of Hyp, Adj, and Opp. From the above figure, we can see that Adj=5, Opp=12, and Hyp=13. We can calculate secant, cosecant, and cotangent as follows:

$ \large sec\left(\theta\right)=\frac{\textrm{Hyp}}{\textrm{Adj}}=\frac{13}{5}$

$\large csc\left(\theta\right)=\frac{\textrm{Hyp}}{\textrm{opp}}=\frac{13}{12}$

$\large cot\left(\theta\right)=\frac{\textrm{Adj}}{\textrm{opp}}=\frac{5}{12}$

If we are only given an angle and not the entire triangle, we can still find the value of cosecant, secant, and cotangent using a calculator. Most of the calculators only contain buttons for cos, sine, and tangent, so we calculate the values of cosecant, secant, and cotangent by taking the reciprocal of sin, cos, and tangent respectively.

For example, let us say we need to find the cosecant, secant, and cotangent values of 30°. Using a calculator, we find that, $cos\left({30}^\circ\right)=\ 0.866, $ the value of $sec\left({30}^\circ\right)$ is then

$sec\left({30}^\circ\right)=\frac{1}{cos\left({30}^\circ\right)}=\frac{1}{0.866}\ =\ 1.154$

Similarly, $sin\left({30}^\circ\right)=0.5$ and hence

$csc\left({30}^\circ\right)=\frac{1}{sin\left({30}^\circ\right)}=\frac{1}{0.5}=2$

Finally, $tan\left({30}^\circ\right)=\ 0.577$ and so

$cot\left({30}^\circ\right)=\frac{1}{tan\left({30}^\circ\right)}=\frac{1}{0.577}\ =\ 1.732$

In the table below, we list the values of secant, cosecant and cotangent for various values of $\theta$

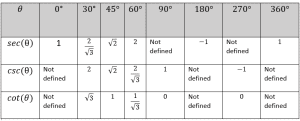
Why is the value “not defined” for secant, cosecant, or cotangent for some angles?

To understand this, note that $sin{\left(0^\circ\right)}=0$; therefore, $\ csc\left(0^\circ\right)=\frac{1}{sin{\left(0^\circ\right)}}=\frac{1}{0} $ which is undefined. Similarly, $tan{\left(0^\circ\right)}=0$ and $cos{\left({90}^\circ\right)}=0$, hence $cot{\left(0^\circ\right)}$ and $sec{\left({90}^\circ\right)}$ are not defined.

Radians and degrees:

We have used angles in degrees in this article; however, another popular unit for angles is radians. When using a calculator, make sure to check if the input mode is set to degrees or radians. It is relatively easy to convert degrees to radians and vice versa. The only thing you need to remember is that $ {360}^\circ=2\pi\ rad$. So, we can write: $1^\circ=\frac{2\pi}{360}\ rad$.

Now, if we need to convert, say $ {75}^\circ$ into radians, we simply calculate:

Signs of secant cosecant and cotangent

Let us put $\theta=\ 135^\circ$ in the calculator and try to find out the secant, cosecant, and cotangent values. We get $csc\left(\theta\right)=1.414$, $sec\left(\theta\right)=-1.414$ and $cot\left(\theta\right)=-1$. Note that both secant and cotangent have got negative values for $\theta=\ 135^\circ$. How can the value of a trigonometric ratio be negative? As we have defined above, all trigonometric ratios are ratios of the sides of a right-angled triangle’s lengths. Since the length is always positive, shouldn’t the trigonometric ratios be positive as well?

Another interesting question is, “How can we draw a right-angle triangle with one angle equal to 135?” We know from basic geometry that the sum of all angles of any triangle must be equal to 180°. Now one angle of a right-angle triangle is always 90° (by definition). If another angle is 135°, then we have 90°+135° = 225°, which is already greater than 180°, and we still have not added the third angle yet. What is happening here?
To understand the concept of negative trigonometric ratios, we first must understand how to draw a right-angled triangle for $\theta > 90^\circ$. To draw such a triangle, we use the concept of an x-y plane, as shown below. We divide the entire x-y plane into four quadrants:

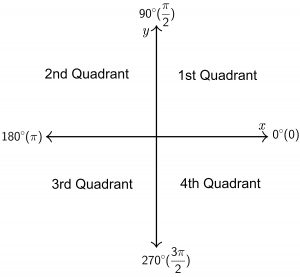
1. The first quadrant contains angles between 0° to 90°, and both x and y are positive in this quadrant.
2. The second quadrant contains angles between 90° to 180° and x is negative, and y is positive in this quadrant.
3. The third quadrant contains angles between 180° to 270°, and both x and y are negative in this quadrant.
4. The fourth quadrant contains angles between 270° to 360° and x is positive, and y is negative in this quadrant.

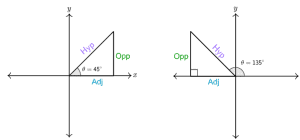
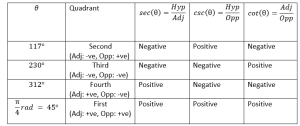
Now we draw a right-angle triangle corresponding to $\theta=\ 45^\circ$ and $\theta=\ 135^\circ$, in the x-y plane as shown below. First, we note that both triangles look the same, with the only difference that for $\theta=\ 135^\circ$, the triangle lies in the second quadrant, so the Adj is negative, and Opp is positive. Therefore, $sec{\left(\theta\right)}=\frac{\textrm{Hyp}}{\textrm{Adj}}$ and $cot{\left(\theta\right)}=\frac{\textrm{Adj}}{\textrm{Opp}}$ will have negative values; whereas, $csc{\left(\theta\right)}=\frac{\textrm{Hyp}}{\textrm{Opp}}$ will have a positive value.

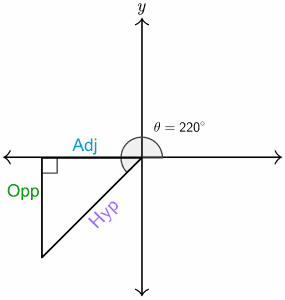
Now we draw a right-angle triangle with $\theta=\ 225^\circ$, and we get the same right-angled triangle but this time in the third quadrant. The length of both Adj and Opp are negative in this quadrant. Therefore, $csc{\left(\theta\right)}=\frac{\textrm{Hyp}}{\textrm{Opp}} $and $sec{\left(\theta\right)}=\frac{\textrm{Hyp}}{\textrm{Adj}}$ are both negative; whereas, $cot{\left(\theta\right)}=\frac{\textrm{Adj}}{\textrm{Opp}} $will be positive.

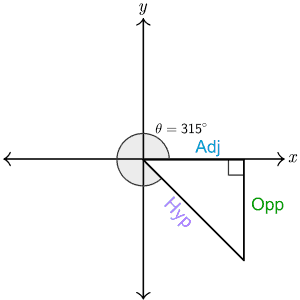
Finally, let us draw a triangle with $\theta=\ 315^\circ$. This time we get the same right-angled triangle in the fourth quadrant. Since Adj is positive and Opp is negative in this quadrant so $csc{\left(\theta\right)}=\frac{\textrm{Hyp}}{\textrm{Opp}}$ is negative, $sec{\left(\theta\right)}=\frac{\textrm{Hyp}}{\textrm{Adj}}$ is positive and $cot{\left(\theta\right)}=\frac{\textrm{Adj}}{\textrm{Opp}}$ is negative in the fourth quadrant.

The signs of the trigonometric identities for various angles and their corresponding quadrants are summarized in the table below:

Examples:

Example 1: For the given triangle, find the values of secant, cosecant, and cotangent.

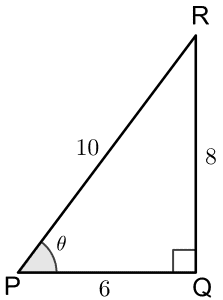
Solution:

We see that Adj=6, Opp=8, and Hyp=10. Now we can use the respective formulas for secant, cosecant, and cotangent as follows:

Example 2: Find the value of secant, cosecant, and cotangent for $\theta=\ 120^\circ$, using a calculator.

Solution:
Using a calculator, we find that $cos\left({120}^\circ\right)=\ -0.5$,
The value of $sec\left({120}^\circ\right)$ can then be found as

$sec\left({120}^\circ\right)=\frac{1}{cos\left({120}^\circ\right)}=\frac{1}{-0.5}\ =\ -2$

Similarly, $sin\left({120}^\circ\right)=0.866$ and hence

$csc\left({120}^\circ\right)=\frac{1}{sin\left({120}^\circ\right)}=\frac{1}{0.866}=1.15$

Finally, $\tan \left({120}^\circ \right)=-1.73$ and so

$cot\left({120}^\circ\right)=\frac{1}{tan\left({120}^\circ\right)}=\frac{1}{-1.73}\ =\ -0.57$

Example 3: Without using a calculator, find the sign of secant, cosecant, and cotangent for $\theta=117^\circ,230^\circ,312^\circ, \frac{\pi}{4}\ rad$

Solution: