Simplifying Rational Expressions – Explanation & Examples

Now that you understand what rational numbers are, the next topic to look at in this article is rational expressions and how to simplify them. Just for your own benefit, we define a rational number as a number expressed in the form of p/q where it is not equal to zero.

In other words, we can say a rational number is nothing more than a fraction in which the numerator and the denominator are integers. Examples of rational numbers are 5/7, 4/9/ 1/ 2, 0/3, 0/6 etc.

On the other hand, a rational expression is an algebraic expression of the form f(x) / g(x) in which the numerator or denominator are polynomials, or both the numerator and the numerator are polynomials.

Examples of rational expression are 5/x − 2, 4/(x + 1), (x + 5)/5, (x² + 5x + 4)/(x + 5), (x + 1)/(x + 2), (x² + x + 1)/2x etc.

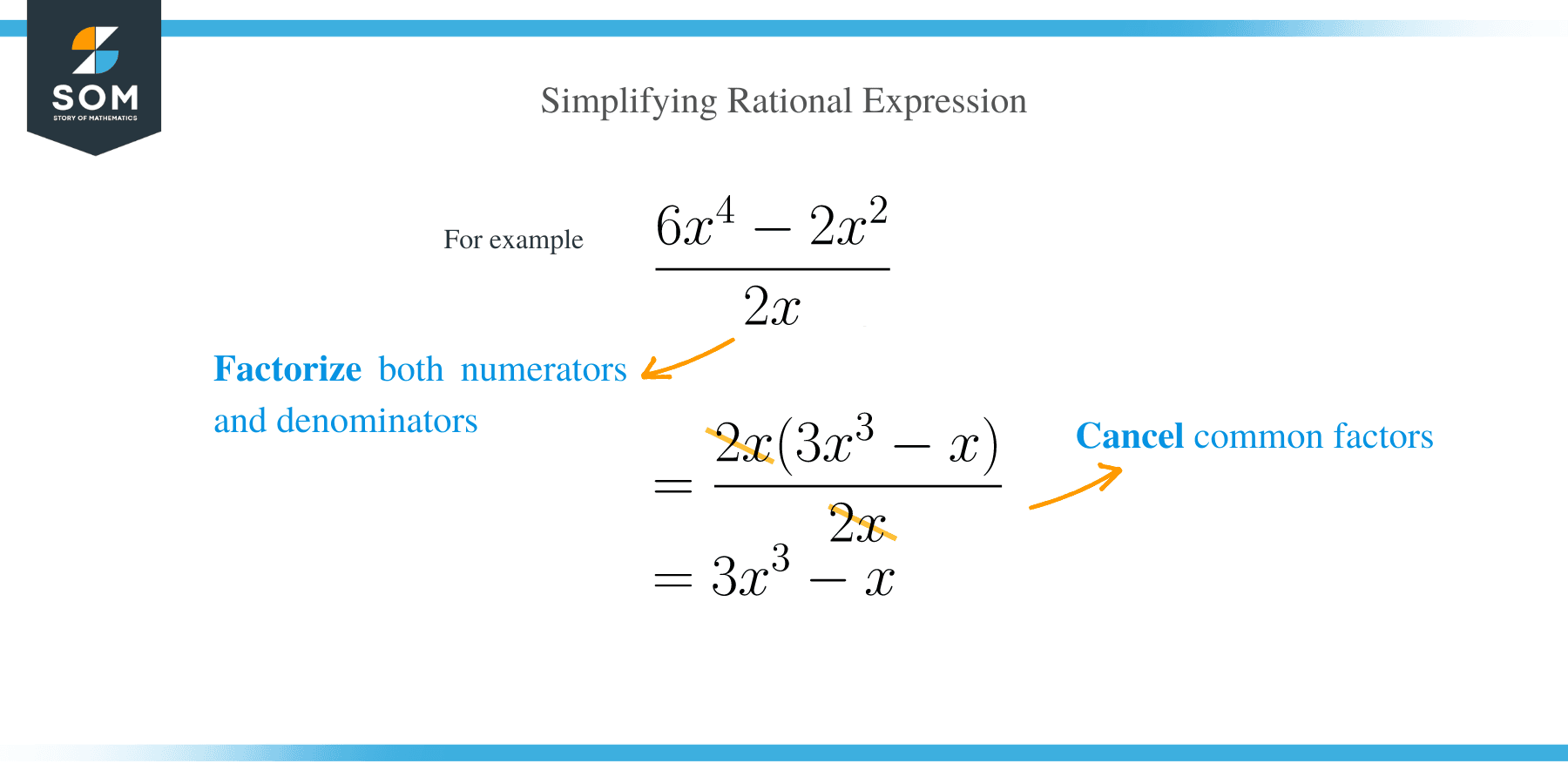
How to Simplify Rational Expressions?

Simplification of rational expression is the process of reducing a rational expression in its lowest terms possible. Rational expressions are simplified in the same way in which numerical numbers or fractions are simplified.

To simplify any rational expressions, we apply the following steps:

• Factorize both the denominator and numerator of the rational expression. Remember to write each expression in standard form.
• Reduce the expression by cancelling out common factors in the numerator and denominator
• Rewrite the remaining factors in the numerator and denominator.

Let’s simplify a couple of examples as shown below:

Example 1

Simplify: (x² + 5x + 4) (x + 5)/(x² – 1)

Solution

Factoring the numerator and denominator to get;

⟹ (x + 1) (x + 4) (x + 5)/(x + 1) (x – 1)

Now cancel the common terms.

⟹ (x + 4) (x + 5)/(x – 1)

Example 2

Simplify (x² – 4) / (x²+ 4x + 4)

Solution

Factor both the numerator and denominator to get.

⟹ (x + 2) (x – 2) / (x + 2) (x + 2)

Now cancel out common factors in the numerator and denominator to get.

= (x – 2) / (x + 2)

Example 3

Simplify the rational expression x / (x² – 4x)

Solution

Factor x out in the denominator to get;

⟹x /x (x – 4)

On cancelling the common terms in the top and bottom, we get;

= 1 / (x – 4)

Example 4

Simplify the rational expression (5x + 20) / (7x + 28)

Solution

Factor out the GCF in both the numerator and denominator;

= (5x + 20) / (7x + 28) ⟹ 5(x + 4) / 7(x + 4)

On cancelling common terms, we get;

= 5/7

Example 5

Simplify the rational expression (x² + 7x + 10) / (x² –  4)

Solution

Factor both the top and bottom of the expression.

= (x² + 7x + 10) / (x² –  4) ⟹ (x + 5) (x + 2) / (x² – 2²)

⟹ (x + 5) (x + 2) / (x + 2) (x – 2)

Cancel the common terms to get;

= (x + 5) / (x – 2)

Example 6

Simplify (3x + 9) / (3x + 15)

Solution

= (3x + 9) / (3x + 15) ⟹ 3(x + 3) / 3(x + 5)

= (x + 3) / (x + 5)

Example 7

Simplify the rational expression (64a³ + 125b³) / (4a²b + 5ab²)

Solution

Factor the numerator and the top;

= (64a³ + 125b³) / (4a²b + 5ab²) ⟹ [(4a)³ + (5b)³] / ab (4a + 5b)

⟹ (4a + 5b) [(4a)² – (4a) (5b) + (5b)²] / ab (4a + 5b)

Cancel out common terms to get;

= (16a² – 20ab + 25b²) / ab

Example 8

Simplify the following rational expression

(9x² – 25y²) / (3x² – 5xy)

Solution

= (9x² – 25y²) / (3x² – 5xy) ⟹ [(3x)² – (5y)²] / x (3x – 5y)

= [(3x + 5y) (3x – 5y)] / x (3x – 5y)

= (3x + 5y) / x

Example 9

Simplify: (6x² – 54) / (x² + 7x + 12)

Solution

= (6x² – 54) / (x² + 7x + 12)

= 6(x² – 9) / (x + 3) (x + 4)

= 6(x² – 3²) / (x + 3) (x + 4)

= 6(x + 3) (x – 3) / (x + 3) (x + 4)

= 6(x – 3) / (x + 4)