Simplifying Square Roots – Techniques and Examples

The square root is an inverse operation of squaring a number. The square root of a number x is denoted with a radical sign √x or x ^1/2. A square root of a number x is such that a number y is the square of x, simplify written as y² = x.

For instance, the square root of 25 is represented as √25 = 5. A number whose square root is calculated is referred to as radicand. In this expression, √25 = 5, number 25 is the radicand.

Sometimes, you get the complex expressions with multiple radicals and being asked to simplify that.

There are many techniques to do that, depending upon the number of radicals and the values under each radical. We will see them one by one.

How to Simplify Square Roots?

For example, a number 16 has 4 copies of factors, so we take a number two from each pair and put it in front of the radical, finally dropped, i.e., √16 = √(2 x 2 x 2 x 2) = 4.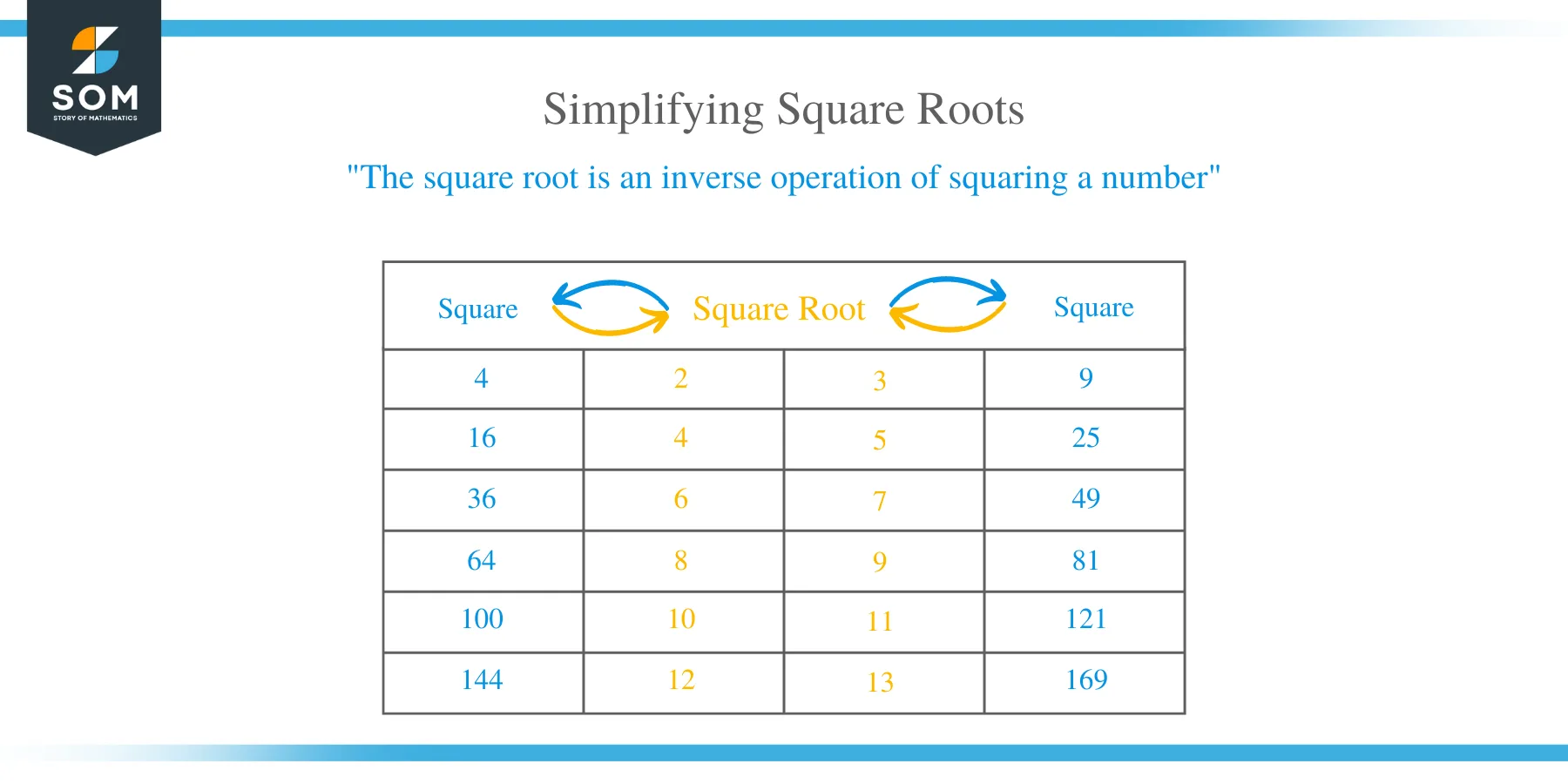

Simplification of the square root of a number entails several methods. This article outlines some of these methods.

Simplification when the Radicals are Alike

You can add or subtract square roots themselves only if the values under the radical sign are equal. Then add or subtract the coefficients (numbers in front of the radical sign) and keep the radical sign’s original number.

Example 1

Perform the following operations

1. 2√3 + 3√3 = (2 +3) √3

= 5√3

1. 4√6 – 2√6 = (4 – 2) √6

= 2√6

• 5√2 + √2 = (5+ 1) √2

= 6√2

Simplification under a single radical sign

You can simplify a square root when the integers are under a single sign by addition, subtraction, and multiplication of the integers under the sign.

Example 2

Simplify the following expressions:

• √(5 x20)

= √100

= 10

• √(30 + 6)

= √36

= 6

• √(30 – 5)

= √25

= 5

• √(3 + 8)

= √11

Simplification when the Radical values are Different

When radicals are not same, simplify the square of a number, by addition or subtraction of different square roots.

Example 3

Perform the following operations:

• √50 + 3√2

= √(25 x 2) + 3√2

= 5√2 + 3√2

= 8√2

• √300 + √12

= √(100 x 3) + √(4 x 3)

= 10√3 + 2√3

= 12√3

Simplifying by Multiplication of Non-negative Roots

Example 4

Multiply:

• √2 x √8 = √16

= 4

• √x ³ + √x ⁵

= √x ⁸ = x ⁴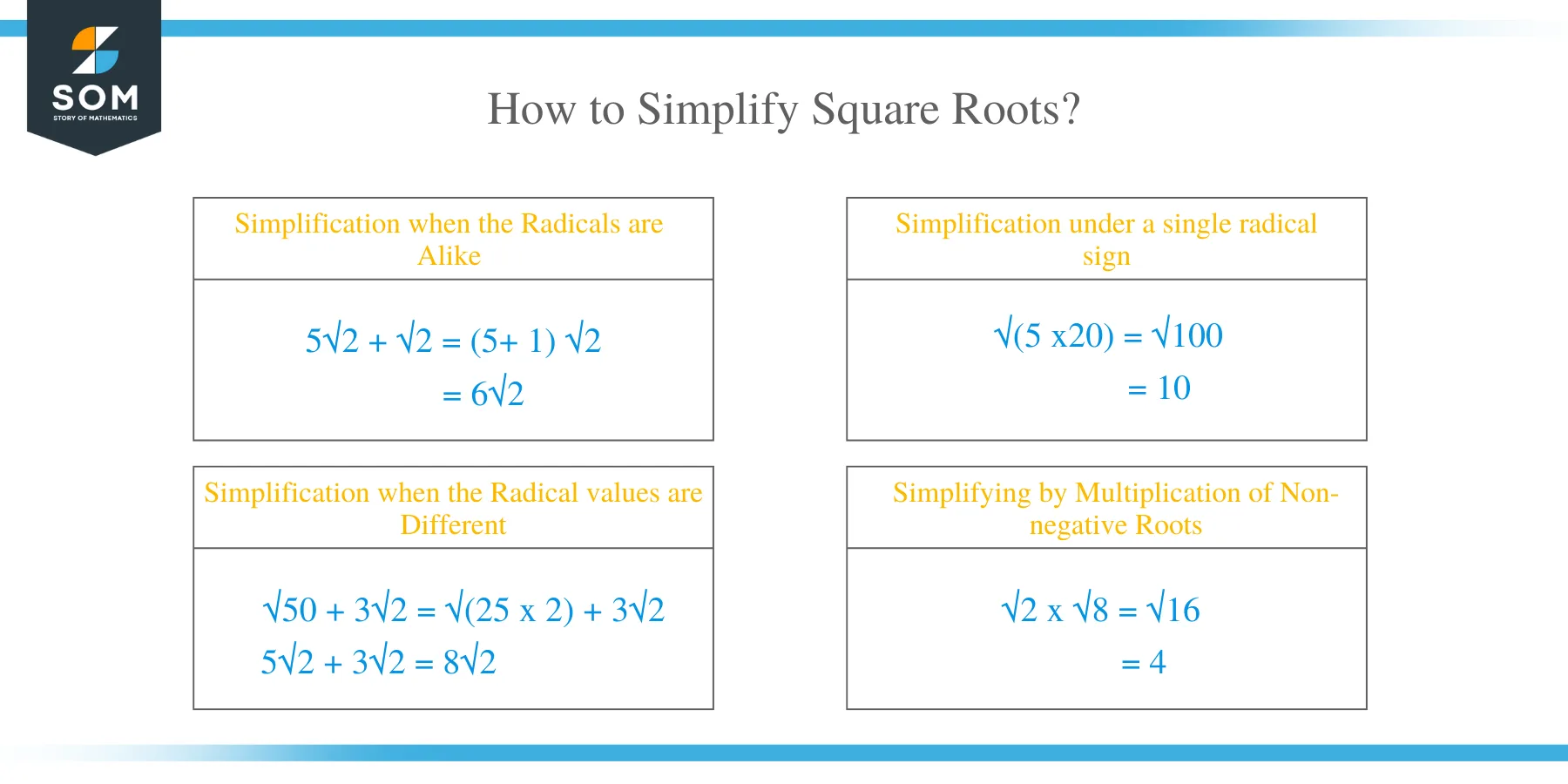

 Example 5

Find the value of a number n if the square root of the sum of the number with 12 is 5.

Solution

Write an expression of this problem, square root of the sum of n and 12 is 5
√(n + 12) = square root of sum.

√(n + 12) = 5
Our equation which should be solved now is:
√(n + 12) = 5
Each side the equation is squared:
[√(n + 12)]² = 5²
[√(n + 12)] x [√(n + 12)] = 25
√[(n + 12) x √(n + 12)] = 25
√(n + 12)² = 25
n + 12 = 25
Subtract 12 from both side of the expression
n + 12 – 12 = 25 – 12
n + 0 = 25 – 12
n = 13

Example 6

Simplify

1. √4,500
2. √72

Solution

The argument 4500 has factors 5, 9, and 100. It is now possible to calculate its square root. Calculate the square root of perfect square numbers

√4500 = √(5 x 9 x 100)

=30√5

2.

Number 72 is equal to 2 x 36, and since 36 is a perfect square, calculate its square root.

√(2 x 36)

= 6√2