- Home
- >
- SSA Triangle – Explanation & Examples
JUMP TO TOPIC
SSA Triangle – Explanation & Examples
We already know how to solve triangles using the first two combinations of sides and angles: SAS triangle and SSS triangle. We have also determined how the Law of Sines, along with these combinations, assures one unique solution and one unique triangle. However, the third combination called SSA triangle is a bit challenging as it may generate multiple solutions. This is the reason SSA is also known as the ambiguous case.
SSA (side-side-angle) triangle is basically a triangular combination when we know the measure of two sides of a triangle and the non-included angle between the sides.
After this topic, we are expected to learn the concepts of the SSA triangle and be able to get answers to these questions.
- What is a SSA triangle?
- How to solve an SSA triangle?
- What is the combinational role of the Law of Cosines and the Law of Sines to solve an SSA triangle?
This lesson also aims to clarify any confusion you may have about the SSA triangles.
What Is a SSA Triangle?
SSA (side-side-angle) triangle is a triangular combination that we get when we know the measure of two sides of a triangle and the non-included angle between the sides.
Consider a triangle $△ABC$ with the sides $a$, $b$, and $c$ facing the angles $\alpha$, $\beta$, and $\gamma$ respectively as shown in Figure 17-1. We can observe that we are given two sides $b$ and $c$, and the non-included angle $\beta$. Figure 17-1 illustrates a triangular combination which is known as an SSA triangle.

SSA and Ambiguous Case
With the SAS and SSS triangle combinations, we get a unique solution for every triangle. However, when we are given two sides and the non-included angle to determine a missing angle — SSA, we may come across the following three conditions.
- No solution (No triangle exists)
- Two solutions (Two different triangles exist)
- One solution (Exactly one triangle exists)
This is why SSA is known as the ambiguous case and we will explain it in detail in the examples below.
How To Solve a SSA Triangle?
We can apply a three-step method to solve an SSA triangle, which includes using the Law of Sines, determining the measure of the third angle, and using the Law of Sines again.
Step 1 of 3
- Use the Law of Sines to measure one of the other two angles
Step 2 of 3
- Determine the measure of the third angle by subtracting the already measured angles (given angle and the angle determined in step 1) from $180^{\circ }$.
Step 3 of 3
- Use the Law of Sines again to measure the missing side.
Important Facts About SSA Triangles and the Law of Sines
Here are some important facts about SSA triangles and the Law of Sines:
- The sine of an angle must be greater than $-1$ and smaller than $+1$. For example, if $\theta$ is the angle, then $-1 < \sin \theta < 1$
- A triangle can never have two obtuse angles
- The sine of an obtuse angle is basically the sine of its supplementary acute angle
Case 1:
No solution (No triangle exists)
Example 1
In triangle $△ABC$, $m∠A = 32^{\circ }$, $a = 14$ and $b = 32$.
What is the measure of angle $B$? Also, determine the total number of distinct triangles that can be drawn.
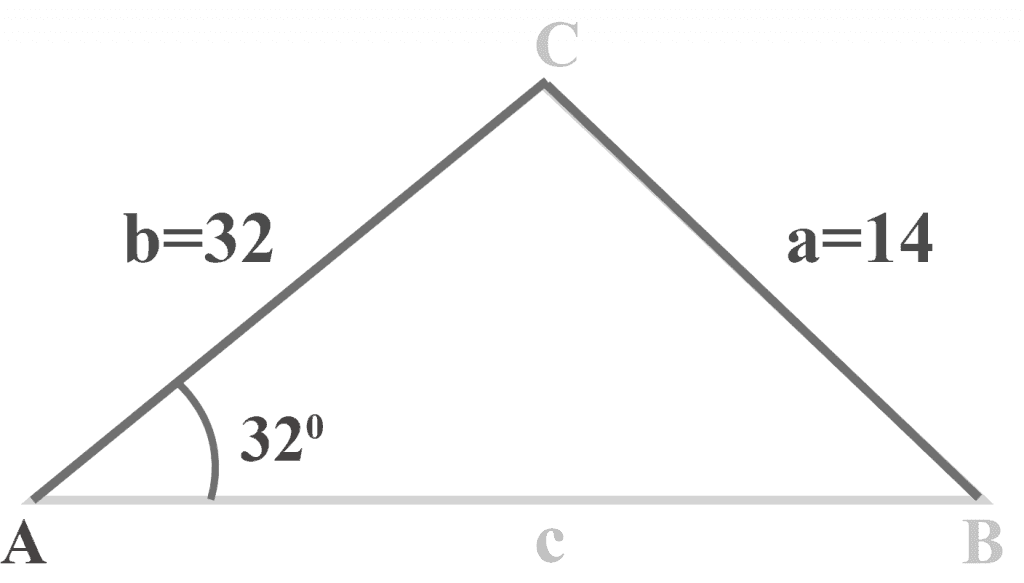
Solution:
Using the Law of Sines
$\frac{\sin\:A\:}{a}=\:\frac{\sin\:B}{b}$
$\frac{\sin\:32^{\circ }\:}{14}=\:\frac{\sin\:B}{32}$
$32 \sin 32^{\circ } = 14 \sin B$
$\sin\:B=32\:\frac{\sin\:32^{\circ }}{14}\:$
$\sin\:B=32\:\frac{0.52991926}{14}\:$
$\sin B = (32) (0.03785138)$
$\sin B = 1.21124403$
It is clear that the sine of angle B is greater than 1, which cannot be possible. So,
$B = \sin^{-1} (1.21124403) =$ ERROR
Note that no triangle exists if $\sin B > 1$.
Reason
Let us draw a perpendicular p from the vertex C and check the situation in terms of a right angle triangle, as shown in the figure below.
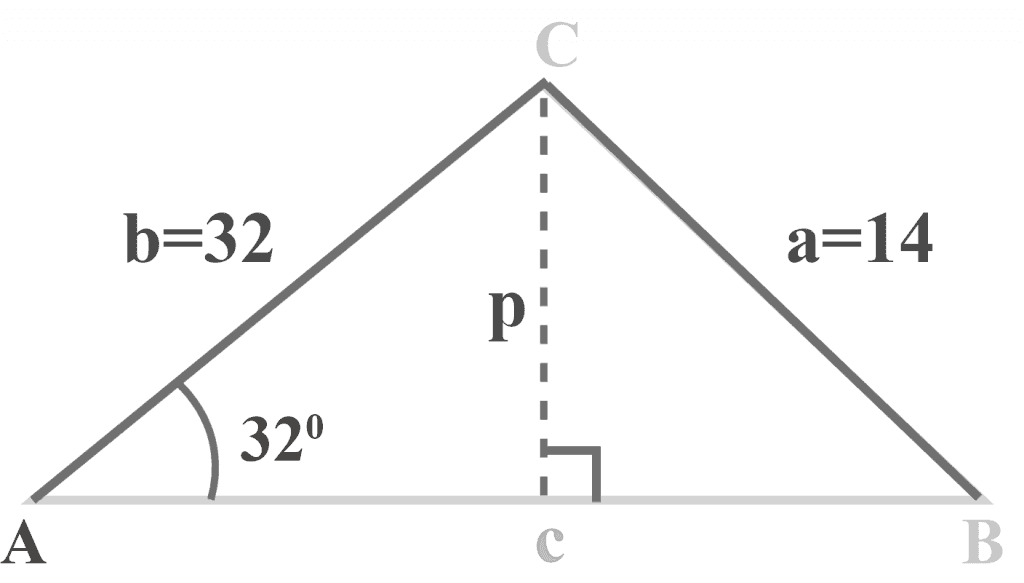
Looking at the figure above, we have
Perpendicular $= p$
Hypotenuse $= b = 32$
$A = 32^{\circ }$
We know that
$\sin A = \frac{perpendicular}{hypotenuse}$
so
$\sin\:32^{\circ }=\frac{p}{32}\:$
$p = (32) (\sin 32^{\circ })$
$p = (32) (0.53991926)$
$p = 19.9574165$
$p ≈ 20$ units
Here
$p > a$
$20 > 14$
Perpendicular > hypotenuse
Since perpendicular cannot be longer than the hypotenuse because the hypotenuse is the longest side in a right-angled triangle, the given triangle is impossible.
Conclusion:
Hence, we conclude that no triangle can exist if
- A is acute and a < p
- A is obtuse and a ≤ b

Case 2:
Two solutions (Two different triangles exist)
Example 2
In triangle $△ABC$, $m∠A = 32^{\circ }$, $a = 22$ and $b = 32$.
What is the measure of angle $B$? Also, determine the total number of distinct triangles that can be drawn.
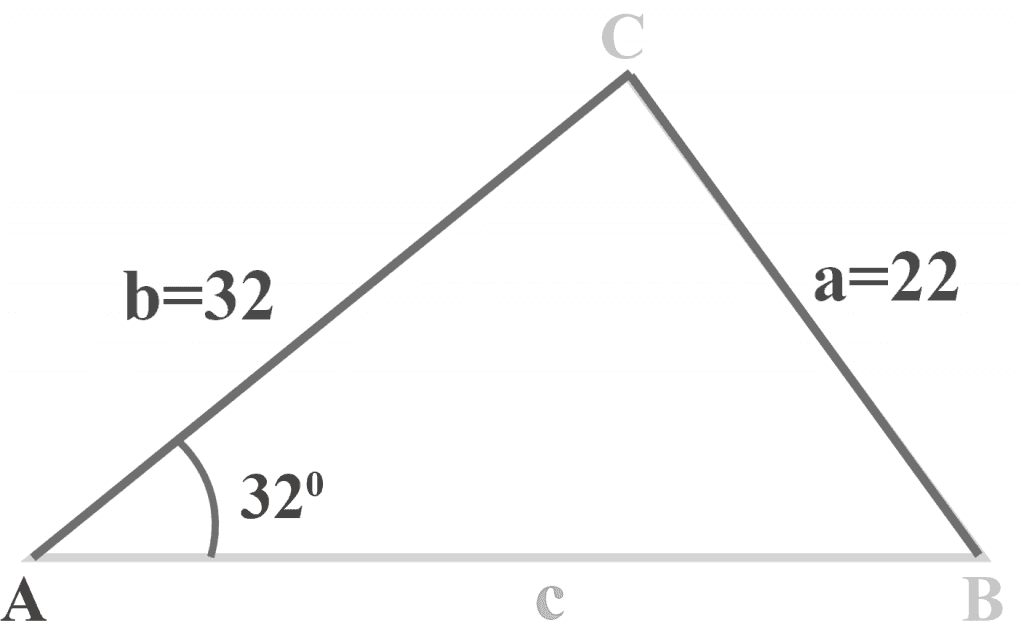
Solution:
Using the Law of Sines
$\frac{\sin\:A\:}{a}=\:\frac{\sin\:B}{b}$
$\frac{\sin\:32^{\circ }\:}{22}=\:\frac{\sin\:B}{32}$
$32 \sin 32^{\circ } = 22 \sin B$
$\sin\:B=32\:\frac{\sin\:32^{\circ }}{22}\:$
$\sin B = (32) (0.02408724)$
$\sin B = 0.77079165$
$B = \sin^{-1} (0.77079165)$
$B ≈ 50.4250317$
$B ≈ 50^{\circ }$
Now, we have
$m∠A = 32^{\circ }$
$m∠B = 50^{\circ }$
so
$m∠C = 180^{\circ } -\: m∠A -\: m∠B$
$m∠C = 180^{\circ } -\: 32^{\circ } -\: 50^{\circ }$
$m∠C = 98^{\circ }$
It sounds OK.
But we stated that the sine of an obtuse angle is basically the sine of its supplement. So $\sin 50^{\circ }$ is also $\sin 130^{\circ }$.
Thus, the triangle could be $m∠B = 130^{\circ }$, $m∠A = 32^{\circ }$ and $m∠C = 18^{\circ }$.
Therefore,
$m∠B = 130^{\circ }$ OR $50^{\circ }$
Two distinct triangles exist, as shown below.
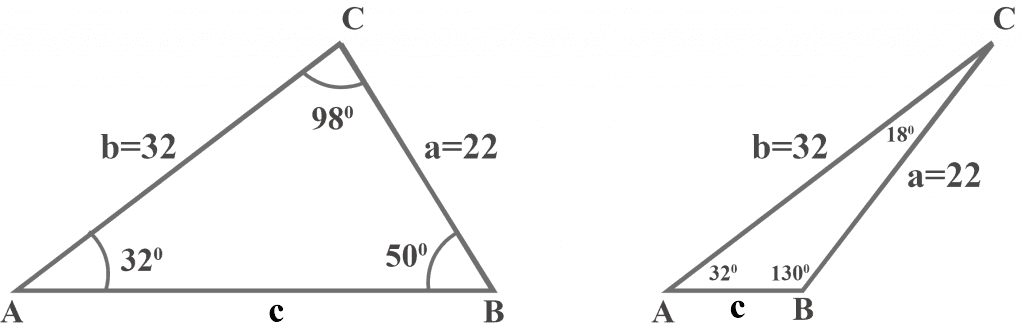
Reason:
We know that the value of $a = 22$, which is larger than the perpendicular $p = 20$, and a triangle will be formed. But, we can also form a second triangle if we swing side $a$ from point C to the left, as shown below.
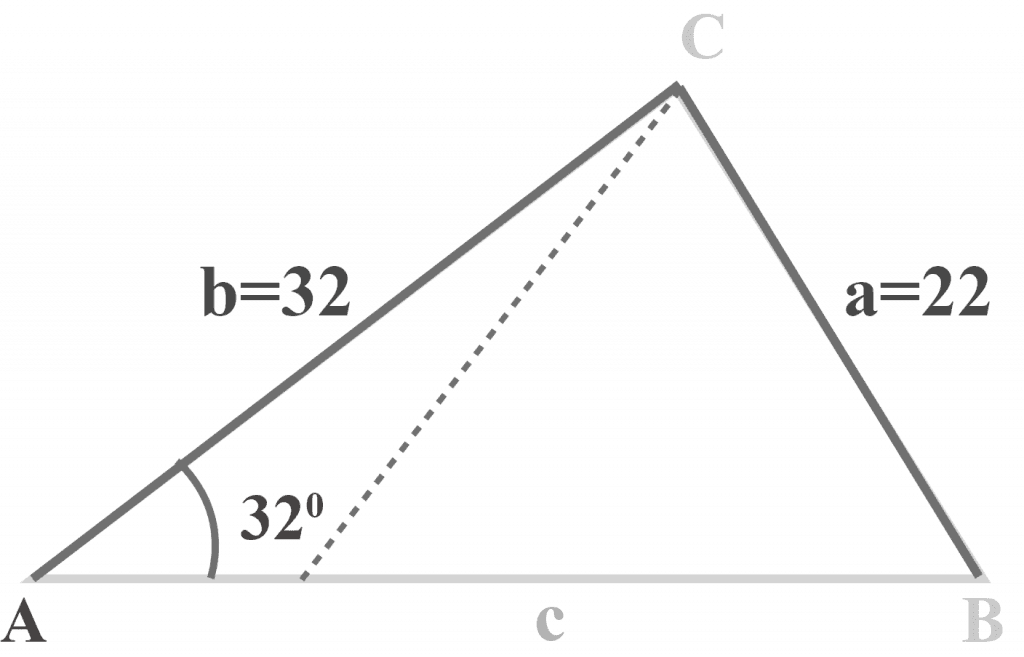
Conclusion:
Hence, we conclude that two triangles can exist if
$p < a < b$
Since a is larger than p, a triangle is formed. But since $a < b$, we can swing it to the left of $p$ and form a 2nd triangle having an obtuse angle, as shown below.
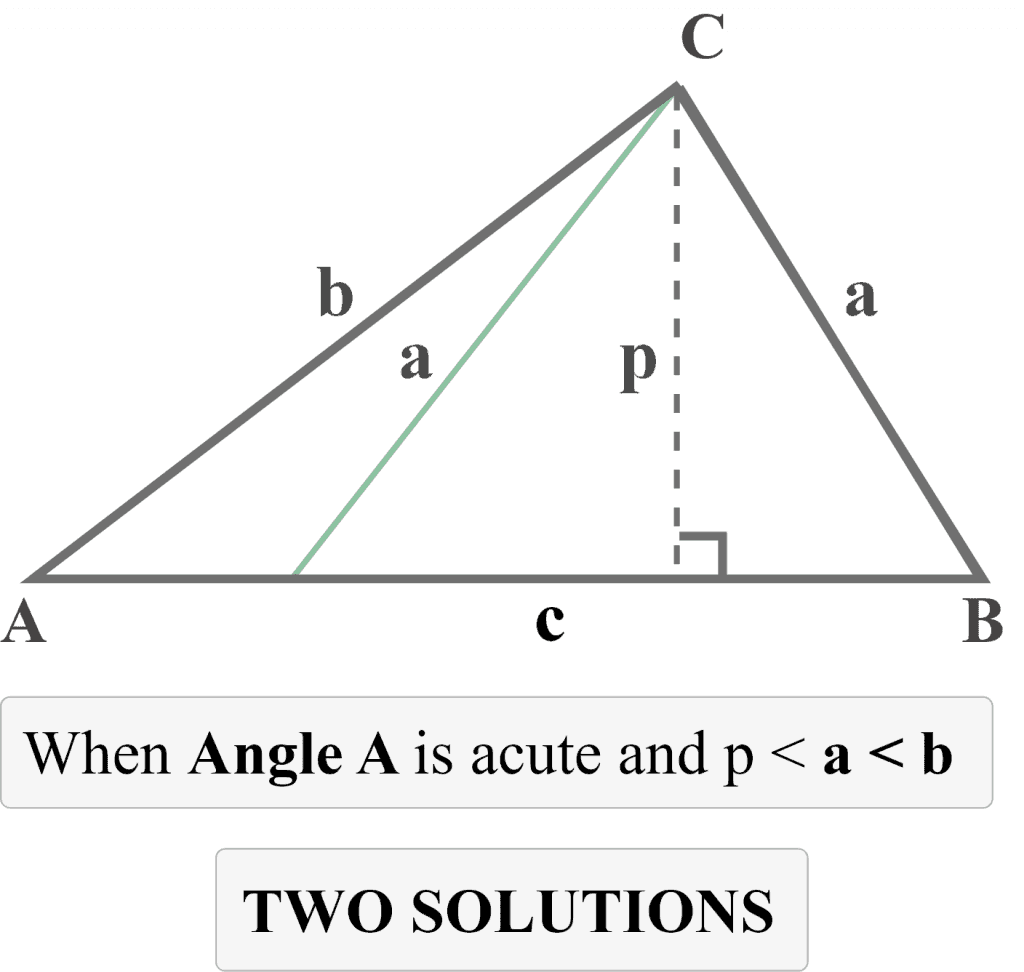
Case 3:
One solution (Exactly one triangle exists)
Example 3
In triangle $△ABC$, $m∠A = 32^{\circ }$, $a = 44$ and $b = 32$.
What is the measure of angle B? Also, determine the total number of distinct triangles that can be drawn.

Solution:
Using the Law of Sines
$\frac{\sin\:A\:}{a}=\:\frac{\sin\:B}{b}$
$\frac{\sin\:32^{\circ }\:}{44}=\:\frac{\sin\:B}{32}$
$32 \sin 32^{\circ } = 44 \sin B$
$\sin\:B=32\:\frac{\sin\:32^{\circ }}{44}\:$
$\sin\:B=32\:\frac{0.52991926}{44}\:$
$\sin B = (32) (0.01204362)$
$\sin B = 0.38539583$
$B = \sin^{-1} (0.38539583)$
$B ≈ 22.6683158$
$B ≈ 23^{\circ }$
As the supplement of $23^{\circ }$ is $157^{\circ }$. But,
$157^{\circ } + 35^{\circ } > 189^{\circ }$
Therefore,
$m∠B = 23^{\circ }$
Hence, ONE distinct triangle exists.
Conclusion:
Hence, we conclude that ONE triangle exists if
- A is acute and $a > b > p$
- A is obtuse and $a > b$
- A is acute and $a = p$
The following diagram illustrates these cases.

