SSS Triangle – Explanation & Examples

How do we solve for the unknown parts of a triangle when we only know the measure of all its three sides? It’s pretty simple. We will use the SSS (side-side-side) triangle combination to find the angles. 

SSS (side-side-side) triangle is basically a triangular combination when we know the measure of three sides of a triangle and need to determine the remaining parts (angles) of a triangle.

After studying this lesson, we are expected to learn the concepts driven by the following questions and be able to address them.

• What is a SSS triangle?
• How to solve a SSS triangle?
• What is the combinational role of the Law of Cosines and the Law of Sines to solve a SSS triangle?

It is also the goal of this lesson to clear up any confusions you might have about the concept of SSS triangles. Let’s begin. 

What Is a SSS Triangle?

SSS (side-side-side) triangle is a triangular combination that we get when we know the measure of three sides of a triangle and need to determine the remaining parts (angles) of a triangle.

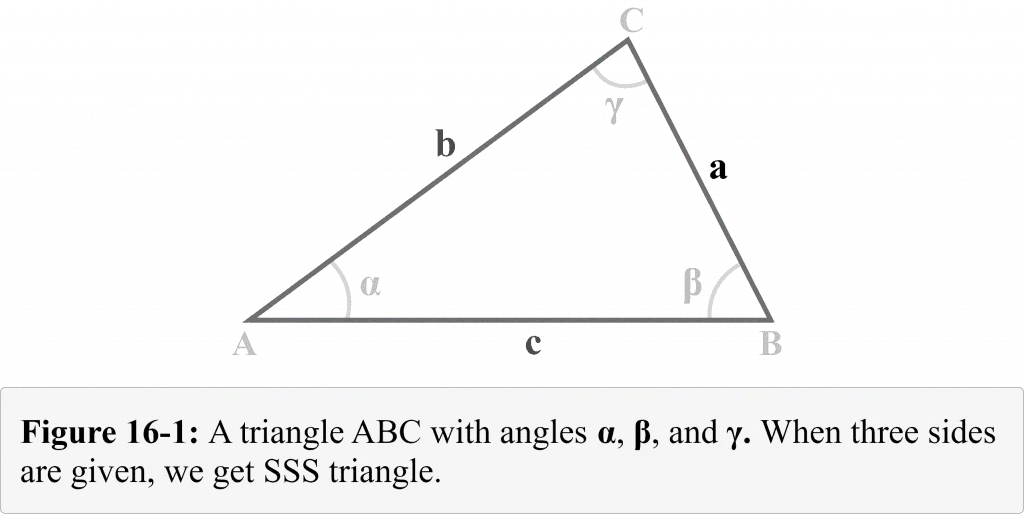
Consider a triangle $△ABC$ with the sides $a$, $b$, and $c$ facing the angles $\alpha$, $\beta$, and $\gamma$ respectively as shown in Figure 16-1. We can observe that we are given the three sides $a$, $b$, and $c$. Therefore, the below Figure 16-1 illustrates a triangular combination which is known as a SSS triangle.

How To Solve a SSS Triangle

When we know the measure of three sides of a triangle, we can apply three-step methods to solve a SSS triangle: using the Law of Cosines, using the Law of Sines, and determining the measure of the third angle.

Step 1 of 3

• Use the Law of Cosines to measure the largest angle — an angle opposite the longest side.

Step 2 of 3

• Use the Law of Sines to determine either of the remaining acute angles.

Step 3 of 3

• Determine the measure of the third angle by subtracting the already measured angles in the previous steps from $180^{\circ }$.

Example 1

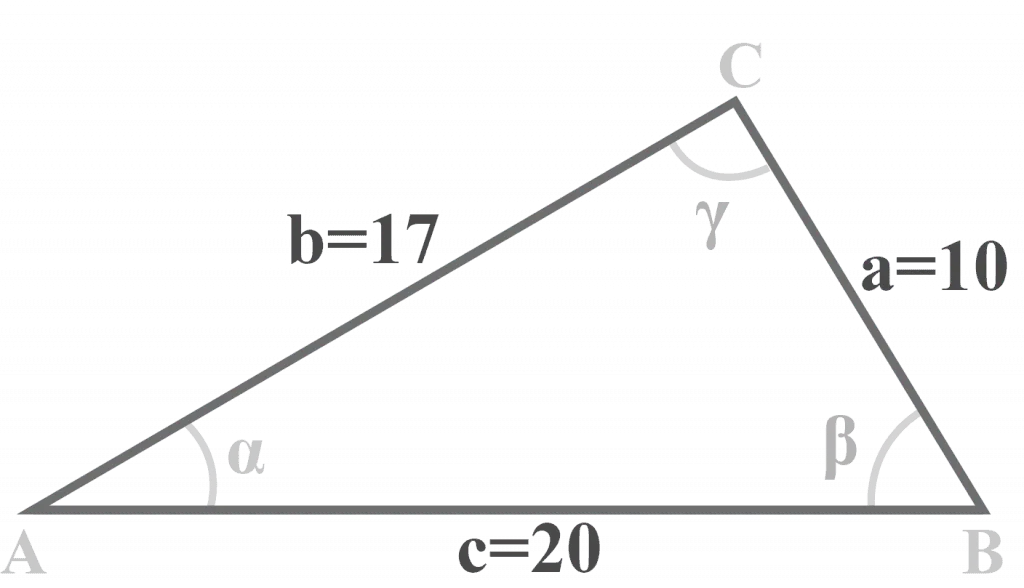
In triangle $△ABC$, $a = 10$, $b = 17$ and $c = 20$ cm. Solve the triangle.

Solution:

We are given three sides $a = 10$, $b = 17$, and $c = 20$. Thus, we will apply the three-step method to solve a SSS triangle.

Step 1 of 3

Use the Law of Cosines to measure the largest angle — an angle opposite the longest side.

The angle $\gamma$ is opposite the longest side $c = 20$. Thus, we need to find the angle $\gamma$.

Applying the law of cosines

$c^2\:=\:a^2\:+b^2\:-\:2ab\:\cos\:\gamma$

$\cos\:\gamma=\frac{\left(a^2\:+\:b^2\:-\:c^2\right)}{2ab}$

substituting $a = 10$, $b = 17$ and $c = 20$ in the formula

$\cos\:\gamma=\frac{\left(10^2\:+\:17^2\:-\:20^2\right)}{2\:(10)\:(17)}$

$\cos\:\gamma=\frac{\left(100\:+\:289\:-\:400\right)}{340}$

$\cos\:\gamma=-\frac{11}{340}$

$\gamma = \cos^{-1} (-0.0324)$

$\gamma = 91.857…^{\circ }$

$\gamma ≈ 92^{\circ }$ (angle to the nearest degree)

Step 2 of 3

Use the Law of Sines to determine either of the remaining acute angles.

Now it is very straightforward to determine the angle $\alpha$.

Applying the law of sines

$\frac{a}{\sin\:\alpha\:}=\:\frac{c}{\sin\:\gamma}$

$\sin\:\alpha=a\:\frac{\sin\:\gamma}{c}$

substituting $a = 10$, $c = 20$ and $\gamma = 91.857^{\circ }$

Please note that it is recommended to use the unrounded value of angle $\gamma = 91.857^{\circ }$ because the angle $\gamma = 92$ is rounded to the nearest degree.

$\sin\:\alpha=10\:\frac{\sin\:91.857^{\circ }}{20}$

$\sin\:\alpha=10\:\frac{0.999}{20}$

$\sin\:\alpha = 10 (0.04995)$

$\sin\:\alpha = 0.4995$

$\alpha = \sin^{-1} (0.4995)$

$\alpha = 29.967…^{\circ }$

$\alpha ≈ 30^{\circ }$ (angle to the nearest degree)

Step 3 of 3

Determine the measure of the third angle by subtracting the already measured angles in the previous steps from 180º.

$\beta = 180^{\circ }\: – \alpha\: – \gamma$

substituting $\alpha = 30^{\circ }$ and $\gamma = 92^{\circ }$

$\beta= 180^{\circ }\: -\: 30^{\circ }\: –\: 92^{\circ }$

$\beta = 58^{\circ }$

Thus, the solution for the given SSS triangle is:

$\alpha = 30^{\circ }$, $\beta = 58^{\circ }$ and $\gamma = 92^{\circ }$

Determining the Largest Angle

If we know the cosine of an angle, we can easily determine whether the angle is acute or obtuse depending upon the following conditions:

The condition for the acute Angle

$\cos \theta  > 0%%EDITORCONTENT%%nbsp;      for        $0^{\circ } < \theta  < 90^{\circ }$  

The condition for the obtuse Angle

$\cos \theta < 0%%EDITORCONTENT%%nbsp;       for         $90^{\circ } < \theta < 180^{\circ }$

Since the $\gamma ≈ 92^{\circ }$ was obtuse, we already figured out that the angles $\alpha$ and $\beta$ must be acute. This is the reason a single triangle cannot have multiple obtuse angles.

It is also very important to remember that if the largest angle is acute, then the remaining two angles would also be acute.

Example 2

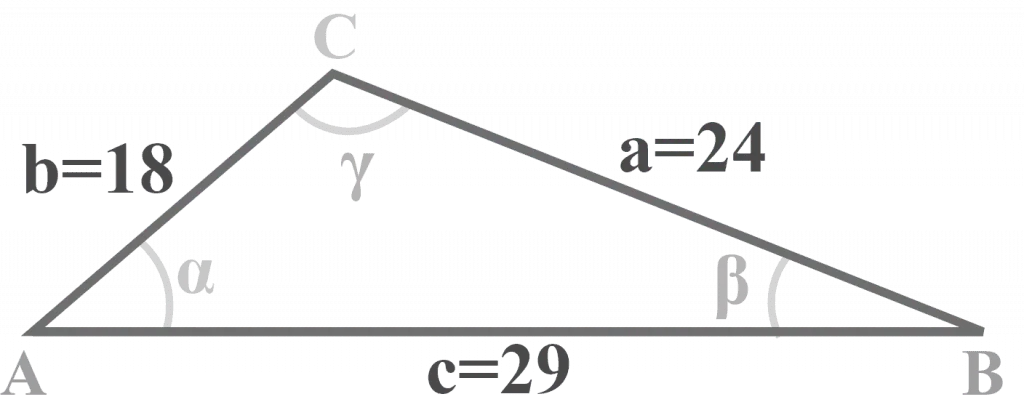
In triangle $△ABC$, $a = 24$, $b = 18$ and $c = 29$ cm. Solve the triangle.

Solution:

We are given three sides $a = 24$, $b = 18$, and $c = 29$. Thus, we will apply the three-step method to solve a SSS triangle.

Step 1 of 3

The angle $\gamma$ is opposite the longest side $c = 29$. Thus, we need to find the $\gamma$.

Applying the law of cosines

$c^2\:=\:a^2\:+b^2\:-\:2ab\:\cos\:\gamma$

$\cos\:\gamma=\frac{\left(a^2\:+\:b^2\:-\:c^2\right)}{2ab}$

substituting $a = 24$, $b = 18$ and $c = 29$ in the formula

$\cos\:\gamma=\frac{\left(24^2\:+\:18^2\:-\:29^2\right)}{2\:(24)\:(18)}$

$\cos\:\gamma=\frac{\left(576\:+\:324\:-\:841\right)}{864}$

$\cos\:\gamma=\frac{59}{864}$

$\gamma = \cos^{-1} (0.0682)$

$\gamma = 86.084…^{\circ }$

$\gamma ≈ 86^{\circ }$ (angle to the nearest degree)

Step 2 of 3

Now it is very straightforward to determine angle. Thus, we will determine the angle $\beta$.

Applying the law of sines

$\frac{a}{\sin\:\alpha\:}=\:\frac{c}{\sin\:\gamma}$

$\sin\:\beta=b\:\frac{\sin\:\gamma}{c}$

substituting $b = 18$, $c = 29$ and $\gamma = 86.084^{\circ }$

$\sin\:\beta=18\:\frac{\sin\:86.084^{\circ }}{29}$

$\sin\:\beta=18\:\frac{0.998}{29}$

$\sin\:\beta = 18 (0.03441)$

$\sin\:\beta = 0.61938$

$\beta = \sin^{-1} (0.61938)$

$\beta = 38.271…^{\circ }$

$\beta ≈ 38^{\circ }$ (angle to the nearest degree)

Step 3 of 3

Subtract $m∠\beta = 38^{\circ }$ and $m∠\beta = 86^{\circ } from $180^{\circ }$.

$\alpha = 180^{\circ }\: – \beta\: – \gamma$

$\alpha = 180^{\circ }\: -\: 38^{\circ }\: –\: 86^{\circ }$

$\beta = 56^{\circ }$

Thus, the solution of the given SSS triangle is:

$\alpha = 56^{\circ }$, $\beta = 38^{\circ }$ and $\gamma = 86^{\circ }$

Example 3

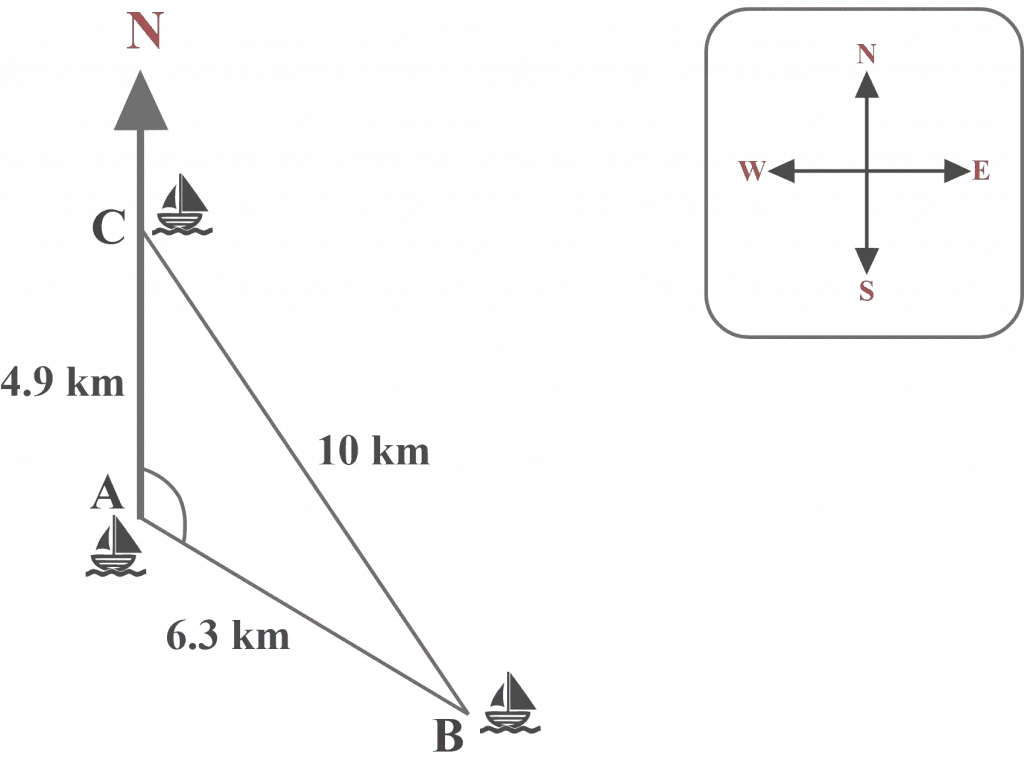
The following diagram illustrates three ships $A$, $B$ and $C$ and the distance between them. Determine the bearing of ship $B$ from ship $A$.

Solution:

Looking at the diagram, it is clear that the triangle $△ABC$ represents a SSS case as we have:

$a = 10$, $b = 4.9$ and $c = 6.3$

We need to determine the angle $A$ to find the bearing of ship $B$ from ship $A$.

Applying the law of cosines

$a^2\:=\:b^2\:+c^2\:-\:2bc\:\cos\:A$

$\cos\:A=\frac{\left(b^2\:+\:c^2\:-\:a^2\right)}{2bc}$

substituting $a = 10$, $b = 4.9$ and $c = 6.3$ in the formula

$\cos\:A=\frac{\left(4.9^2\:+\:6.3^2\:-\:10^2\right)}{2\:(4.9)\:(6.3)}$

$\cos\:A=\frac{\left(24.01\:+\:36.69\:-\:100\right)}{61.74}$

$\cos\:A=\frac{-36.3}{61.74}$

$\cos\:A=-0.5879$

$A = \cos^{-1} (-0.5879)$

$A = -0.5879…^{\circ }$

$A = 126.008…^{\circ }$

$A ≈ 126^{\circ }$ (angle to the nearest degree)

Therefore, the bearing of ship $B$ from ship $A$ is $126^{\circ }$.