Subsets – Definition and Examples

In our previous discussion, we learned that a set is a collection of distinct elements. So, what happens if we take out some elements from this collection and form a subgroup. Is this subgroup meaningful? Will it have any unique properties? What can we call it? These questions can all be answered by the concept of Subsets. 

This article will try to address these questions individually, so let’s get going.

The division of a set leads to the formation of smaller sets called subsets.

The topics we will cover in this article are:

• What is a subset?
• How to represent a subset?
• Properties of a subset
• Examples
• Practice Problems

What is a subset?

A subset, as the name suggests, is a subcollection of any set. Let us assume we have two sets, X and Y. Mathematically speaking, X will be a subset of Y if and only if all the elements of X are present in Y. We can also say that X is contained in Y. This relationship is called inclusion or containment of X in Y. 

To understand it more, consider you have a set A such that A includes the names of all the cities in your country. In that case, a set B comprising the names of cities in your province will be a subset of A. This is because all the cities in your province must also be cities of your country; therefore, B is a subset of A.

There are only a certain number of distinct or unique subsets for any set, so the rest are redundant and repetitive. 

A subset can be classified as follows:

1. Proper subset
2. Improper subset

Let’s solve some examples of a subset:

Example 1

Determine whether A is a subset of B in the following:

1. A = {set of all even numbers}, B = {set of whole numbers}
2. A = {1, 2, 3}, B = {1, 2, 3, 4, 5, 6, 7, 8, 9}
3. A = {all writing equipment at a stationary shop}, B = {pens}
4. A = {sedan}, B = {all cars}

Solution

(i) The set of even numbers is given as:

     A = {0, 2, 4, 6, …}

    Similarly, the set of whole numbers is given as:

B = {0, 1, 2, 3, …}

      It is quite clear that the elements of A belong to set B. So A is a subset of B

(ii) It is clear from analyzing the two sets A and B that A’s elements belong to set B. So A is a subset of B

(iii) Set A includes pens, pencils, notepads, markers, etc. Whereas set B only includes pens. So we cannot say that all A’s elements are in B, which is a condition for A to be a subset of B. In this case, B is a subset of A, but A is not a subset of B.

(iv) Set B includes all types of cars; sedans, hatchbacks, pickup trucks, etc. And, A is a set of sedans. So all elements of A are included in B. Therefore, A is a subset of B.

Types of subsets

Earlier, we mentioned that there are two types of subsets. So what are these types? Let’s have an overview.  

Proper subset

Any set A is considered a proper subset of B if there is at least one element in B, which is not present in A.

In other words, if A and B are unequal and all elements of A are present in B, then A is the proper subset of B. 

It is also called a strict subset. 

Let’s do an example:

Example 2

1. Is A a proper subset of B when A = {1, 2, 3, 8} and B = {1, 2, 3, 8}?
2. Is A a proper subset of B when A = {1, 2} and B = {1, 5, 6, 7}?

Solution

1. No, A is not a proper subset of B as both are equal, and B has no unique element, which is not present in A.
2. No, A is not a proper subset. It is not even a subset as 2 is not present in B.

Improper Subset

Consider two sets, A and B; A is an improper subset of B if it contains all the elements of B. Any set is an improper subset of itself. 

How to Represent Subsets?

We have familiarized ourselves with what a subset is, now let’s see how to represent it. A subset, like any other set, is written with its elements inside curly brackets. But its representation is a different matter. As a subset is a part of a set, so it is written using an intuitive symbol ⊆ which is read as ‘is a subset of’:

So, consider two sets, A and B: 

If A is a subset of B, then we write it as:

A ⊆ B

If A is not a subset of B, we write it as:

A ⊈ B

Some mathematicians also use the symbol ⊂ to denote a proper subset. So, we can also write the above statements as follows:

If A is a proper subset of B, then we represent it as:

 A ⊂ B. 

If A is not a proper subset of B, then we write it as:

 A ⊄ B

To understand the difference between ⊆ and ⊂, we can think of the inequality signs ≤ and <. For any two numbers a and b, if a ≤ b, then a may or may not be equal to b. On the contrary, if we have a < b, then a is smaller than b. 

The symbols  ⊆  and ⊂ are similar; for A ⊆ B, A may be equal to B, but for A ⊂ B, A is never equal to B; hence, it is a proper subset.

Difference between Proper Subset and Superset

A common cause of confusion among students studying set theory for the first time is the difference between a proper subset and a superset. So let’s try to address this confusion. 

As discussed earlier, A is a proper subset of B if B has at least one element not present in A. It is denoted by the symbol ‘⊂,’ which expresses that A is a proper subset of B. It is also called a strict subset. 

Whereas B will be the superset of A if and only if all the elements present in A are a part of B, which loosely translates to B being greater in size than A. If A is the proper subset of B, then B is the superset of A. The symbol used to denote a superset relationship is ‘⊇.’

The following example can help us understand this better.

Example 3

Explain why A = {2, 4, 5, 7, 8} is a superset of B = {2, 4, 5}.

Solution

For A to be a superset of B, it needs to have all the elements present in set B. As we can see from the given information, A has elements equal to B, whereas B is a proper subset of A; therefore, A is B’s superset. 

It is written as:

A ⊇ B

Representation of Subsets through Venn Diagrams

To understand the relationships between different sets, the Venn diagram is the most suitable tool to visualize logical connections between certain sets. They are used abundantly for the representation of sets, more importantly, finite sets. A Venn diagram denotes the sets as regions inside a circular object with the elements as points inside the region. 

As subsets usually include two sets, we can easily use a Venn diagram to explain and visualize them. The figure is as follows:

Consider we have set A = {1, 5, 9} and set B = {1, 5, 9, 12, 15, 2, 3}. 

The Venn diagram representation of sets A and B are as follows:

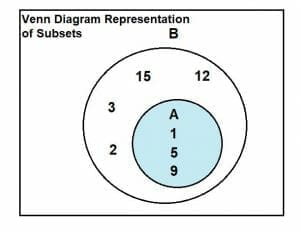
As we can observe from diagram A, enclosed by a region denoted by its set, is a part of region B. Each region has its elements denoted as points inside the region.

Let’s solve another example using the Venn diagram.

Example 4

With the help of Venn Diagram, show that B = {1, 5, 9, 12, 15, 2, 3} is a superset of A = {1, 5, 9}.

Solution

As B will be a superset of A when all its present elements are a subgroup of B elements, we have to solve it using the Venn Diagram.

The Venn diagram is as follows:

As we can see that there is an entirely overlapping region of A and B with some region of B to spare, so B is a superset of A.

Properties of Subsets

Subsets are one of the most fundamental concepts in the realm of sets. Emphasizing the importance of subsets, it is necessary to evaluate the properties of subsets. Following are some of the most vital properties of subsets.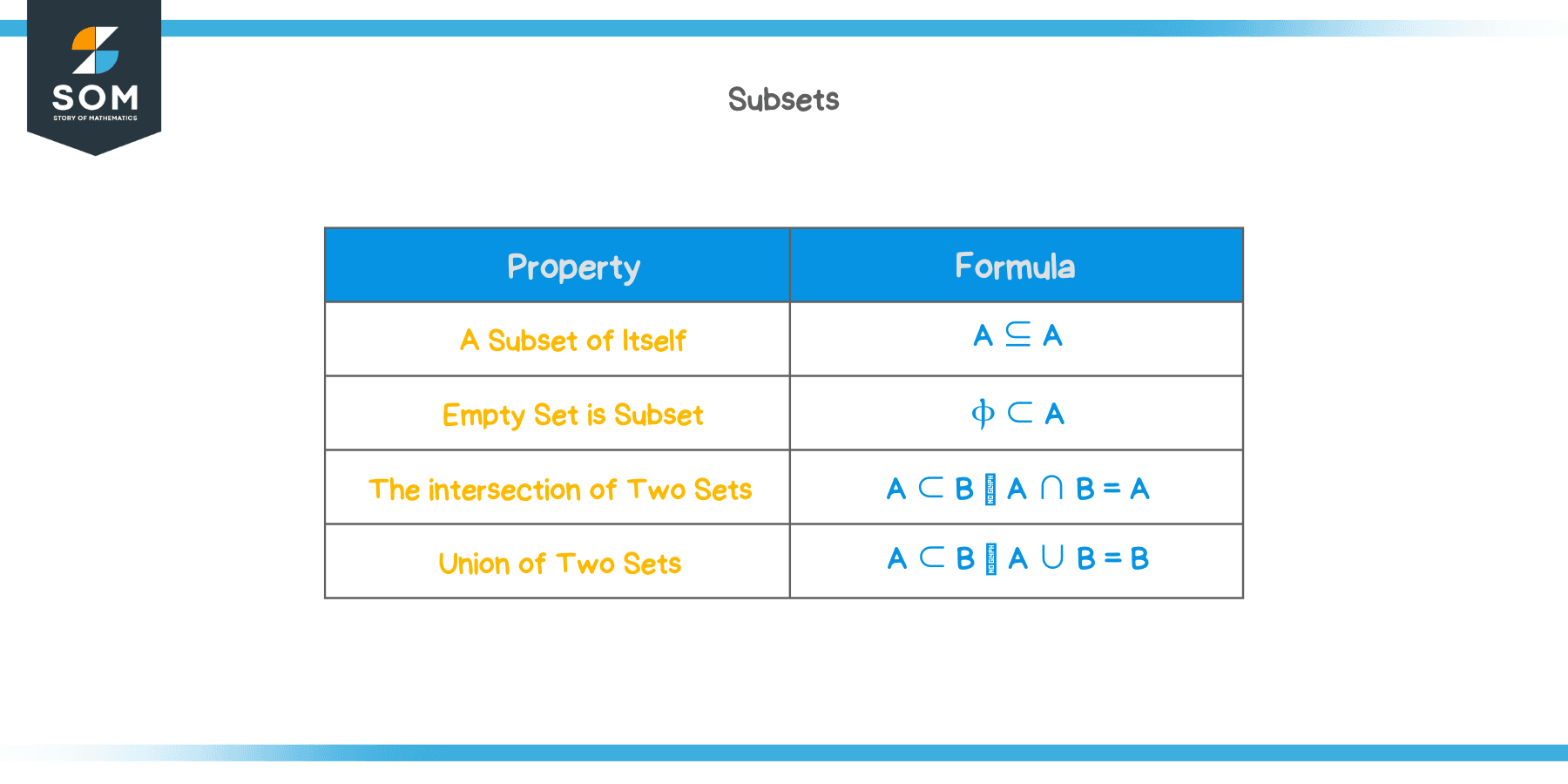

A Subset of Itself:

Every set is considered to be a subset of itself.

Either we have a finite or an infinite set, a set itself will be considered the subset of itself. This happens unconditionally. Whenever we’re listing down the subsets of any given set, we will always include the set itself as its subset. 

But in the case of proper subsets, we will skip the set itself to make the subset equal to the set.

For example, for a finite set A = {2,5}, all the possible subsets are:

 A = Ⲫ, A = {2}, A = {5}, A = {5}, A = {2, 5}

As you can see, we have included a subset with the same elements as the original set to satisfy the property.

As mentioned before, this is not only for finite sets; infinite sets follow the same property. 

Empty Set is Subset:

The empty set is the subset of every set.

Let’s say we consider a set A, which can be finite or infinite. We can calculate all the possible subsets of A; among these subsets, we will include a null/empty set. 

For example, consider a finite set A = {1, 2}, so all the possible subsets of this set are:

A = Ⲫ, A = {1}, A = {2}, A = {1, 2}

As you can see, we have included a subset that is empty among our list of subsets to satisfy the property:

Ⲫ ⊂ A

In the case of infinite sets, we can apply the same principle. It does not matter whether a set is finite or infinite; an empty set will always be a subset of the given set. 

Let’s look at an example to apply this better.

Example 5

Consider a set X = {2, 5, 8}. List all its possible subsets.

Solution

To solve this example, we will consider the above property. 

The list of all the subsets of set X is:

Ⲫ, {2}, {5}, {8}, {2, 5}, {5, 8}, {2, 8}

An empty set is also a subset because of the following relation:

Ⲫ ⊂ X

The intersection of Two Sets

Set A will be the subset of set B if and only if A and B’s intersection is equal to A. 

For a given finite or infinite set A, for it to be a subset of any finite/infinite set B, their intersection must always be equal to set A. This is one of the conditions for set A to be a subset of set B. If this condition fails to hold, then we can easily say that set A is not the subset of set B.

We can denote this as:

A ⊂ B 🡪 A ∩ B = A

Let’s look at an example to apply this better.

Example 6 

Consider a set X = {2, 5, 8} and Y = {2, 4, 5, 6, 7, 8}. Is X a subset of Y?

Solution

To solve this example, we will consider the above property. 

X∩Y = {2, 5, 8}

As this is equal to X, therefore, X is a subset of Y.

Union of Two Sets:

For any set A to be the subset of set B, their union must be equal to set B.

For a given finite or infinite set A, for it to be a subset of any finite/infinite set B, their union must always be equal to set B. This is one of the conditions for set A to be a subset of set B. If this condition fails to hold, then we can easily say that set A is not the subset of set B.

We can denote this as:

A ⊂ B 🡪 A ∪ B = B

Let’s look at an example to apply this better

Example 7

Consider a set X = {2, 8} and Y = {2, 6, 7, 8}. Is X a subset of Y?

Solution

To solve this example, we will consider the above property. 

X ∪ Y = {2, 6, 7, 8}

As their union is equal to Y, therefore, X is a subset of Y.

Calculating the Number of Proper Subsets and Subsets:

For a set with n number of elements, using the following formula, we can calculate the number of subsets:

$2^n&

And using this formula, we can calculate the number of proper subsets:

$2^n – 1$

Practice Problems

1. Give a real-life example of the proper subset.
2. Find the number of proper subsets for the given set A = {1, 6, 2, 4, 5}.
3. For the given set A = {2, 4, 6, 8, 9}, find the number of subsets containing 2 elements.
4. What is the relationship between A = {b, q, u, j} and B={x : x is any letter}?
5. What is the relationship between A = {x : x is negative even number} and B = {x 😡 is Natural number}.

Answers:

2. 31
3. 10
4. proper subset
5. Not a subset

Previous Lesson | Main Page | Next Lesson