Subtracting Complex Numbers – Techniques, Explanation, and Examples

If we can subtract real numbers, it makes sense that we can also subtract complex numbers. Subtracting complex numbers will also help us review what we’ve learned about subtracting two binomials.When subtracting complex numbers, we simply subtract the real number parts and subtract the imaginary number parts.Remember when we combine like terms when subtracting binomials? We’ll apply a similar process when subtracting two complex numbers.

How to subtract complex numbers?

The general form of a complex number is of the form $a + bi$. If we have another complex number, $m + ni$, we can find the difference between the two by following the steps below:

Distribute the negative sign inside the parenthesis.
Group the real number and the imaginary number parts.
Simplify each group by adding or subtracting the coefficients.

Let’s following these steps to find the difference between $a + bi$ and $m + ni$.$\begin{aligned} (a + bi) – (m + ni) &= a + bi -m – ni \color{green}\text{ Distributive the negative sign}\\&= (a – m) + (bi – ni) \color{green}\text{ Group the real and imaginary parts}\\&= (a – m) + (b -n)i \color{green}\text{ Simplify the terms}\end{aligned}$This means that the general form of the difference between the two complex numbers, $a + bi$ and $m + ni$, is equal to $(a – m) + (b – n)i$.

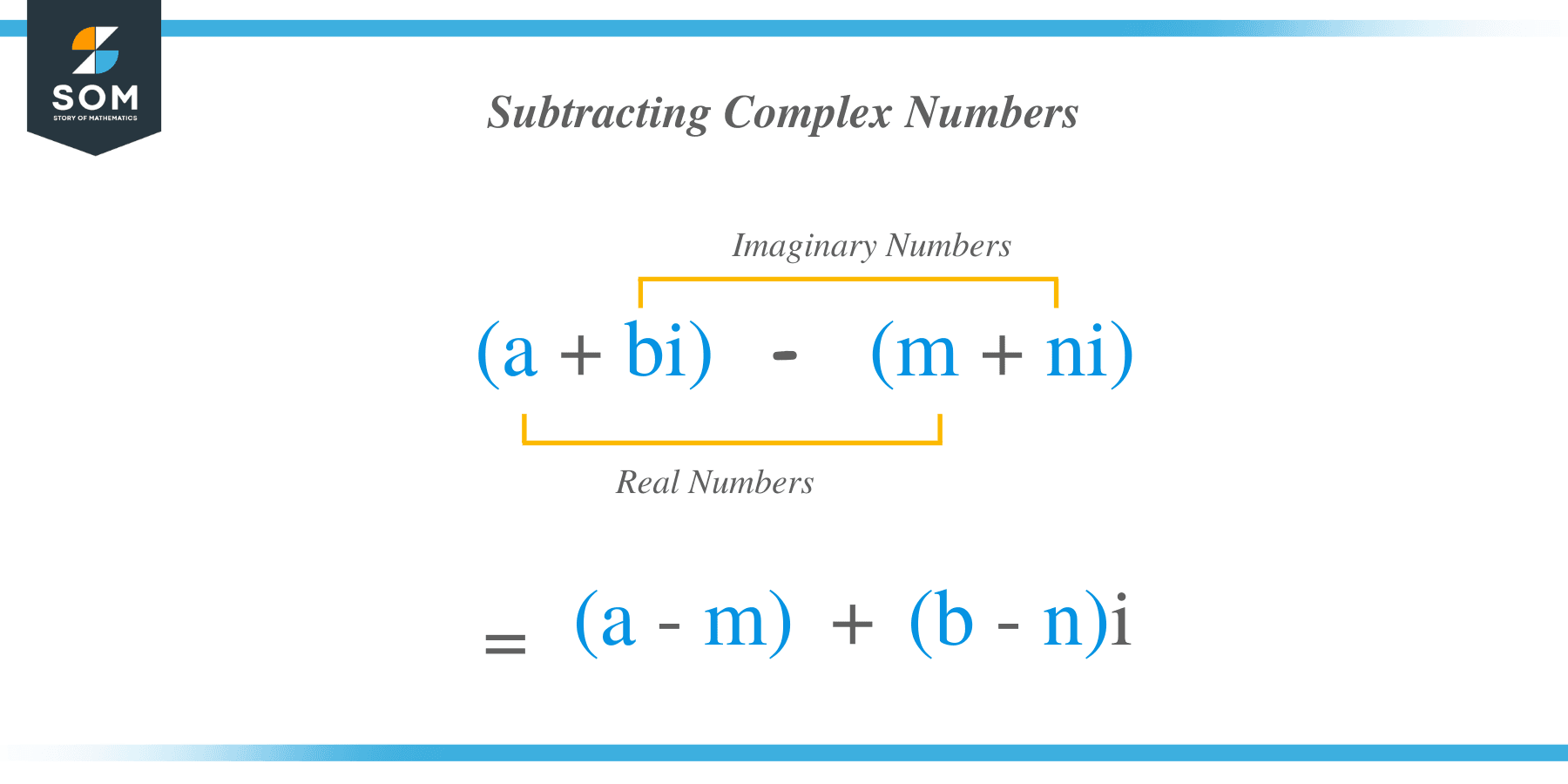
Examples of complex number subtraction

The degree of difficulty when subtracting complex numbers may vary, so we’ll show some common cases you may encounter.Case 1: Subtracting a complex number from a real numberLet’s say we have the real number, $m$. We can subtract $a + bi$ from it by distributing the negative sign before the parenthesis correctly.$ \begin{aligned} m – (a + bi) &= m – 1(a) – 1(bi)\\&= m – a – bi\end{aligned}$We can apply a similar process whenever we want to subtract a complex number from the given real number.Case 2: Subtracting a complex number from an imaginary numberLet’s say we have an imaginary number, $ni$. We can subtract $a + bi$ from it by:

Distributing the negative sign correctly into the parenthesis.
Combine the two imaginary numbers.

$ \begin{aligned} ni – (a + bi) &= ni – 1(a) – 1(bi)\\&= – a + (ni – bi)\\&= -a + (n – b)i\end{aligned}$This process applies whenever we want to subtract a complex number from an imaginary number. We’ll also apply a similar process if we want to subtract an imaginary number from a complex number, but the signs will change.Case 3: Subtracting a complex number from another complex numberWe’ve discussed this case already in the earlier section because this covers the general form of complex numbers.If we want to subtract $m + ni$ from $a + bi$, is equal to $(a – m) + (b – n)i$. The order of the two matters since subtraction is not commutative.Remember that when we’re asked to subtract “$a$ from $b$,” we want to find $b – a$. In the same way that if we want to “subtract $b$ from $a$,” we’re looking for $a – b$.

Example 1

What is the result when $-8$ is subtracted from $-5 + 6i$? SolutionWe want to find the difference between $-5 + 6i$ and $-8$. Make sure to distribute the negative sign correctly. Combine the real number of parts to simplify the result.$ \begin{aligned} -5 + 6i – (-8) &= -5 + 6i + 8\\&= (-5 + 8) + 6i\\ &= 3 + 6i\end{aligned}$This means that when $-8$ is subtracted from $-5 + 6i$, the result is $3 + 6i$.

Example 2

What is the result when $12 – 8i$ is subtracted from $4i$? SolutionWe’re looking for the value of $4i – (12 – 8i)$. Distributing the negative sign properly is a crucial part of this problem.Combine the real and imaginary number parts, then simplify the result further, as shown below.$ \begin{aligned} 4i – (12 – 8i) &= 4 – 1(12) – (-8i)\\&= 4 + 12 + 8i\\&= (4 + 12) + 8i\\&=16 + 8i\end{aligned}$Hence, when $12 – 8i$ is subtracted from $4i$, the result is $16+ 8i$.

Example 3

What is the result when $15- 3i$ is subtracted from $6i + 12$? SolutionMake sure that we take note which of the two complex numbers are placed before and after the word “from,” so we’re actually looking for $(6i + 12) – (15 – 13i)$. Rearrange the terms in the first group so that the real number goes first.Distribute the negative sign after then combine like terms.$ \begin{aligned} (6i + 12) – (15 – 13i) &= (12 + 6i) – ( 15 – 13i)\\&= 12 + 6i – 15 – 13i\end{aligned}$We can then group the real and imaginary number parts then simplify the resulting difference.$ \begin{aligned} 12 + 6i – 15 – 13i &= (12 – 15) + (6 – 13)i\\&= 3 – 3i\end{aligned}$This shows that when $15- 3i$ is subtracted from $6i + 12$, the result is $3 – 3i$.

Example 4

Evaluate and simplify the following expressions.a. $(4 – 2i) – (3 + 5i) – (-6 – 9i)$ b. $[(12i – 8) – (10 – 4i)] – [(-6i – 15) – (8 + 10i)]$SolutionLet’s start with the first expression and simultaneously distribute the negative signs into the second and third sgroups of complex numbers.$\begin{aligned} (4 – 2i) – (3 + 5i) – (-6 – 9i) &= 4- 2i -(3) – (5i) -(-6) – (-9i)\\&= 4- 2i – 3 – 5i + 6 + 9i \end{aligned}$Now, let’s group all the real numbers and the imaginary numbers. Simplify each group to find the final value of the expression.$\begin{aligned}4- 2i – 3 – 5i + 6 + 9i &= (4 – 3 +6) + (-2i – 5i + 9i)\\&= (4 – 3 + 6) + (-2 – 5 + 9)i\\&= 7 + 2i \end{aligned}$a. This means that $(4 – 2i) – (3 + 5i) – (-6 – 9i)$ is equal to $7 + 2i$.We’re working with four complex numbers grouped into two subgroups. What we can do is find the difference between the two complex numbers in each bracket.Some reminders to remember:

Make sure that the complex number is of the form $a + bi$.
Distribute the negative signs carefully to avoid any mistake at the first stage.
Simplify by combining like the real and imaginary numbers.

$\boldsymbol{[(12i – 8) – (10 – 4i)]}$	$\boldsymbol{[(-6i – 15) – (8 + 10i)]}$
$\begin{aligned}(12i – 8) – (10 – 4i) &= (-8 + 12i) – (10 – 4i)\\&= -8 + 12i – 10 + 4i\\&= (-8 – 10) + (12 + 4)i\\&= -18 + 16i\end{aligned}$	$\begin{aligned}(-6i – 15) – (8 + 10i) &= (-15 – 6i) – (8 + 10i)\\&= -15 – 6i – 8 – 10i\\&= (-15 – 8) + (-6 -10)i\\&= -23 -16i \end{aligned}$

Let’s replace these differences into the corresponding brackets and evaluate the new expression once more.$\begin{aligned} (-18 + 16i) – (-23 – 16i) &= -18 + 16i + 23 + 16i\\&= (-18 + 23) + (16 + 16)i \\&= 5 + 32i \end{aligned}$Hence, we’ve shown that the original complex expression has now been simplified to $5 + 32i$.

Example 5

Evaluate and simplify $[(4 + \sqrt{-36}) – (-3 – \sqrt{-49})] – [(-6 – \sqrt{-16}) – (12 – \sqrt{-81})]$.SolutionWe can see four square roots that contain negative values inside, so let’s rewrite these terms first in terms of $i$.

$\sqrt{-36} = \sqrt{36} \cdot \sqrt{-1} = 6i$
$\sqrt{-49} = \sqrt{49} \cdot \sqrt{-1} = 7i$
$\sqrt{-16} = \sqrt{16} \cdot \sqrt{-1} = 4i$
$\sqrt{-81} = \sqrt{81} \cdot \sqrt{-1} = 9i$

Hence, we have $[(4 + 6i) – (-3 – 7i)] – [(-6 – 4i) – (12 – 9i)]$. Let’s go ahead and simplify the expressions inside each pair of brackets first.$\begin{aligned}[(4 + 6i) – (-3 – 7i)] – [(-6 – 4i) – (12 – 9i)]&= [4 + 6i -(-3) -(-7i)] – [-6 – 4i -(12) -(-9i)]\\&= (4 + 6i + 3 + 7i) – (-6 – 4i – 12 + 9i)\\&= (7 + 13i) – (-18 + 5i) \end{aligned}$Let’s simplify the expression further by finding the difference of the two remaining complex numbers.$\begin{aligned}(7 + 13i) – (-18 + 5i) &= (7 – -18) + (13 – 5)i\\&= 25 + 8i\end{aligned}$Hence, we have $[(4 + \sqrt{-36}) – (-3 – \sqrt{-49})] – [(-6 – \sqrt{-16}) – (12 – \sqrt{-81})] = 25+ 8i$.

Example 6

Show that the commutative property does not apply to the subtraction of complex numbers. SolutionLet $a + bi$ and $m + ni$ be the two complex numbers we want to subtract. To prove that subtraction of two complex numbers is not commutative, we want to show that $(a + bi) – (m + ni) \neq (m + ni) – (a + bi)$.We can evaluate the difference between the two expressions shown on the left and the right-hand side. We can apply the following steps to make sure we get the right expressions:

Distribute the negative signs correctly.
Group the real and imaginary number parts.
Simplify the expressions to find the difference of the two.

$\boldsymbol{(a + bi) – (m + ni)}$	$\boldsymbol{(m + ni) – (a + bi)}$
$\begin{aligned} (a + bi) – (m + ni) &= a + bi -m – ni\\&= (a – m) + (bi – ni)\\&= (a – m) + (b -n)i\end{aligned}$	$\begin{aligned} (m + ni) – (a + bi) &= m + ni – a- bi\\&= (m – a) + (ni – bi)\\&= (m – a) + (n -b)i\end{aligned}$

Since subtraction for real numbers is not commutative, $a – m \neq m – a$ and $b – n \neq n – b$.Hence, $(a – m) + (b -n)i \neq (m – a) + (n -b)i$ and consequently, this confirms that subtraction of complex numbers is not commutative as well.