Surface Area of a Cube – Explanation & Examples

Finding the surface area of an object is important if you want to determine how much material is needed to cover an object’s surface.

For example, companies that package items in carton boxes require the surface area to determine how much cardboard would be needed to make the box.

The surface area of a cube is the total sum of the area of all the six squares that cover a square.

In this article, we will learn how to find the surface area of a cube using the surface area of a cube formula.

How to Find the Surface Area of a Cube?

To recall, a cube is a 3-dimensional figure with 6 equal square faces, 8 edges, and 8 vertices. Since a cube has six faces, a cube’s surface area is found by multiplying the area of one square face by 6.

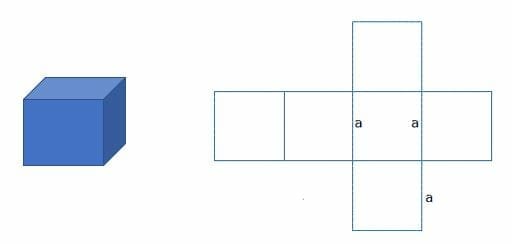
As for other areas, an object’s surface area is measured in square units, i.e., mm², cm², m².

Surface area of a cube formula

From the above illustration, the surface area of a cube is equal to:

Surface area of a cube = a² + a² + a² + a² + a² + a²

Therefore, the surface area of a cube formula is given as:

Surface area of a cube = 6a²

where a = any side length of a cube.

Let’s work out some example problems involving the surface area of a cube.

Example 1

Find the surface area of a cube of a side length of 10 cm.

Solution

By the formula,

Surface area of a cube = 6a²

= 6 x 10²

= 6 x 100

= 600 cm²

Example 2

Find the surface of a cube whose volume is 343 m³.

Solution

Given

Volume of a cube, a³ = 343 m³

First find the length of the cube

a = ³√343

a = 7 m

SA = 6a²

= 6 x 7²

= 6 x 49

= 294 m²

Example 3

The surface area of a cube is 150 feet square. What is the length of the cube?

Solution

Given, surface area = 150 ft²

SA = 6a²

150 = 6a²

Divide both sides by 6 to get,

25 = a²

√a = 5

Therefore, the length of the cube is 5 feet.

Example 4

A solid cube of length 10 m is to be painted on its 6 faces. If the painting rate is $ 10 per square meter, find the total cost of painting the cube.

Solution

To find the total cost of painting a cube, we multiply the cube’s surface area by the rate of painting.

SA = 6a²

= 6 x 10²

= 6 x 100

= 600 m²

The cost of painting = 600 m² x $ 10 per m²

= $6000.

Example 5

The height of a cubical tank is 12 feet. Find the surface area of the tank.

Solution

SA = 6a²

= 6 x 12²

= 6 x 144

= 864 ft²

Example 6

What is the length of the side of a cube whose surface area is equal to its volume?

Solution

Given:

Surface area of a cube = volume of a cube

6a² = a³

Divide both sides by a²

6a²/a² = a³/a²

6 = a

Therefore, the length of the cube is 6 units.

Example 7

Find the surface area of a cube whose diagonal is 12 yards.

Solution

For a cube, the length of the diagonal = √3a

where a = side length of a cube.

Therefore,

12 = √3a

Square both sides and then divide by 3.

144 = 3a

a = 48

Now, calculate the surface area of the cube

SA = 6a²

= 6 x 48 x 48

= 13824 square yards

Example 8

A rectangular cardboard is 0. 5 m long and 0.3 m wide. How many cubical boxes of length 5 cm can be made from cardboard?

Solution

The area of the rectangular cardboard = 0.5 x 0.3

= 0.15 m² ⇒ 1,500 cm²

Surface area of a cubical box = 6a²

= 6 x 5²

= 6 x 25

= 150 cm²

To get the number of boxes, divide the area of the card by the surface area of a cube

Number of boxes = 1,500/150

= 10 boxes.

Example 9

The cost of 1 m² of a card is $ 0.5. Find the cost of making 60 cubical boxes of length 0. 4 m.

Solution

First, determine the surface area of the 60 boxes

SA of a box = 6a²

= 6 x 0.4²

= 6 x 0.16

= 0.96 m²

Surface area of 60 boxes = 0.96 x 60

= 57.6 m²

The cost of making 60 boxes = 57.6 x 0.5

= $28.8

Example 10

The surface area of a cube is 1014 in². What is the volume of the cube?

Solution

SA = 6a²

1014 = 6a²

a² = 169

a = √169

a =13

The volume of a cube = a³

= 13 x 13 x 13

= 2197 in³.