JUMP TO TOPIC
Surface Area of a Cylinder – Explanation & Examples
Before we jump into the topic of a cylinder’s surface area, let’s review a cylinder. In geometry, a cylinder is a three-dimensional figure with two circular bases parallel to each other and a curved surface.
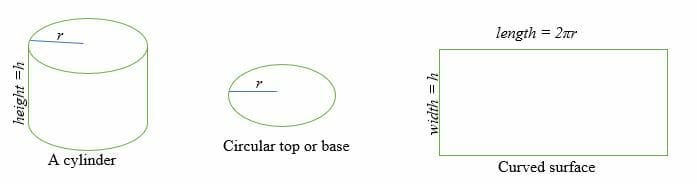
How to Find the Surface Area of a Cylinder?
The surface area of a cylinder is the sum of two parallel and congruent circular faces and the curved surface area.
This article will discuss how to find the total surface area and lateral surface area of a cylinder.
To calculate the surface area of a cylinder, you need to find the Base Area (B) and Curved Surface Area (CSA). Therefore, the surface area or the total surface of a cylinder is equal to the sum of the base area times two and the area of the curved surface.
The curved surface of a cylinder is equal to a rectangle whose length is 2πr and whose width is h.
Where r = radius of the circular face and h = height of the cylinder.
The area of the curved surface = Area of a rectangle =l x w = πdh
The base area, B = Area of a circle = πr2
The area of a cylinder formula
The formula for the total surface area of a cylinder is given as:
Total surface area of a cylinder = 2πr2 + 2πrh
TSA = 2πr2 + 2πrh
Where 2πr2 is the top and bottom circular face area, and 2πrh is the area of the curved surface.
By taking 2πr as a common factor from RHS, we get;
TSA = 2πr (h + r) ……………………………………. (Surface area of a cylinder formula)
Let’s solve example problems involving the surface area of a cylinder.
Example 1
Find the total surface area of a cylinder whose radius is 5 cm and height is 7 cm.
Solution
By the formula,
TSA = 2πr (h + r)
= 2 x 3.14 x 5(7 + 5)
= 31.4 x 12
= 376.8 cm2
Example 2
Find the radius of a cylinder whose total surface area is 2136.56 square feet, and the height is 3 feet.
Solution
Given:
TSA = 2136.56 square feet
Height, h = 3 feet
But, TSA = 2πr (h + r)
2136.56 =2 x 3.14 x r (3 + r)
2136.56 = 6.28r (3 + r)
By distributive property of multiplication on the RHS, we have,
2136.56 = 18.84r + 6.28r2
Divide each term by 6.28
340.22 = 3r + r2
r2 + 3r – 340.22 = 0 ……… (a quadratic equation)
By solving the equation using the quadratic formula, we get,
r = 17
Therefore, the radius of the cylinder is 17 feet.
Example 3
The cost of painting a cylindrical container is $0.04 per cm2. Find the cost of painting 20 containers of radius, 50 cm, and height, 80 cm.
Solution
Calculate the total surface area of 20 containers.
TSA = 2πr (h + r)
= 2 x 3.14 x 50 (80 + 50)
= 314 x 130
= 40820 cm2
The total surface area of 20 containers = 40,820 cm2 x 20
=816,400 cm2
The cost of painting = 816,400 cm2 x $0.04 per cm2
= $32,656.
Hence, the cost of painting 20 containers is $32,656.
Example 4
Find the height of a cylinder if its total surface area is 2552 in2 and the radius is 14 in.
Solution
Given:
TSA = 2552 in2
Radius, r = 14 in.
But, TSA = 2πr (h + r)
2552 = 2 x 3.14 x 14 (14 + h)
2552 = 87.92(14 + h)
Divide both sides by 87.92 to get,
29.026 = 14 + h
Subtract by 14 on both sides.
h = 15
Hence, the height of the cylinder is 15 in.
Lateral Surface Area of a Cylinder
As stated before, the area of the curved surface of a cylinder is what is termed as the lateral surface area. In simple words, a cylinder’s lateral surface area is the surface area of a cylinder, excluding the area of the base and bottom (circular surface).
The formula gives the lateral surface area of a cylinder;
LSA = 2πrh
Example 5
Find the later surface area of a cylinder whose diameter is 56 cm and height is 20 cm.
Solution
Given:
Diameter = 56 cm, hence radius, r =56/2 = 28 cm
Height, h = 20 cm
By, the formula,
LSA = 2πrh
= 2 x 3.14 x 28 x 20
= 3516.8 cm2.
Thus, the lateral surface area of the cylinder is 3516.8 cm2.
Example 6
The lateral surface area of a cylinder is 144 ft2. If the radius of the cylinder is 7 ft, find the height of the cylinder.
Solution
Given;
LSA = 144 ft2
Radius, r = 7 ft
144 = 2 x 3.14 x 7 x h
144 = 43.96h
Divide by 43.96 on both sides.
3.28 = h
So, the height of the cylinder is 3.28 ft.
