JUMP TO TOPIC
This question aims to find the area bounded by two circles using the double integral.
A bounded region is defined by a boundary or by a set of constraints. More specifically, a bounded region cannot be regarded as an infinitely large area it is usually determined by a set of parameters or measurements.
The area of a region, the volume under the surface, and the average value of the function of two variables over a rectangular region are determined by double integral. The surface integral can be referred to as a generalization of the double integral. There are two types of regions for which the area can be calculated. The first one is the Type I region which is bounded by the lines $x=a$ and $x=b$ as well as the curves $y=g(x)$ and $y=h(x)$ with the assumption that $g(x)<h(x)$ and $a<b$. In this case, the integration can be performed as: $\int\int_{R}f(x,y)dA=\int\limits_{x=a}^{b}\int\limits_{y=g(x)}^{h(x)}f(x,y)dydx$.
The second one is the Type II region which is bounded by the lines $y=c$ and $y=d$ as well as the curves $x=g(y)$ and $x=h(y)$ with the assumption that $g(y)<h(y)$ and $c<d$. In this case, the integration can be performed as: $\int\int_{R}f(x,y)dA=\int\limits_{y=c}^{d}\int\limits_{x=g(y)}^{h(y)}f(x,y)dxdy$.
Expert Answer
To better understand the problem, the two circles are drawn and the required area is shaded in the following figure.
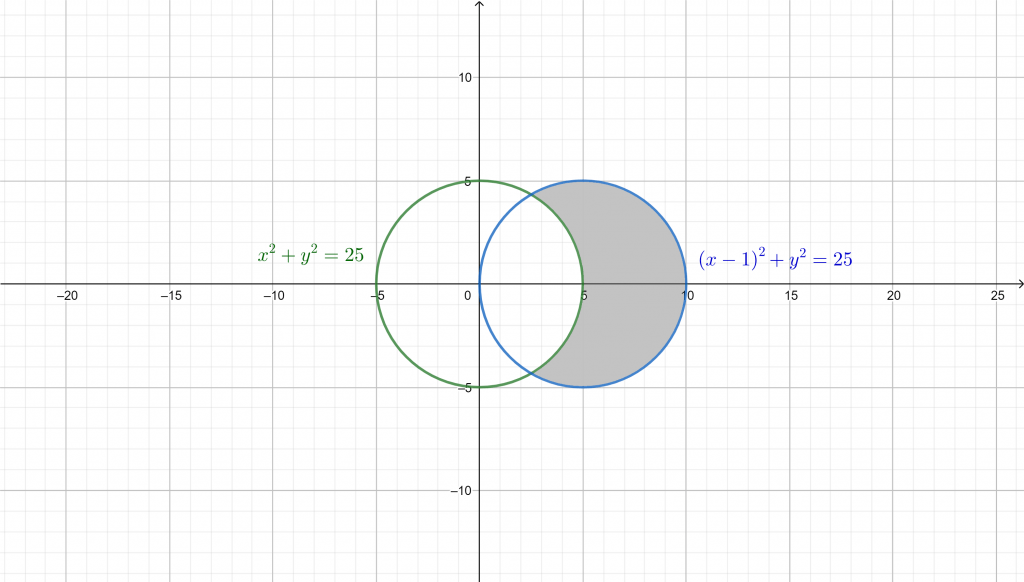
First, convert both the equations to the polar form. Since:
$x=r\cos\theta$ and $y=r\sin\theta$, therefore, for $(x-5)^2+y^2=25$ we have:
$(r\cos\theta-5)^2+(r\sin\theta)^2=25$
$r^2\cos^2\theta-10r\cos\theta+25+r^2\sin^2\theta=25$
$r^2-10r\cos\theta=0$
$r^2=10r\cos\theta$
$r=10\cos\theta$ (1)
And for $x^2+y^2=25$, we have:
$r^2\cos^2\theta+r^2\sin^2\theta=25$
$r^2=25$
$r=5$ (2)
Now, equate (1) and (2) to find the limits of integration:
$5=10\cos\theta$
$1=2\cos\theta$
$\cos\theta=\dfrac{1}{2}$
Or $\theta=\pm\, \dfrac{\pi}{3}$
Now, set up the integral to find the area of the region as:
$\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\int\limits_{5}^{10\cos\theta}rdrd\theta$
First, performing integration with respect to $r$:
$=\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left|\dfrac{r^2}{2}\right|_{5}^{10\cos\theta}\,d\theta$
$=\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left[\dfrac{(10\cos\theta)^2}{2}-\dfrac{(5)^2}{2}\right]\,d\theta$
$=\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left[\dfrac{100\cos^2\theta}{2}-\dfrac{25}{2}\right]\,d\theta$
$=\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left[50\cos^2\theta-\dfrac{25}{2}\right]\,d\theta$
Now since $\cos^2\theta=\dfrac{\cos2\theta+1}{2}$, therefore:
$=\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left[50\left(\dfrac{\cos2\theta+1}{2}\right)-\dfrac{25}{2}\right]\,d\theta$
$=\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left[25\cos2\theta+25-\dfrac{25}{2}\right]\,d\theta$
$=\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left[25\cos2\theta+\dfrac{25}{2}\right]\,d\theta$
$=25\int\limits_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\left[\cos2\theta+\dfrac{1}{2}\right]\,d\theta$
$=25\left[\dfrac{\sin2\theta}{2}+\dfrac{\theta}{2}\right]_{-\frac{\pi}{3}}^{\frac{\pi}{3}}$
$=\dfrac{25}{2}\left[\sin\left(\dfrac{2\pi}{3}\right)+\left(\dfrac{\pi}{3}\right)-\sin\left(-\dfrac{2\pi}{3}\right)-\left(-\dfrac{\pi}{3}\right)\right]$
$=\dfrac{25}{2}\left[\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{3}\right]$
$=\dfrac{25}{2}\left[\sqrt{3}+\dfrac{2\pi}{3}\right]$
$=\dfrac{25\sqrt{3}}{2}+\dfrac{25\pi}{3}$
Hence, area of the region inside the circle $(x-5)^2+y^2=25$ and outside the circle $x^2+y^2=25$ is $\dfrac{25\sqrt{3}}{2}+\dfrac{25\pi}{3}$.
Example 1
Evaluate the double integral $\int\limits_{-1}^{1}\int\limits_{2}^{3}\dfrac{x}{y^3}\, dx dy$.
Solution
Rewrite the integral as:
$\int\limits_{-1}^{1}\int\limits_{2}^{3}\left(\dfrac{x}{y^3}\, dx\right) dy$
Or, $\int\limits_{-1}^{1}\dfrac{1}{y^3}\left(\int\limits_{2}^{3}x\, dx\right) dy$
$=\int\limits_{-1}^{1}\dfrac{1}{y^3}\left(\left[\dfrac{x^2}{2}\right]_{2}^{3}\right) dy$
$=\int\limits_{-1}^{1}\dfrac{1}{y^3}\left[\dfrac{(3)^2}{2}-\dfrac{(2)^2}{2}\right]dy$
$=\int\limits_{-1}^{1}\dfrac{1}{y^3}\left[\dfrac{9}{2}-2\right]dy$
$=\int\limits_{-1}^{1}\dfrac{1}{y^3}\left[\dfrac{5}{2}\right]dy$
$=\dfrac{5}{2}\int\limits_{-1}^{1}\dfrac{1}{y^3}dy$
$=\dfrac{5}{2}\left[-\dfrac{1}{2y^2}\right]_{-1}^{1}$
$=\dfrac{5}{2}\left[-\dfrac{1}{2(1)^2}+\dfrac{1}{2(-1)^2}\right]$
$=\dfrac{5}{2}\left[-\dfrac{1}{2}+\dfrac{1}{2}\right]$
$=\dfrac{5}{2}(0)$
$=0$
Example 2
Evaluate the double integral $\int\limits_{0}^{1}\int\limits_{3}^{4}x^2y\, dx dy$.
Solution
Rewrite the integral as:
$\int\limits_{0}^{1}\int\limits_{3}^{4}\left(x^2y\, dx\right) dy$
Or, $\int\limits_{0}^{1}y\left(\int\limits_{3}^{4}x^2\, dx\right) dy$
$=\int\limits_{0}^{1}y\left(\left[\dfrac{x^3}{3}\right]_{3}^{4}\right) dy$
$=\int\limits_{0}^{1}y\left[\dfrac{(4)^3}{3}-\dfrac{(3)^3}{3}\right]dy$
$=\int\limits_{0}^{1}y\left[\dfrac{64}{3}-9\right]dy$
$=\int\limits_{0}^{1}y\left[\dfrac{37}{3}\right]dy$
$=\dfrac{37}{3}\int\limits_{0}^{1}y\,dy$
$=\dfrac{37}{3}\left[\dfrac{y^2}{2}\right]_{0}^{1}$
$=\dfrac{37}{3}\left[\dfrac{(1)^2}{2}-\dfrac{(0)^2}{2}\right]$
$=\dfrac{37}{3}\left[\dfrac{1}{2}-0\right]$
$=\dfrac{37}{3}\left[\dfrac{1}{2}\right]$
$=\dfrac{37}{6}$
Images/mathematical drawings are created with GeoGebra.
