
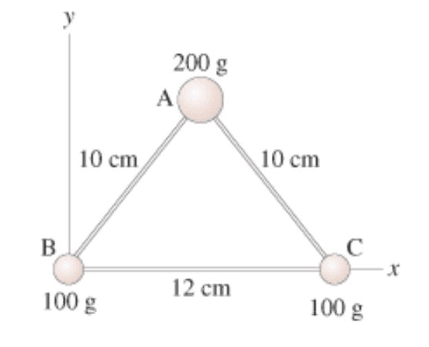
This question aims to find the moment of inertia about the given axis of rotation.
Inertia is a property of a body that opposes any force which attempts to move it or to change the magnitude or direction of its velocity if it is in motion. Inertia is a non-resistant property that allows a body to oppose active factors such as forces and torques.
The moment of inertia is defined as a quantitative measure of a body’s rotational inertia, that is, the body’s resistance to having its rotation speed about an axis changed by the implementation of torque or a turning force. It is determined by the mass distribution of the body and the axis to be chosen, with larger moments necessitating more torque to alter the rate of rotation of a body. The axis may or may not be fixed and can be internal or external.
The moment of inertia of a point mass is simply the mass multiplied by the square of the perpendicular distance to the rotation axis, $I = mr^2$. Because any object can be constructed from a collection of point masses, the point mass relationship becomes the foundation for all other moments of inertia. During linear motion, the moment of inertia plays the same role as the mass, which is the measurement of a body’s resistance to a change in rotational motion. It is constant for a specific rigid frame and axis of rotation.
Expert Answer
The distance of the masses $B$ and $C$ is $10\, cm$ from the mass $A$.
Let $m_1$ be the mass of $B$, then $m_1=100\,kg$
and let $m_2$ be the mass of $C$, then $m_2=100\,kg$
The moment of inertia about an axis passing through $A$ and perpendicular to the page is:
$I=m_1r^2_1+m_2r^2_2$
$I=(100)(10)^2+(100)(10)^2$
$I=2.0\times 10^4\,g\,cm^2$
Let $a$ be the distance of $A$ from the $x-$axis then:
$a^2+6^2=10^2$
$a^2+36=100$
$a^2=100-36$
$a^2=64$
$a=8\,cm$
Masses $B$ and $C$ will not have any effect on the moment of inertia because they lie on the axis. So, the moment of inertia of the system about the axis passing through masses $B$ and $C$ is:
$I=mr^2$
Here, $m=200\,g$ and $r=8\,cm$
So, $I=(200)(8)^2$
$I=1.28\times 10^4\,g\,cm^2$
Example
A $50\, g$ mass is linked to one end of a cord having the length $10\, cm$. Find the moment of inertia of the mass if the axis of rotation is $AB$.
Solution
Here, $AB$ is the axis of rotation.
Mass $(m)=50\,g=0.05\,kg$
$r=10\,cm=0.1\,m$
Therefore, moment of inertia will be:
$I=mr^2$
$I=(0.05\,kg)(0.1\,m)^2$
$I=(0.05\,kg)(0.01\,m^2)$
$I=0.0005\,kg\,m^2$
