Find the Taylor polynomial T3(x) for the function f centered at the number a. f(x) = x + e^{−x}, a = 0

This problem aims to find the Taylor polynomials up to $3$ places for a given function $f$, centered at a point $a$. To better understand the problem, you must know about Power Series, as it forms the basis of the Taylor Series.

Taylor series of a function is defined as an infinite sum of derivative terms of that function at a single point. The formula for this Series is derived from the Power series and can be written as:

\[ \sum_{k=0}^{\infty} \dfrac{f^{k}(a)}{k!} (x-a)^k \]

where $f^(k)(a)$ denotes the nth derivative of $f$ evaluated at point $a$ and $k$ is the degree of the polynomial. If $a$ is set to 0, it’s known as Maclaurin Series.

But not every function has a Taylor Series expansion.

Expert Answer:

Firstly, expanding the series for $k = 3$ as $T3$

\[  T3(x) = f(a) + \dfrac{f`(a)}{1!}(x-a) + \dfrac{f“(a)}{2!}(x-a)^ 2 + \dfrac{f“`(a)}{3!}(x-a)^ 3 \]

Next, we are going to find the derivatives of $f(x)$ which will get plugged into $T3(x)$ equation:

\[ f(x) =x + e^{-x},      f(0) = 1 \]

First Derivative:

\[ f`(x) = 1 – e^{-x},     f`(0) = 0 \]

Second Derivative:

\[ f“(x) = e^{-x},         f“(0) = 1 \]

Third Derivative:

\[ f“`(x) = – e^{-x},     f“`(0) = -1 \]

Substituting the above derivatives into $T3(x)$ becomes:

\[ T3(x) = f(a) +\dfrac{f`(a)}{1!}(x-a) + \dfrac{f“(a)}{2!}(x-a)^2 + \dfrac{f“`(a)}{3!}(x-a)^ 3 \]

Simplifying the equation:

\[ = 1 +\dfrac{0}{1!}(x-0) + \dfrac{1}{2!}(x-2)^ 2 + \dfrac{-1}{3!}(x-0)^ 3 \]

\[ T3(x) = 1 +\dfrac{x^ 2} {2} – \dfrac{x^ 3} {6} \]

Numerical Result:

Finally, we have our Taylor Series Expansion:

\[ T3(x) = 1 +\dfrac{x^ 2} {2} – \dfrac{x^ 3} {6} \]

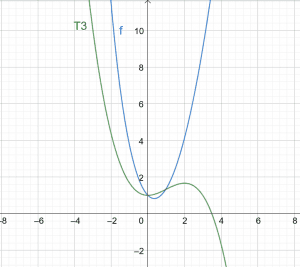
Figure 1

Example:

Find the taylor polynomial $t3(x)$ for the function $f$ centered at the number a. $f(x) = xcos(x), a = 0$

Expanding the series for $k = 3$ as $T3$ gives us:

\[  T3(x) = f(a) + \dfrac{f`(a)}{1!}(x-a) + \dfrac{f“(a)}{2!}(x-a)^ 2 + \dfrac{f“`(a)}{3!}(x-a)^ 3 \]

Next, we are going to find the derivatives of $f(x)$ which will get plugged into $T3(x)$ equation:

\[ f(x) =xcos(x),                         f(0) = 0 \]

\[ f`(x) = cos(x) – xsin(x),         f`(0) = 1 \]

\[ f“(x) = -xcos(x) -2sin(x),     f“(0) = 0 \]

\[ f“`(x) = xsin(x) -3cos(x),     f“`(0) = -1 \]

Substituting the above derivatives into $T3(x)$ becomes:

\[ T3(x) = f(a) +\dfrac{f`(a)}{1!}(x-a) + \dfrac{f“(a)}{2!}(x-a)^ 2 + \dfrac{f“`(a)}{3!}(x-a)^ 3 \]

Plugging in the values in $T3(x)$ equation.

\[ = \dfrac{1}{1!}x + 0 + \dfrac{-3}{3!}x^ 3  \]

Finally, we have our Taylor Series Expansion:

\[ T3(x) = x – \dfrac{1}{2}x^ 3  \]

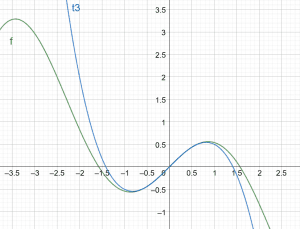
Figure 2