- Home
- >
- Trigonometric derivatives – Derivation, Explanation, and Examples
JUMP TO TOPIC
Trigonometric derivatives – Derivation, Explanation, and Examples
 Trigonometric derivatives will show us how even periodic functions like $y = \sin x$ and $y = \cos x$ will exhibit periodic functions as well. Having a list of derivative rules for common trigonometric expressions comes in handy when you’re working with oscillating functions. Learning how to differentiate different trigonometric functions will help observe objects in harmonic motions’ velocity and acceleration – which is extremely helpful in physics, engineering, and even finance.
Trigonometric derivatives will show us how even periodic functions like $y = \sin x$ and $y = \cos x$ will exhibit periodic functions as well. Having a list of derivative rules for common trigonometric expressions comes in handy when you’re working with oscillating functions. Learning how to differentiate different trigonometric functions will help observe objects in harmonic motions’ velocity and acceleration – which is extremely helpful in physics, engineering, and even finance.
Trigonometric derivatives are also periodic in nature. Deriving these rules will help us understand how to differentiate simple and complex functions that contain trigonometric expressions.
In this article, we’ll learn the six fundamental trigonometric derivatives, learn when to apply them, and understand how some of these derivative rules were derived (we might even leave some for you in the exercise section to work on!).
Here are some concepts that you’d want to brush up on to make the most out of our discussions:
- Recall the six trigonometric functions, how they related to each other, and helpful trigonometric identities.
- We’ll also need the limits of some trigonometric expressions.
- Make sure to have your handy list of derivative rules with you as well.
For now, let’s go ahead and understand how some of these rules were derived and how we can apply them to differentiate complex trigonometric functions.
What is a trigonometric derivatives?
The trigonometric derivatives will represent the trigonometric functions’ rates of change at a given variable, $x$.
We’ve learned about the six trigonometric functions as shown in trigonometry and precalculus classes.
\begin{aligned}\sin x &= \dfrac{1}{\csc x},\phantom{xxx} \csc{x} = \dfrac{1}{\sin x}\\\cos x &= \dfrac{1}{\sec x},\phantom{xxx} \sec{x} = \dfrac{1}{\cos x}\\\tan x &= \dfrac{1}{\cot x},\phantom{xxx} \cot{x} = \dfrac{1}{\tan x}\end{aligned}
As expected, these six functions are expected to have their corresponding derivatives. Hence, our need for the six trigonometric derivatives.
For example, the graph below shows how the derivative of $f(x)= \sin x$, will behave throughout the interval, $[-2\pi, 2\pi]$.
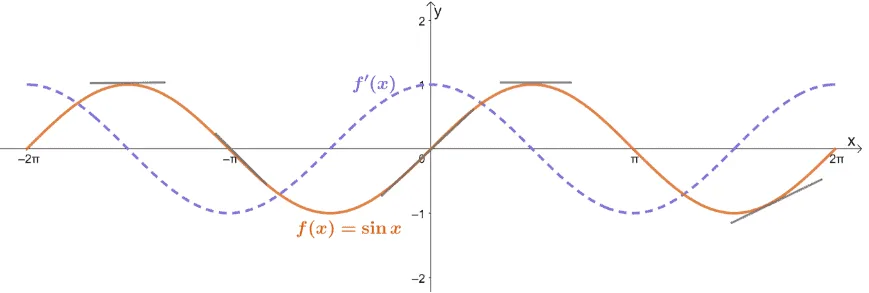
Does the graph of $f'(x)$ look familiar? Yes, it’s the graph of $y = \cos x$ and that’s because $\dfrac{d}{dx} \sin x = \cos x$. Here’s a table that lists down the six trigonometric derivatives:
| Six Trigonometric Derivatives | |
| \begin{aligned}\dfrac{d}{dx} \sin x &= \cos x\\\text{Domain} &: -\infty<x<\infty \end{aligned} | \begin{aligned}\dfrac{d}{dx} \csc x &= -\cot x\csc x\\\text{Domain } x&\neq \pi n, n\in Z \end{aligned} |
| \begin{aligned}\dfrac{d}{dx} \cos x &= -\sin x\\\text{Domain} &: -\infty<x<\infty \end{aligned} | \begin{aligned}\dfrac{d}{dx} \sec x &= \tan x \sec x\\\text{Domain } x&\neq \dfrac{\pi}{2}+ \pi n, n\in Z \end{aligned} |
| \begin{aligned}\dfrac{d}{dx} \tan x &= \sec^2 x\\\text{Domain } x&\neq \dfrac{\pi}{2}+ \pi n, n\in Z \end{aligned} | \begin{aligned}\dfrac{d}{dx} \cot x &= -\csc^2 x\\\text{Domain } x&\neq \pi n, n\in Z \end{aligned} |
These are the six fundamental trigonometric derivatives that we’ll need for us to differentiate different trigonometric functions. Of course, the rest of the derivative rules we’ve learned in the past will be important as well when differentiating complex functions with trigonometric expressions.
To better understand and appreciate these six rules, we’ll show you how to differentiate $\dfrac{d}{dx} \sin x$. This can act as a guide for you also to try deriving some of these trigonometric derivatives.
How to derive the rules for $\boldsymbol{\dfrac{d}{dx} \sin x}$ and $\boldsymbol{\dfrac{d}{dx} \cos x}$?
In the past, we’ve learned that $\lim_{h\rightarrow 0}\dfrac{\sin h}{h} = 1$ and $\lim_{h\rightarrow 0}\dfrac{\cos h – 1}{h} = 0$. These two trigonometric limits will come in handy when we want to prove the fact that $\dfrac{d}{dx} \sin x = \cos x$.
Using the definition of $f(x)$’s derivative, we have the following for $\dfrac{d}{dx} \sin x$.
\begin{aligned}\dfrac{d}{dx} \sin x &= \lim_{h \rightarrow 0} \dfrac{\sin (x +h) – \sin x}{h}\end{aligned}
We can expand $\sin(x + h)$ using the sum formula for sine; we can rewrite the expression for the derivative of $\sin x$.
\begin{aligned}\dfrac{d}{dx} \sin x &= \lim_{h \rightarrow 0} \dfrac{(\sin x \cos h + \cos x \sin h) – \sin x}{h}\\&= \lim_{h \rightarrow 0} \dfrac{(\sin x \cos h -\sin x ) + \cos x \sin h}{h}\\&= \lim_{h \rightarrow 0} \dfrac{\sin x(\cos h -1 ) + \cos x \sin h}{h}\end{aligned}
Keep in mind for that for this case, $\sin x$ and $\cos x$ are constants in this expression. We can then rewrite this so that we can substitute $\lim_{h\rightarrow 0}\dfrac{\sin h}{h} $ and $\lim_{h\rightarrow 0}\dfrac{\cos h – 1}{h}$ with $1$ and $0$, respectively.
\begin{aligned}\dfrac{d}{dx} \sin x &= \sin x\lim_{h \rightarrow 0} \dfrac{\cos h -1 }{h} + \cos x \lim_{h \rightarrow 0} \dfrac{\sin h}{h}\\&= (\sin x)(0) + (\cos x)(1)\\&= \cos x \end{aligned}
This confirms the fact that $\dfrac{d}{dx} \sin x = \cos x$. The process for deriving the derivative rule for cosine is similar, so you can try working on its full derivation on your own. Check the shortened proof below to confirm your work.
\begin{aligned}\dfrac{d}{dx} \cos x &= \lim_{h\rightarrow 0} \dfrac{\cos(x + h) – \cos x}{h}\\&= \lim_{h\rightarrow 0} \dfrac{(\cos x\cos h – \sin h\sin x) – \cos x}{h}\\&= \lim_{h\rightarrow 0} \dfrac{(\cos x\cos h – \cos x) – \sin h\sin x}{h}\\&= \cos x\lim_{h\rightarrow 0} \dfrac{\cos h – 1}{h} – \sin x\lim_{h\rightarrow 0} \dfrac{\sin h}{h}\\&= (\cos x)(0)- \sin x(1)\\&= -\sin x\end{aligned}
After using a similar process, we have shown that $\dfrac{d}{dx} \cos x$ is indeed equal to $-\sin x$. In fact, graphing these two functions will also confirm this rule.
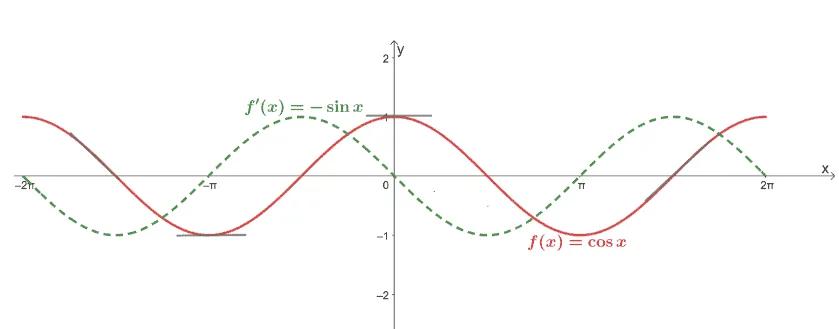
Now that we’ve explored the process of proving two of the most important trigonometric derivatives let’s take a look at different circumstances where we might have to apply these rules.
When to use a trigonometric derivatives?
Now that we know the six important trigonometric derivatives, it’s important to keep an eye on the following instances we might need to use these derivative rules:
- Whenever we’re asked to differentiate trigonometric functions, we’ll always go back to these six rules depending on our given function.
- Most of the time, we’ll also be using fundamental derivative rules along with the six given trigonometric derivatives.
- Most of the time, when the expression inside the trigonometric function contains terms with coefficients, the chain rule will still apply.
- We can also use these six trigonometric derivatives to prove the derivative of functions. For example, the expression for $\dfrac{d}{dx} \tan x$ can be derived using the derivative rules for sine and cosine as well as the quotient rule.
For now, we’ll show you how to derive $f(x) = 3\sin 3x – 2\cos x$ to show you how we might need some trigonometric derivatives and the other derivative rules we learned in the past.
- Since $f(x)$ is the difference between two terms, we can use the difference rule. Meaning, we can take the difference of the respective terms’ derivatives.
- We can then use the constant multiple rule to factor out $3$ and $2$ from each of the terms.
\begin{aligned}f'(x) &= {\color{green}\dfrac{d}{dx}3\sin 3x – \dfrac{d}{dx} 2\cos x},\phantom{x} \color{green}\text{Difference Rule}\\&= {\color{green}3}\dfrac{d}{dx}\sin 3x – {\color{green}2}\dfrac{d}{dx} \cos x,\phantom{x} \color{green}\text{Constant Multiple Rule}\end{aligned}
We can now simplify the second term since we know that $\dfrac{d}{dx} \cos x = -\sin x$. As for $\dfrac{d}{dx} \sin 3x$, make sure to apply the chain rule and remember to take the derivative of $3x$ as well.
\begin{aligned}f'(x) &= 3\dfrac{d}{dx}\sin 3x – 2{\color{green}(-\sin x)},\phantom{x} \color{green}\text{Derivative of Cosine}\\&= 3{\color{green}\cos 3x \cdot \dfrac{d}{dx} 3x} – 2(-\sin x),\phantom{x} \color{green}\text{Derivative of Sine & Chain Rule}\\&= (3\cos 3x){\color{green}(3x)} + 2\sin x,\phantom{x} \color{green}\text{Constant Multiple & Power Rules}\\&= 9x\cos 3x + 2\sin x\end{aligned}
Hence, we have $f'(x) = 9x \cos 3x + 2 \sin x$. This example shows how it’s important for us to master trigonometric derivatives. At the same time, it’s essential that at this point, we are now comfortable with the basic derivative rules. Head over to this link if you need a refresher and try out these examples we’ve prepared for you if you’re ready.
Example 1
Find the derivative of $f(x) = 3\sin x \cos x$.
Solution
Before differentiating any function, it helps to inspect it first. This will help you decide your own approach and know the rules that you might need to differentiate the given function.
- We can see that $f(x)$ has a coefficient of $3$ before $\sin x \cos x$, so we can use the constant multiple rule ($\dfrac{d}{dx} c\cdot f(x) = c \cdot \dfrac{d}{dx} f(x)$).
- We can then use the product rule to differentiate $\sin x \cos x$ properly.
\begin{aligned}f'(x) &= \dfrac{d}{dx} (3\sin x \cos x)\\&={\color{green}3}\dfrac{d}{dx} (\sin x \cos x) ,\phantom{x} \color{green}\text{Constant Multiple Rule}\\&=3{\color{green} \left[ \left( \dfrac{d}{dx} \sin x\right ) (\cos x) + \left(\dfrac{d}{dx} \cos x\right ) \sin x \right]} ,\phantom{x} \color{green}\text{Product Rule}\end{aligned}
We can then use the trigonometric derivatives, $\dfrac{d}{dx} \sin x = \cos x$ and $\dfrac{d}{dx} \cos x = -\sin x$ to further simplify the expression for $f'(x)$.
\begin{aligned}f'(x) &= 3\left[ {\color{green}(\cos x)} (\cos x) + \left(\dfrac{d}{dx} \cos x\right)( \sin x) \right] ,\phantom{x} \color{green}\text{Derivative for Sine}\\&= 3\left[ (\sin x) (\cos x) + {\color{green}(-\sin x)}( \sin x) \right] ,\phantom{x} \color{green}\text{Derivative for Cosine}\\&= 3(\cos^2 x – \sin^2 x)\end{aligned}
This shows that through different derivative rules, we have $f'(x) = 3(\cos^2 x – \sin^2 x)$. You can also use trigonometric identities (double-angle formula, as a matter of fact) to rewrite the expression, $f'(x) = 3 \cos 2x$.
Example 2
Find the derivative of $g(x) = \dfrac{\cos x}{2- \csc x}$.
Solution
We can see that $g(x)$ is a rational expression – with $\cos x$ as the numerator and $(2 – \csc x)$ as the denominator. This means that we’ll have to use the quotient rule first.
\begin{aligned}g'(x) &= \dfrac{d}{dx} \left(\dfrac{\cos x}{2- \csc x} \right )\\&={\color{green} \dfrac{(2 -\csc x) \dfrac{d}{dx} (\cos x) – \cos x \dfrac{d}{dx} (2- \csc x)}{(2 – \csc x)^2}}, \phantom{x}\color{green}\text{Quotient Rule}\end{aligned}
We can then use trigonometric derivatives for sine and cosecant, $\dfrac{d}{dx} \sin x = \cos x$ and $\dfrac{d}{dx} \csc x = -\cot x\csc x$, to rewrite the numerator.
\begin{aligned}g'(x) &= \dfrac{(2 -\csc x) {\color{green} (-\sin x)} – \cos x \dfrac{d}{dx} (2- \csc x)}{(2 – \csc x)^2}, \phantom{x}\color{green}\text{Derivative for Cosine}\\&= \dfrac{(2 -\csc x) (-\sin x) – \cos x {\color{green} \left(\dfrac{d}{dx} 2- \dfrac{d}{dx}\csc x\right)}}{(2 – \csc x)^2}, \phantom{x}\color{green}\text{Sum Rule}\\&= \dfrac{(2 -\csc x)(-\sin x) – \cos x {\color{green} \left(0+\cot x\csc x\right)}}{(2 – \csc x)^2}, \phantom{x}\color{green}\text{Constant Rule & Derivative for Cosecant}\end{aligned}
We can then simplify the expression further using trigonometric identities and have the following expression for $g'(x)$.
\begin{aligned}g'(x) &= \dfrac{-2\sin x +1 – (\cos x \cot x\csc x)}{(2 – \csc x)^2}\\&= \dfrac{-2\sin x +1 – \cos x \cdot \dfrac{\cos x}{\sin x}\cdot \dfrac{1}{\sin x} }{(2 – \csc x)^2}\\&= \dfrac{-2\sin x + 1 – \dfrac{\cos^2 x}{\sin^2 x}}{(2-\csc x)^2}\end{aligned}
Hence, we have $g'(x) = \dfrac{-2\sin x + 1 – \dfrac{\cos^2 x}{\sin^2 x}}{(2-\csc x)^2}$ or $g'(x) = \dfrac{-2\sin x + 1 – \cot^2 x}{(2-\csc x)^2}$.
Practice Questions
1. Find the derivative of each of the following functions.
a. $f(x) = 4 \cos x – 2\sin x$
b. $g(x) = -2 \sec x \cot 2x$
c. $h(x) = \dfrac{\cos x}{1 – 3\sin x}$
2.Use the first three trigonometric derivatives to prove that $\dfrac{d}{dx} \sec x = \tan x \sec x$ for all $x \neq \dfrac{\pi}{2}+ \pi n, n\in Z$.
3. Find the derivative of each of the following functions.
a. $f(x) = 4\sec x + 5 \cot x$
b. $g(x) = 2\sin x \cos x – 4\tan x$
c. $h(x) = 4x^2 – x^3 \tan 3x$
Answer Key
1.
a. $f'(x) = -4\sin x -2 \cos x$
b. $g'(x) = (2\sec x) (2 \csc^2 2x – \tan x \cot 2x)$
c.$h'(x) = \dfrac{(\sin x)(3 \sin x – 1) + 3\cos^2 x}{(1 – 3\sin x)^2}$
2.
$\begin{aligned}\dfrac{d}{dx} \sec x &= \dfrac{d}{dx} \dfrac{1}{\cos x}\\&= {\color{green}\dfrac{\cos x\dfrac{d}{dx} 1 – 1\dfrac{d}{dx} \cos x}{\cos^2{x}}},\phantom{x} \color{green}\text{Quotient Rule}\\&= \dfrac{(\cos x){\color{green} (0)} – 1 \dfrac{d}{dx} \cos x}{\cos^2 x},\phantom{x} \color{green}\text{Constant Rule}\\&= \dfrac{0 – 1 {\color{green}(-\sin x)}}{\cos^2 x},\phantom{x} \color{green}\text{Derivative of Sine}\\&= \dfrac{\sin x}{\cos^2 x}\\&= \dfrac{1}{\cos x}\cdot\dfrac{\sec x}{\cos x}\\&= \sec x \tan x\end{aligned}$
3.
a. $f'(x) = 4\tan x \sec x -5\csc^2 x$
b. $g'(x) = 2\cos^2 x- 2(\sin^2 x+ 2\sec^2 x)$
c.$h'(x) = -3x^3\sec^2 3x -3x^2 \tan 3x + 8x$
Images/mathematical drawings are created with GeoGebra.
