- Home
- >
- Trigonometric form – Definition, Example, and Explanation
JUMP TO TOPIC
Trigonometric Form – Definition, Example, and Explanation
 We can write complex numbers in terms of $r$ and $\theta$. This form is called the trigonometric form and is an essential form of complex numbers because it is much easier to find the roots and powers of complex numbers when they are in their trigonometric forms.
We can write complex numbers in terms of $r$ and $\theta$. This form is called the trigonometric form and is an essential form of complex numbers because it is much easier to find the roots and powers of complex numbers when they are in their trigonometric forms.
The trigonometric form of complex numbers contains the distance of the complex number’s coordinate from the origin and the angle formed by the real axis, and the segment connecting the complex number and the origin.
We often use the trigonometric form of complex numbers to illustrate them as quantities with distance and direction. When we want to find the powers and roots of complex numbers, it is also easier to find them when the complex numbers are in trigonometric form.
In this article, we’ll learn the following:
- The two important components of complex numbers in trigonometric or polar form.
- Converting complex numbers in standard form to trigonometric form.
- Finding the quotient and product of two complex numbers in trigonometric forms.
Let’s go ahead and dive right into the definition of complex numbers in trigonometric forms.
What is trigonometric form?
The trigonometric form of complex numbers is also called the polar form of complex numbers. Because of this, make sure to review your knowledge of polar forms.
The trigonometric form of a complex number contains the modulus, $r$, and the argument, $\theta$, representing the complex number. The general trigonometric form of complex numbers is $r(\cos \theta + i\sin \theta)$.
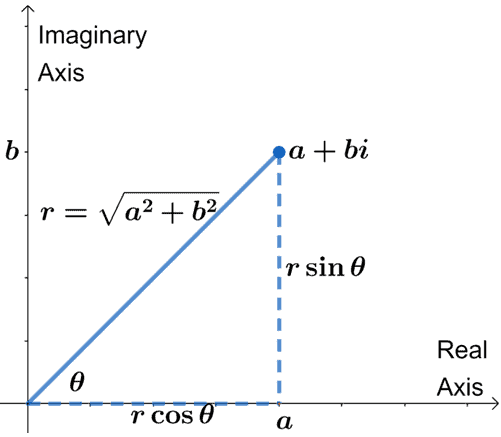
From the graph, we can see how the trigonometric or polar forms of complex numbers were derived. Since $a = r \cos\theta$ and $b = r \sin \theta$, $a + bi = r(\cos \theta + i\sin \theta)$.
From this, $r$ represents the modulus and $\theta$ shows the angle (or the argument) formed by $r$ and the real axis.
These two are the important components when presenting complex numbers in trigonometric form.
How to write complex numbers in trigonometric form?
As a refresher, the distance between the origin and the complex number is equal to $|a + bi| = \sqrt{a^2 + b^2}$. This is called the complex number’s absolute value or its modulus.
We also use this when writing the complex numbers in trigonometric form. This returns the value of $r$. Hence, we have $r = \sqrt{a^2 + b^2}$.
The graph above shows that we can also find $\theta$ using the values of $a$ and $b$. We can use the fact that $\tan \theta = \dfrac{b}{a}$, so $\theta = \tan^{-1} \dfrac{b}{a}$.
Use these two values to write $a + bi$ in trigonometric form: $r(\cos \theta + i\sin \theta)$.
Why don’t we apply what we just learned to convert $3 + 3\sqrt{3}i$ in polar form?
| $\boldsymbol{r}$ | $\boldsymbol{\theta}$ |
| $\begin{aligned}r &= \sqrt{(3)^2 + (3\sqrt{3})^2}\\&=\sqrt{9 + 27}\\&=\sqrt{36}\\&=6 \end{aligned}$ | $\begin{aligned}\tan \theta &= \dfrac{3\sqrt{3}}{3}\\\theta &= \tan^{-1} \sqrt{3}\\\theta&= 60^{\circ}, 240^{\circ}\end{aligned}$ |
Since both $3$ and $3\sqrt{3}$ are positive, we expect the argument or $\theta$ to lie on the first quadrant, so $\theta$ must be $60^{\circ}$.
This means that $3 + 3\sqrt{3}i = 6(\cos 60^{\circ} + \sin 60^{\circ})$ in polar or trigonometric form.
We can use a similar process when writing other complex numbers in their respective trigonometric forms, so make sure to try out the example above yourself?
How to multiply and divide complex numbers in trigonometric form?
We can also multiply and divide complex numbers in trigonometric form. Let’s say we have two complex numbers, $z_1 = r_1(\cos \theta_1 + i\sin \theta_1)$ and $z_2 = r_2(\cos \theta_2 + i\sin \theta_2)$, we can find their product by :
- Multiplying the moduli, $r_1$ and $r_2$.
- Finding the cosine and sine of $\theta_1 + \theta_2$.
- Combining the two results by multiplying $r_1r_2$ to $[\cos(\theta_1 + \theta_2) + i\sin (\theta_1 + \theta_2) ].
Why don’t we derive this by multiplying the two complex numbers and using algebraic and trigonometric techniques?
- Expand the product using the FOIL method.
- Rewrite $i^2$ as $-1$.
- Use the sum properties of cosine and sine, $\cos (A +B) = \cos A \cos B – \sin A \sin B$ and $\sin (A+B) = \sin A \cos B + \cos A \sin B$.
$ \begin{aligned} [r_1(\cos \theta_ 1 + i\sin \theta_1)][r_2(\cos \theta_2 + i\sin \theta_2) ] &= (r_1r_2)[(\cos \theta_1 + i \sin \theta_1)(\cos \theta_2 + i \sin \theta_2)] \\&= (r_1r_2)[(\cos \theta_1\cos \theta_2) + (\cos \theta_1i\sin\theta_2) + (i\sin\theta_1\cos \theta_2)+ (i\sin \theta_1 i \sin \theta_2)]\\&= (r_1r_2)[(\cos \theta_1\cos \theta_2) + (\cos \theta_1i\sin\theta_2) + (i\sin\theta_1\cos \theta_2)+ (i^2\sin \theta_1 \sin \theta_2)]\\&= (r_1r_2)[(\cos \theta_1\cos \theta_2) + (\cos \theta_1i\sin\theta_2) + (i\sin\theta_1\cos \theta_2)+ -\sin \theta_1 \sin \theta_2] \\&=(r_1r_2)[(\cos \theta_1\cos \theta_2-\sin \theta_1 \sin \theta_2) + i(\cos \theta_1\sin\theta_2 + \sin\theta_1\cos \theta_2) ]\\&=(r_1r_2)[\cos(\theta_1 + \theta_2) + i(\cos \theta_1\sin\theta_2 + \sin\theta_1\cos \theta_2) \\&=(r_1r_2)[(\cos \theta_1\cos \theta_2-\sin \theta_1 \sin \theta_2) + i \sin (\theta_1 + \theta_2) ] \end{aligned}$
We can apply a similar process to derive the formula for the quotient of $z_1$ and $z_2$. But, we’ll leave that for you to try out yourself. (Clue: use the FOIL method and difference properties of sine and cosine).
For now, we have $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} [\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2)]$.
This means that there is no need to convert a complex number in the trigonometric form to standard form for us to find their product or quotient.
Summary of trigonometric form definition and properties
Why don’t we summarize what we’ve learned so far about complex numbers in trigonometric form?
First, let’s recall how we can write $a + bi$ and its components in trigonometric form.
| Standard Form | Trigonometric Form |
| $\begin{aligned}\phantom{xxxx} a + bi\\ |a+bi| &= \sqrt{a^2 + b^2}\end{aligned}$ | $\begin{aligned}r(\cos \theta + i \sin \theta)\\r=\sqrt{a^2 + b^2}\\\theta= \tan^{-1} \dfrac{b}{a}\phantom{x}\end{aligned}$ |
We’ve also learned how to multiply and divide two complex numbers in trigonometric form. Given two complex numbers, $z_1 = r_1(\cos \theta_1 + i\sin \theta_1)$ and $z_2 = r_2(\cos \theta_2+ i\sin \theta_2)$, the product and quotient are as shown below:
- $z_1 z_2 = r_1r_2 [\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)]$
- $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} [\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2)]$
Let’s use these properties to solve some of the examples shown below. Make sure to review our summary section whenever you feel stuck on an item!
Example 1
Graph the following complex numbers on a complex plane, then find their respective moduli and argument.
a. $-4 + 4i$
b. $6i$
c. $4\sqrt{3} – 4i$
Solution
Let’s graph the three complex numbers on one complex plane.
- For $-4 + 4i$, graph the coordinate $(-4, 4)$ or $4$ units to the left and above the imaginary and real axes, respectively.
- Since $6i = 0 + 6i$, graph the coordinate $(0, 6)$ on the imaginary axis.
- Meanwhile $4\sqrt{3} – 4i$ can be plotted as a coordinate $(4\sqrt{3}, 4)$ on the complex plane.
Hence, we have the three complex numbers graphed in one complex plane.
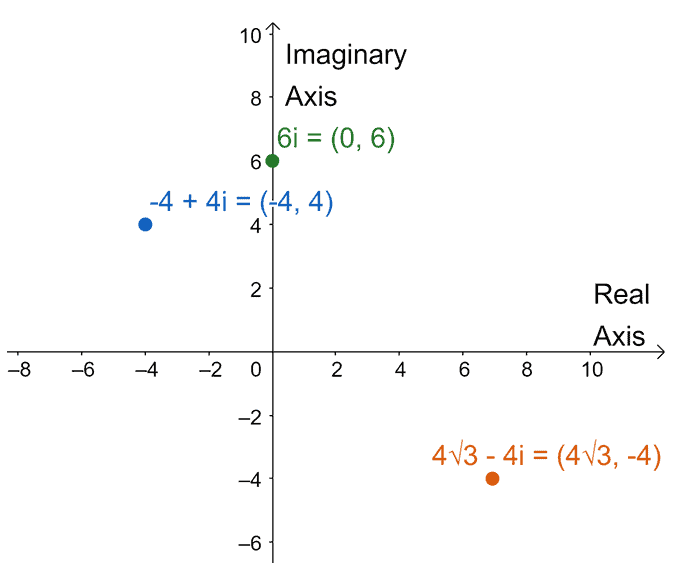
We can find each of their moduli using the formula, $r= \sqrt{a^2 + b^2}$, where $a$ is real part and $b$ is the imaginary part.
| $\boldsymbol{a + bi}$ | $\boldsymbol{r = \sqrt{a^2 + b^2}}$ |
| $-4 + 4i$ | $\sqrt{(-4)^2 + 4^2} = 4\sqrt{2}$ |
| $6i$ | $\sqrt{0^2 + 6^2} = 6$ |
| $4\sqrt{3} – 4i$ | $\sqrt{(4\sqrt{3})^2 + (-4)^2} =8$ |
We can then find the arguments (or $\theta$) for the three complex numbers and we can use the graph above to determine the right value of $\theta$ to choose.
| $\boldsymbol{a + bi}$ | $\boldsymbol{\theta = \tan^{-1} \dfrac{b}{a}}$ |
| $-4 + 4i$ | $\theta = \tan^{-1} \dfrac{4}{-4} = 135^{\circ} $ |
| $4\sqrt{3} – 4i$ | $\theta = \tan^{-1} \dfrac{-4}{4\sqrt{3}} = 330^{\circ} $ |
However, for $6i$, we can inspect its position since it lies on the upper part of the imaginary axis, $\theta = \dfrac{\pi}{2}$.
Example 2
Three complex numbers are graphed on a complex plane, as shown below.
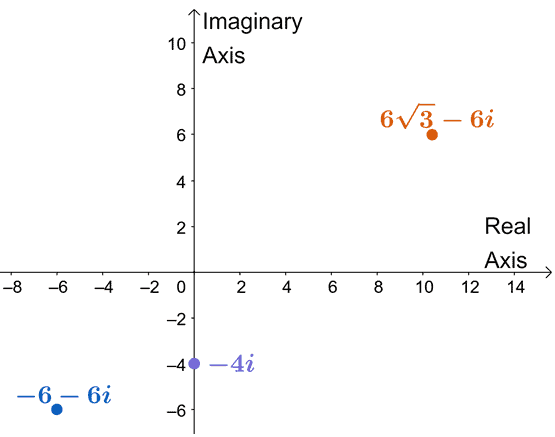
Write each complex number in trigonometric form.
Solution
We can find the moduli, $r$, of each of the complex numbers using $r = \sqrt{a^2 + b^2}$. Meanwhile, the argument or $\theta$ can be determined by taking the tangent inverse of $\dfrac{b}{a}$.
We normally end up with two values for $\theta$, so the complex numbers’ position will determine the right $\theta$ for the given.
Why don’t we go ahead and calculate the moduli for each complex number?
| $\boldsymbol{a + bi}$ | $\boldsymbol{r = \sqrt{a^2 + b^2}}$ |
| $-6 – 6i$ | $\sqrt{(-6)^2 + (-6)^2} = 6\sqrt{2}$ |
| $-4i$ | $\sqrt{0^2 + (-4)^2} = 4$ |
| $6\sqrt{3} – 6i$ | $\sqrt{(6\sqrt{3})^2 + (-6)^2} =12$ |
We now determine the argument or $\theta$ for each complex number. Make sure to check the position from the complex plane to choose the right quadrants.
| $\boldsymbol{a + bi}$ | $\boldsymbol{\theta = \tan^{-1} \dfrac{b}{a}}$ |
| $-6 – 6i$ | $\theta = \tan^{-1} \dfrac{-6}{-6} = 225^{\circ} $ |
| $6\sqrt{3} – 6i$ | $\theta = \tan^{-1} \dfrac{6\sqrt{3}}{-6} = 300^{\circ} $ |
For $-4i$, from inspection alone, we can see that $\theta = 270^{\circ}$.
We can now use these to write each complex number in trigonometric form. We simply substitute the designated values of $r$ and $\theta$ into $r(\cos \theta + i\sin \theta)$.
Hence, we have the following complex numbers in trigonometric form.
a. $-6 – 6i = 6\sqrt{2} (\cos 225^{\circ} + i \sin 225^{\circ})$
b. $- 4i = -4(\cos 270^{\circ} + i \sin 270^{\circ})$
c. $6\sqrt{3} – 6i = 12 (\cos 300^{\circ} + i \sin 300^{\circ})$
Example 3
Evaluate the following operations involving $z_1 = -3(\cos 50^{\circ} + i\sin 50^{\circ})$ and $z_2 = 6 (\cos 30^{\circ} + i\sin 30^{\circ})$.
a. $z_1 \cdot z_2$
b. $ \dfrac{z_1}{z_2}$
Solution
To find the product of $z_1$ and $z_2$, we multiply their respective moduli and find the cosine and sine of their arguments’ sum.
- The moduli, $-3$ and $6$ will have a product of $-18$.
- We also have $\cos (50^{\circ} + 30^{\circ})$ and $\sin (50^{\circ} + 30^{\circ})$.
Hence, $z_1z_2 = -18(\cos 80^{\circ} + i \sin 80^{\circ})$.
We apply a similar process to find the quotient of $z_2$ and $z_1$. But this time, we’ll need the quotient of their moduli and the difference between their arguments as shown below.
$\begin{aligned}\dfrac{z_2}{z_1} &= \dfrac{-3}{6} [\cos(50^{\circ} – 30^{\circ}) + i \sin(50^{\circ} – 30^{\circ})]\\&=-\dfrac{1}{2} (\cos 20^{\circ} + i\sin 20^{\circ})\end{aligned}$
Practice Questions
![]()
Open Problems
Graph the following complex numbers on a complex plane then find their respective moduli and argument.
a. $-6 + 6i$
b. $-9i$
c. $-4\sqrt{3} + 4i$
Open Problem Solutions

a. $r = 6\sqrt{2}$, $\theta = 315^{\circ}$
b. $r = 9$, $\theta = 270^{\circ}$
c. $r = 8$, $\theta = 330^{\circ}$
Images/mathematical drawings are created with GeoGebra.
