Trigonometric Functions – Explanation & Examples

Trigonometric functions define the connection between the legs and corresponding angles of a right triangle. There are six basic trigonometric functions — sine, cosine, tangent, cosecant, secant, and cotangent. The measures of angles are the argument values for trigonometric functions. The return values of these trigonometric functions are the real numbers.

Trigonometric functions can be defined by determining the ratios between pairs of sides of a right triangle. Trigonometric functions are used to determine the unknown side or angle of a right triangle.

After studying this lesson, we are expected to learn the concepts driven by these questions and be qualified to address accurate, specific, and consistent answers to these questions.

• What are the trigonometric functions?
• How can we determine the trigonometric ratios from the hypotenuse, adjacent, and opposite sides of a right triangle?
• How can we solve actual problems using trigonometric functions?

The goal of this lesson is to clear up any confusion you might have about the concepts involving trigonometric functions.

What is trigonometry?

In Greek, ‘trigonon’ (means triangle) and ‘metron’ (means measure). Trigonometry is simply the study of triangles — the measure of lengths and corresponding angles. That’s it!

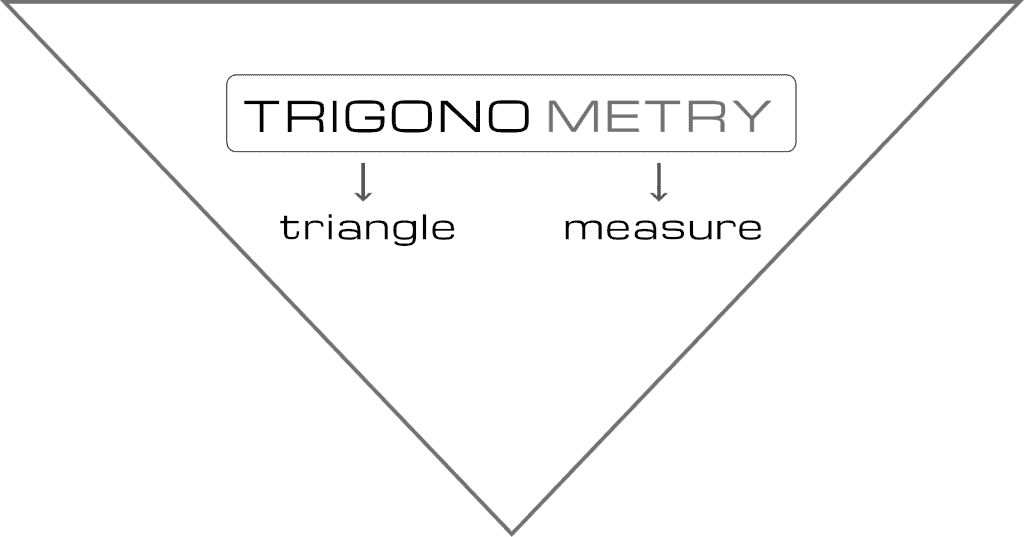Trigonometry is one of the most worrying concepts in Mathematics, but it is easy and interesting in reality.

Let us consider a triangle $ABC$ shown in figure $2.1$. Let $a$ be the length of the leg opposite angle $A$. Similarly, let $b$ and $c$ be the lengths of the legs opposite Angle $B$ and $C$, respectively.

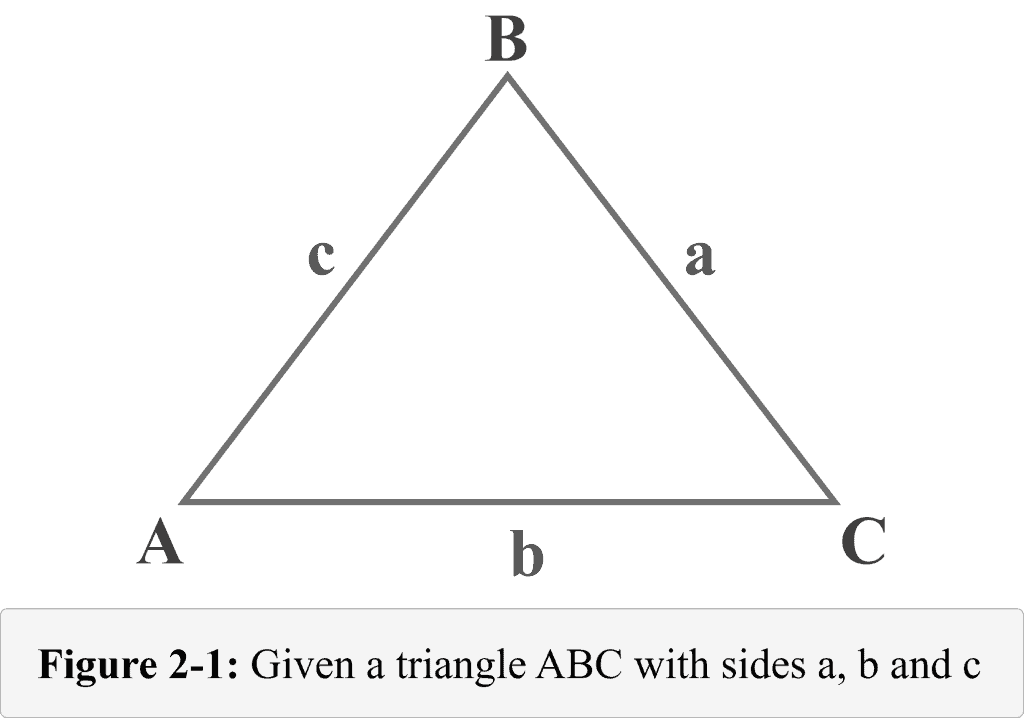
Look carefully at the triangle. What are the potential measures of this triangle?

We can determine:

The angles: $∠A$, $∠B$, and $∠C$

Or

The lengths of the sides: $a$, $b$ and $c$

These form a set of six parameters — three sides and three angles — we normally deal with in trigonometry.

A few are given and using trigonometry, we need to determine the unknowns. It is not even difficult. It is not very tricky. It is easy as trigonometry normally deals with only one type of triangle — a right triangle. This is why a right triangle is considered one of the most significant figures in Mathematics. And the good news is that you are already familiar with it.

Let us have a look at the right triangle with angle $\theta$ as shown in figure $2.2$. The tiny square with one of the angles shows that it is a right angle.

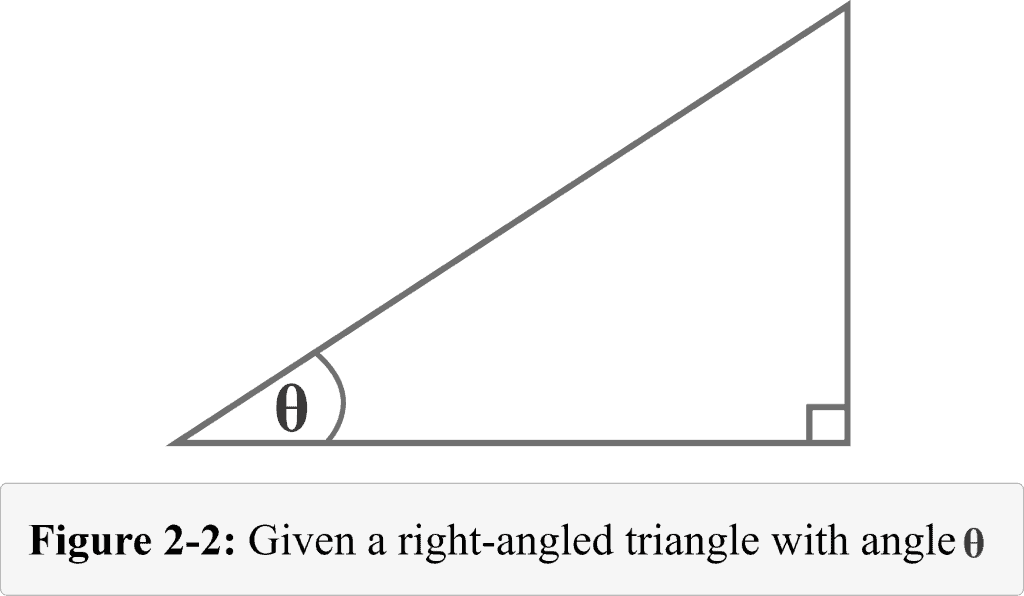
This is the triangle we will frequently be dealing with to cover most of the concepts in trigonometry.

What are trigonometric functions?

In Trigonometry, we generally deal with several trigonometric functions, but very few get what a function is. It’s easy. A function is like a box machine with two open ends, as shown in Figure 2-3. It receives an input; some process takes place inside, and it returns an output based on the process that happens inside. It all depends on what happens inside.

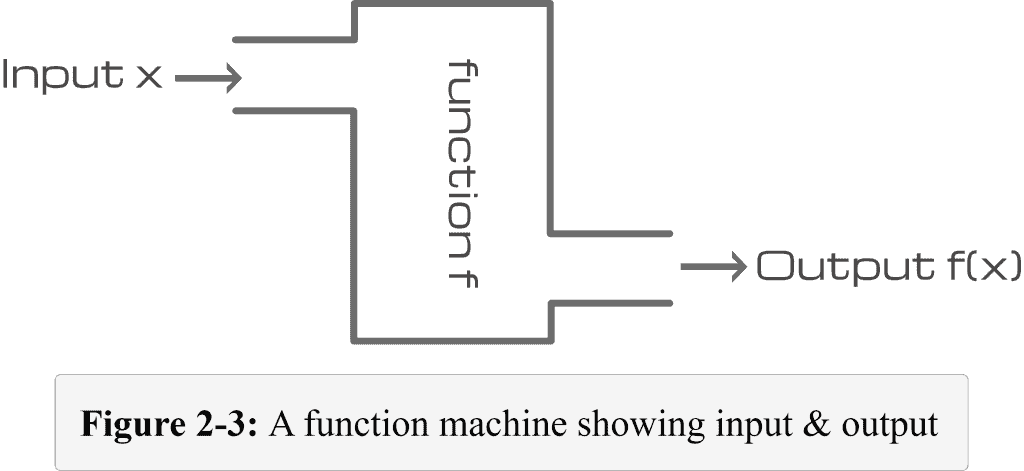
Let us consider this as our function machine, and the process it does inside is that it adds every input to $7$ and generates an output. Suppose this machine receives $3$ as input. It will add $3$ to $7$ and returns an output of $10$.

Thus, the function will be

$f(x) = x + 7$

now substitute input $x = 7$

$f (3) = 3 + 7 = 10$

Thus, the output of our function machine will be $10$.

In trigonometry, these functions are provided different names, which we will discuss here. In trigonometry, we normally — and frequently — deal with three main functions, which are sine, cosine, and tangent. These names may sound frightening initially but trust me, you will get used to it in no time.

Let us consider this box machine as a sine function, as shown in Figure 2-4. Let us say it receives a random value $\theta$. It does some process inside to return some value.

What could be the value? What could be the process? That depends totally on the triangle.

Figure 2-5 shows a right-angled triangle with the hypotenuse, adjacent, and opposite sides with respect to the reference angle.

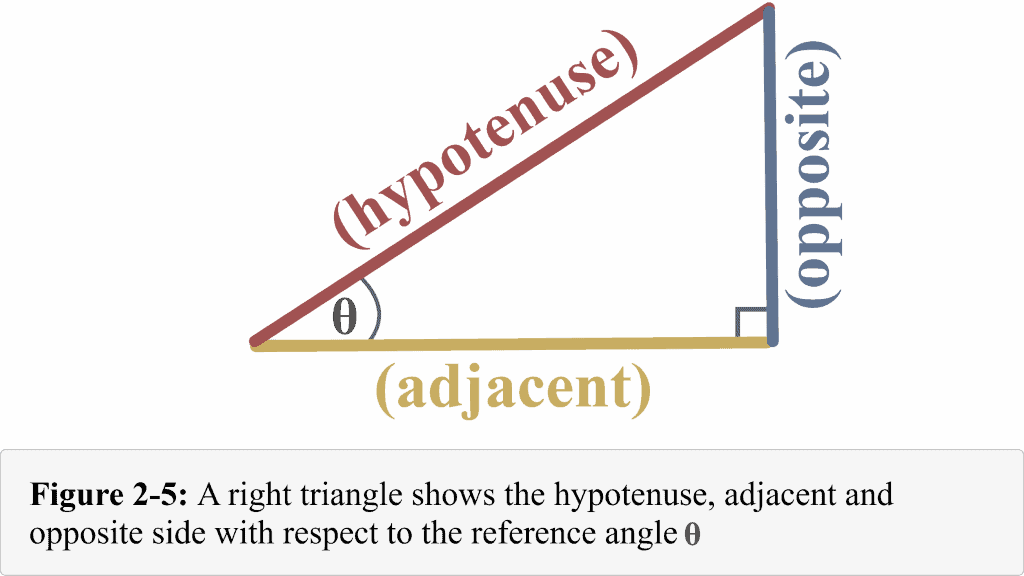
Looking at the diagram, it is clear that:

• The adjacent side is right next to the reference angle $\theta$.
• The opposite side lies exactly opposite the reference angle $\theta$.
• Hypotenuse — the longest side — of a right-angled triangle is opposite to the right angle.

Now using Figure 2-5, we can easily determine the sine function.

Sine of angle $\theta$ is written as $\sin \theta$.

Remember that $\sin \theta$ is equal to the opposite divided by the hypotenuse.

Thus, the formula of sine function will be:

And what about the cosine function?

Cosine of angle $\theta$ is written as $\cos \theta$.

Remember that $\cos \theta$ is equal to the ratio of the length of the adjacent side to $\theta$ to the length of the hypotenuse.

Thus, the formula of cosine function will be:

The next very important function is the tangent function.

The tangent of angle $\theta$ is written as $\tan \theta$.

Remember that $\tan \theta$ is equal to the ratio of the length of the side opposite the angle $\theta$ to the length of the side adjacent to $\theta$.

Thus, the formula of tangent function will be:

Therefore, the ratios we have generated are known as sine, cosine, and tangent and are termed as trigonometric functions.

How to remember the formulae of the main trigonometric functions?

To remember the formulae of the trigonometric functions, just memorize one code word:

SOH – CAH – TOA

Check how easy it gets.

Reciprocal trigonometric functions

If we just flip the three trigonometric ratios we already determined, we can find three more trigonometric functions — reciprocal trigonometric functions — by applying a little algebra. 

The cosecant of angle $\theta$ is written as $\csc \theta$.

Remember that $\csc \theta$ is the reciprocal of $\sin \theta$.

${\displaystyle \csc \theta = {\frac {1}{\sin \theta}}}$

As

${\displaystyle \sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

Thus, the formula of cosecant function will be:

Similarly,

The secant of angle $\theta$ is written as $\sec \theta$.

$\sec \theta$ is the reciprocal of $\cos \theta$.

${\displaystyle \sec \theta = {\frac {1}{\cos \theta}}}$

As

${\displaystyle \cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

Thus, the formula of secant function will be:

Similarly,

The cotangent of angle $\theta$ is written as $\cot \theta$.

$\cot \theta$ is the reciprocal of $\tan \theta$.

${\displaystyle \cot \theta = {\frac {1}{\tan \theta}}}$

As

${\displaystyle \tan A ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

Thus, the formula of cotangent function will be:

Therefore, the latest ratios we have generated are known as cosecant, secant, and tangent and are also termed as (reciprocal) trigonometric functions.

The summary of the results is in the table below:

Each of these legs will have a length. Thus, these trigonometric functions will return a numerical value.

Example 1

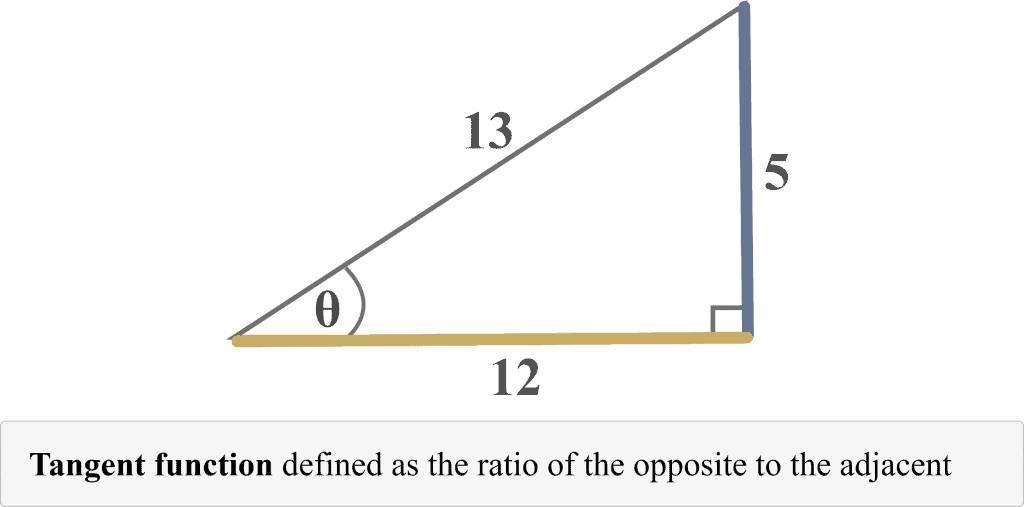
Let us consider having a right triangle with sides of length $12$ and $5$ and hypotenuse of length $13$. Let $\theta$ be the angle opposite the side of length $5$ as shown in the Figure below. What is:

1. sine $\theta$
2. cosine $\theta$
3. tangent $\theta$

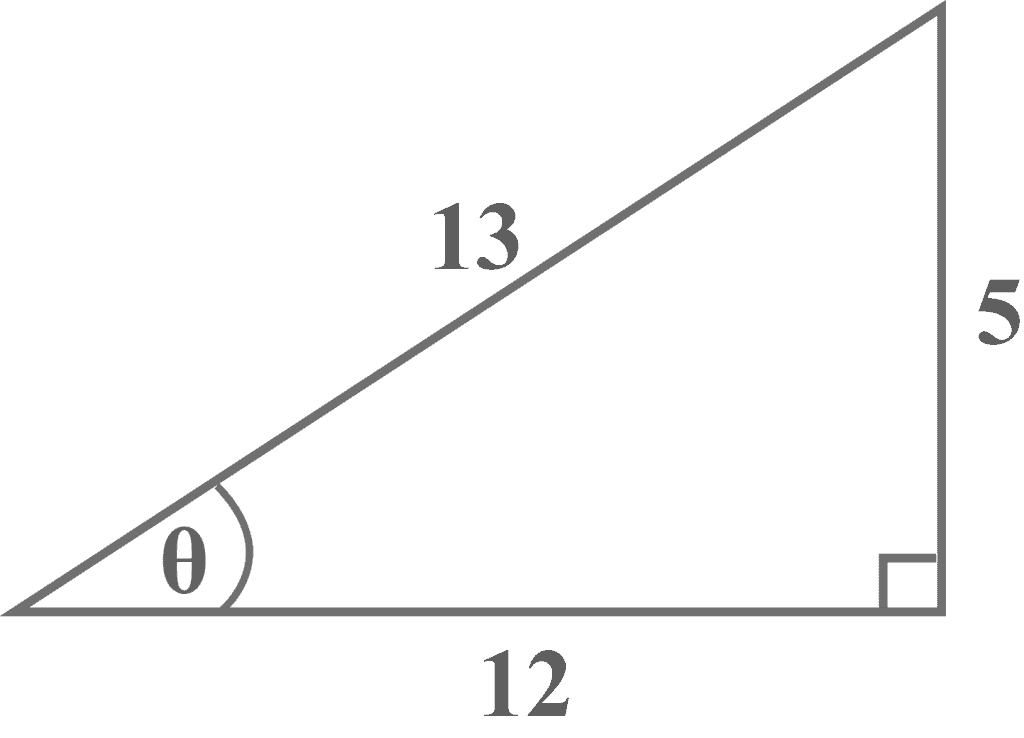
Solution:

Part a) Determining $\sin \theta$

Looking at the diagram, it is clear that the side of length $5$ is the opposite side that lies exactly opposite the reference angle $\theta$, and the side of length $13$ is the hypotenuse. Thus,

Opposite = $5$

Hypotenuse = $13$

We know that formula of the sine function is

${\displaystyle \sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

Thus,

${\displaystyle \sin \theta ={\frac {5}{13}}}$

The diagram of $\sin \theta$ is also shown below.

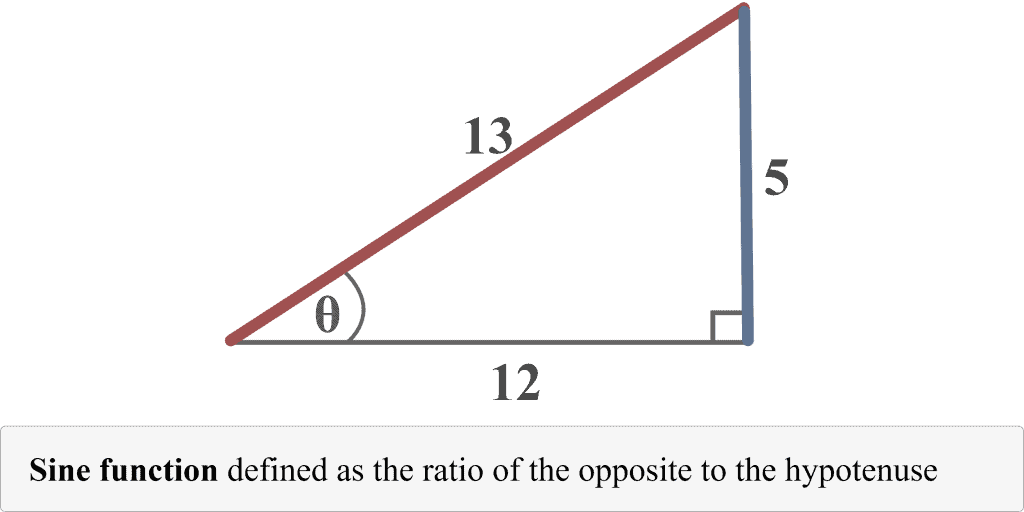
Part b) Determining $\cos \theta$

Looking at the diagram, it is clear that the side of length $12$ is right next to the reference angle $\theta$, and the side of length $13%%EDITORCONTENT%%nbsp;is the hypotenuse. Thus,

Adjacent =$12$

Hypotenuse =$13$

We know that formula of the cosine function is

${\displaystyle \cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

Thus,

${\displaystyle \cos \theta ={\frac {12}{13}}}$

The diagram of $\cos \theta$ is also shown below.

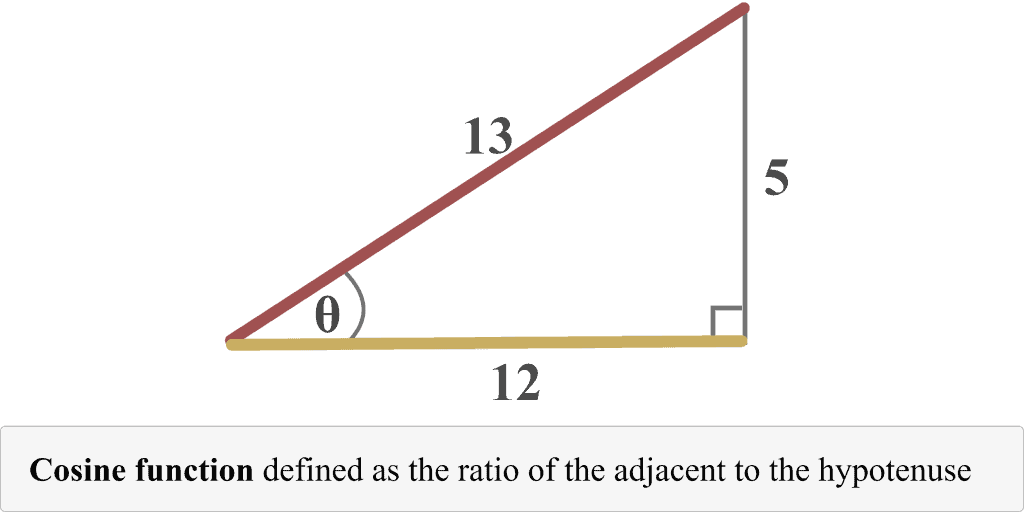
Part c) Determining $\tan \theta$

Looking at the diagram, it is clear that:

Opposite = $5$

Adjacent = $12$

We know that formula of the tangent function is

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

Thus,

${\displaystyle \tan \theta ={\frac {5}{12}}}$

The diagram of $\tan \theta$ is also shown below.

Example 2

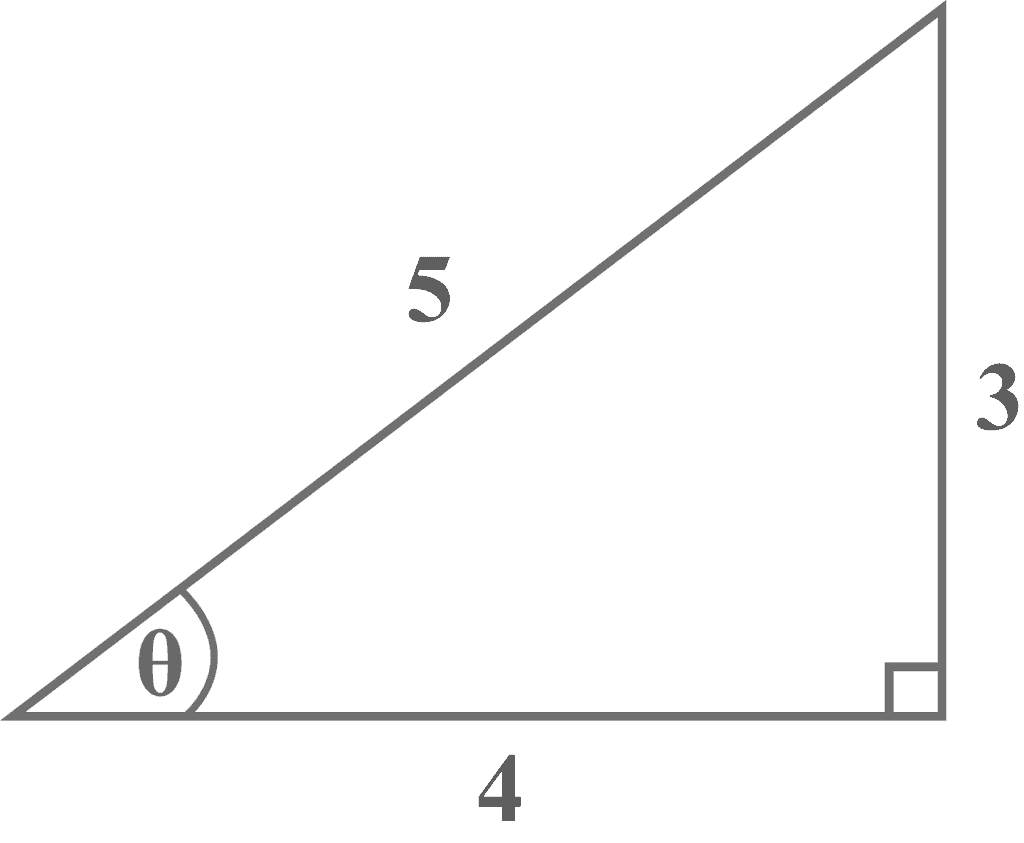
Let us consider having a right triangle with sides of length $4$ and $3$ and hypotenuse of length $5$. Let $\theta$ be the angle opposite the side of length $3$ as shown in the Figure below. What is:

1. $\csc \theta$
2. $\sec \theta$
3. $\cot \theta$

Solution:

Part a) Determining $\csc \theta$

Looking at the diagram, it is clear that the side of length $3$ is the opposite side that lies exactly opposite the reference angle $\theta$, and the side of length $5%%EDITORCONTENT%%nbsp;is the hypotenuse. Thus,

Opposite = $3$

Hypotenuse = $5$

We know that formula of the cosecant function is

${\displaystyle \csc \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}$

Thus,

${\displaystyle \csc \theta ={\frac {5}{3}}}$

Part b) Determining $\sec \theta$

Looking at the diagram, we can determine that the side of length $4$ is right next to the reference angle $\theta$. Thus,

Adjacent = $4$

Hypotenuse = $5$

We know that formula of the secant function is

${\displaystyle \sec \theta ={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}}$

Thus,

${\displaystyle \sec \theta ={\frac {5}{4}}}$

Part c) Determining $\cot \theta$

Looking at the diagram, we can check that:

Adjacent = $4$

Opposite = $3$

We know that formula of the cotangent function is

${\displaystyle \cot \theta ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}}$

Thus,

${\displaystyle \cot \theta ={\frac {4}{3}}}$

Example 3

Given a right triangle with sides of length $11$ and $7$. Which option represents the trigonometric ratio of ${\frac {7}{11}}$?

       a) $\sin \theta$

       b) $\cos \theta$

       c) $\tan \theta$

       d) $\cot \theta$

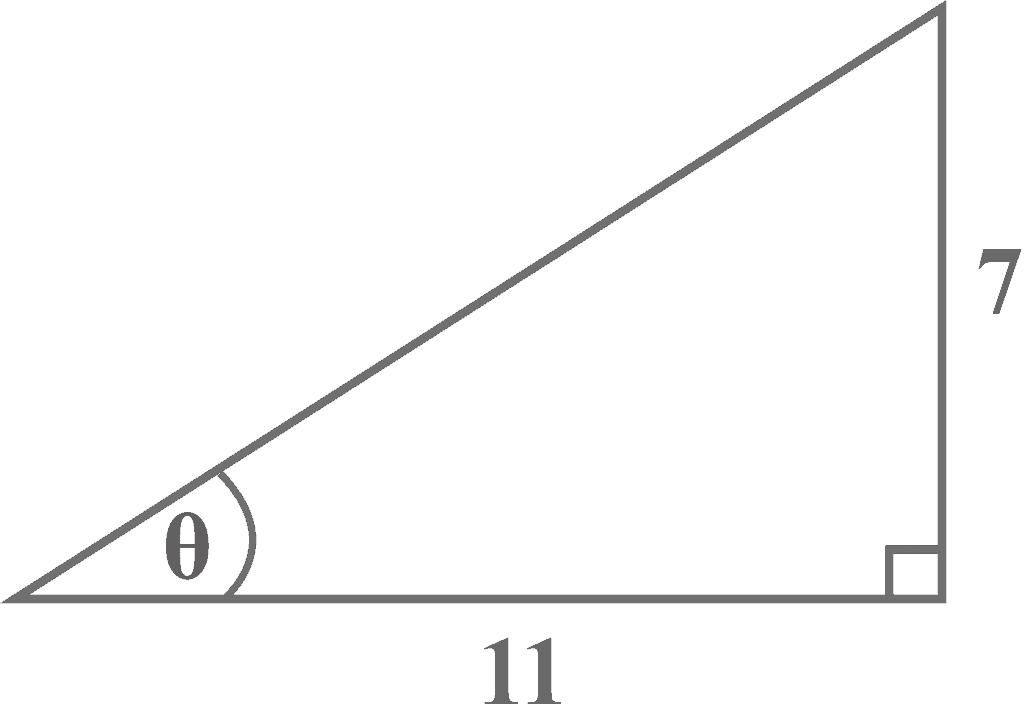
Look at the diagram. It is clear that the side of length $7$ is the opposite side that lies exactly opposite the reference angle $\theta$, and the side of length $11%%EDITORCONTENT%%nbsp;is right next to the reference angle. Thus,

Opposite = $7$

Adjacent = $11$

We know that formula of the tangent function is

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

Thus,

${\displaystyle \tan \theta ={\frac {7}{11}}}$

Therefore, Option c) is the true choice.