Trigonometric Special Angles – Explanation & Examples

We normally need to use the calculator to figure out the values of the trigonometric functions of an angle unless we are dealing with trigonometric special angles. Because it is not possible to precisely evaluate the trigonometric functions for most of the angles. But is it true for all the angles? The answer is no — not always.

Trigonometric special angles — 30^o, 45^o, and 60^o — generate rather straightforward trigonometric values. We can precisely evaluate the trigonometric functions for these special angles without a calculator. 

 After studying this lesson, we are expected to learn the concepts driven by these questions and be qualified to address accurate, specific, and consistent answers to these questions.

• What are trigonometric special angles?
• How to solve trigonometric special angles?
• How can we solve actual problems using trigonometric special angles?

The goal of this lesson is to clear up any confusion you might have about the concepts involving trigonometric special angles.

What are trigonometric special angles?

There are specific angles that provide simple and exact trigonometric values. These specific angles are known as trigonometric special angles. These are 30^o, 45^o, and 60^o.

What is so special about them?

Because it is easy to ‘exactly’ evaluate the trigonometric function without using a calculator for these angles. These angles have comparatively clean values, offering us a great deal to solve Math problems. We use these values to give precise answers for determining the values of many trigonometric ratios.

We will use two ‘special right triangles’ to discuss the special angels in this lesson.

1. 45^o – 45^o – 90^o triangle — also known as isosceles triangle — is a special triangle with the angles 45^o, 45^o, and 90^o.
2. 30^o – 60^o – 90^o triangle is another special triangle with the angles 30^o, 60^o, and 90^o.

These special triangles have a unique ability to provide us precise and simple answers when dealing with trigonometric functions.

The good thing is that you are already familiarized with these special triangles as we have discussed them in our Geometry lessons. We will just use them to solve trigonometric special angles and determine the trigonometric ratios of these special angles.

How to solve trigonometric special angles?

Case 1:

Special angle 45^o (from a 45^o – 45^o – 90^o triangle)

The following figure 7-1 represents a $45^{\circ }$ – $45^{\circ }$ – $90^{\circ }$ isosceles right triangle with two $45^{\circ }$ degree angles. The lengths of the three legs of the right triangle are named $a$, $b$, and $c$. The angles opposite the legs of lengths $a$, $b$, and $c$ are named $A$, $B$, and $C$. The tiny square with the angle $C$ shows that it is a right angle.

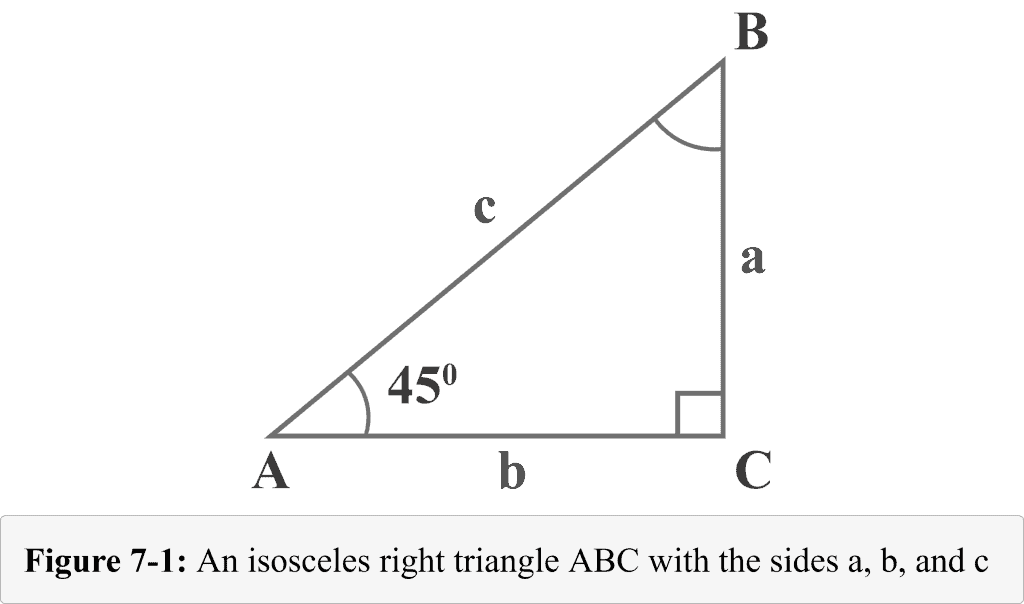
Looking at diagram 7-1, the measure of angle $A$ is $45^{\circ }$. Since the sum of angles in a triangle is $180^{\circ }$, the measure of angle $B$ would also be $45^{\circ }$.

As values of trigonometric functions are based on the angle and not on the size of the triangle. For simplicity, we take:

$a = 1$

$b = 1$

In this case the triangle will be isosceles triangle. We can simply determine the hypotenuse using Pythagorean theorem.

$c^{2}=a^{2}+b^{2}$

substitute $a = 1$, $b = 1$ in the formula

$c^{2}=1^{2}+1^{2}$

$c^{2}= 2$

$c = \sqrt{2}$

The following figure 7-2 shows that the isosceles triangle has two equal sides ($a = b = 1$), hypotenuse ($c = \sqrt{2}$), and equal base angles ($45^{\circ }$ and $45^{\circ }$).

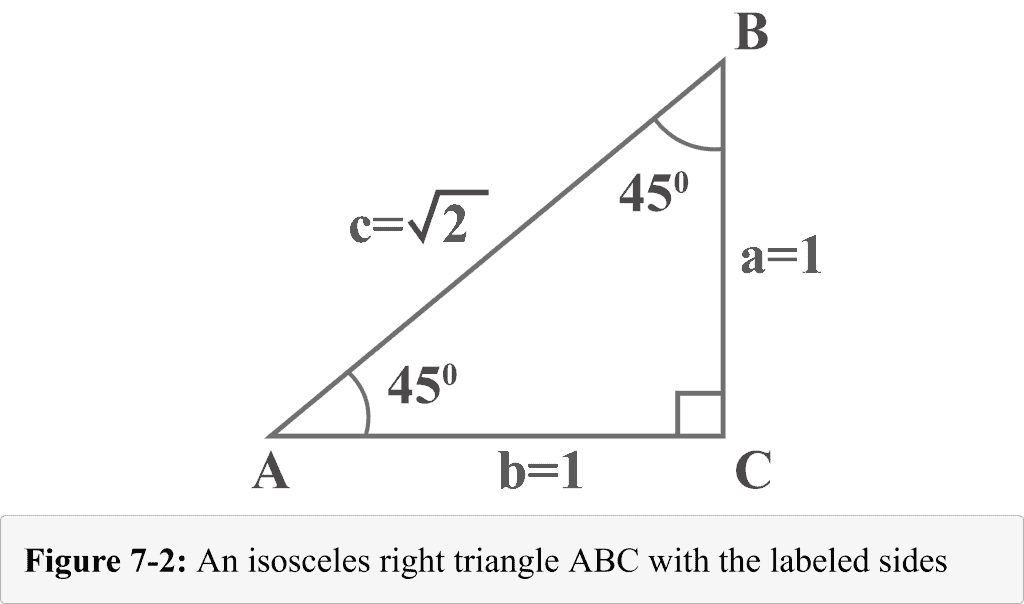
When m ∠ A = 45^o:

We can easily determine the values of trigonometric ratio for $45^{\circ }$.

Looking at diagram 7-2 from the perspective of m ∠ A = 45^o

Sine function

Sine function is the ratio of the opposite side to the hypotenuse.

${\displaystyle \sin 45^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

${\displaystyle \sin 45^{\circ } ={\frac {a}{c}}}$

substitute $a = 1$, $c = \sqrt{2}$ 

Cosine function

Cosine function is the ratio of the adjacent side to the hypotenuse.

Thus,

${\displaystyle \cos 45^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

${\displaystyle \cos 45^{\circ } ={\frac {b}{c}}}$

substitute $b = 1$, $c = \sqrt{2}$ 

Tangent function

Tangent function is the ratio of the opposite side to the adjacent side.

Thus,

${\displaystyle \tan 45^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

${\displaystyle \tan 45^{\circ } ={\frac {a}{b}}}$

substitute $a = 1$, $b = 1$ 

${\displaystyle \tan 45^{\circ } ={\frac {1}{1}}}$

Cosecant function

Cosecant function is the ratio of the hypotenuse to the opposite side.

Thus,

${\displaystyle \csc 45^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}$

${\displaystyle \csc 45^{\circ } ={\frac {c}{a}}}$

substitute $c = \sqrt{2}$, $a = 1$ 

${\displaystyle \csc 45^{\circ } ={\frac { \sqrt{2}}{1}}}$

Secant function

Secant function is the ratio of the hypotenuse to the adjacent side.

Thus,

${\displaystyle \sec 45^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}}$

${\displaystyle \sec 45^{\circ } ={\frac {c}{b}}}$

substitute $c = \sqrt{2}$, $b = 1$ 

${\displaystyle \sec 45^{\circ } ={\frac { \sqrt{2}}{1}}}$

Cotangent function

Cotangent function is the ratio of the adjacent side to the opposite side.

Thus,

${\displaystyle \cot 45^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}}$

${\displaystyle \cot 45^{\circ } ={\frac {b}{a}}}$

substitute $b = 1$, $a = 1$ 

${\displaystyle \cot 45^{\circ } ={\frac {1}{1}}}$

Case 2:

Special angles 30^o and 60^o (from a 30^o – 60^o – 90^o triangle)

The following figure 7-3 represents an equilateral triangle with sides $a = 2$, $b = 2$, and $c =2$. Since equilateral triangle has congruent angles and the measure of angles in a triangle is $180^{\circ }$, each angle measures $60^{\circ }$.

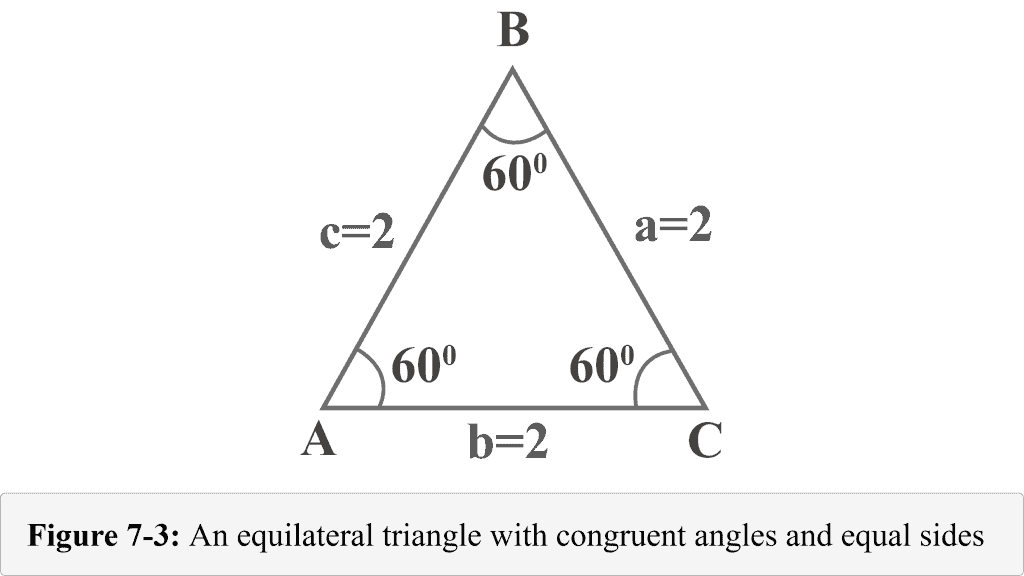
Let us draw an altitude from the vertex $B$. The altitude separates an equilateral triangle into two congruent right triangles. In Figure 7-4, ${\displaystyle {\overline {BD}}}$ is altitude, $ΔABD\:≅\:ΔCBD$, $∠BDA$ is a right angle, $m∠A=60^{\circ }$, and $m∠ABD=30^{\circ }$. 

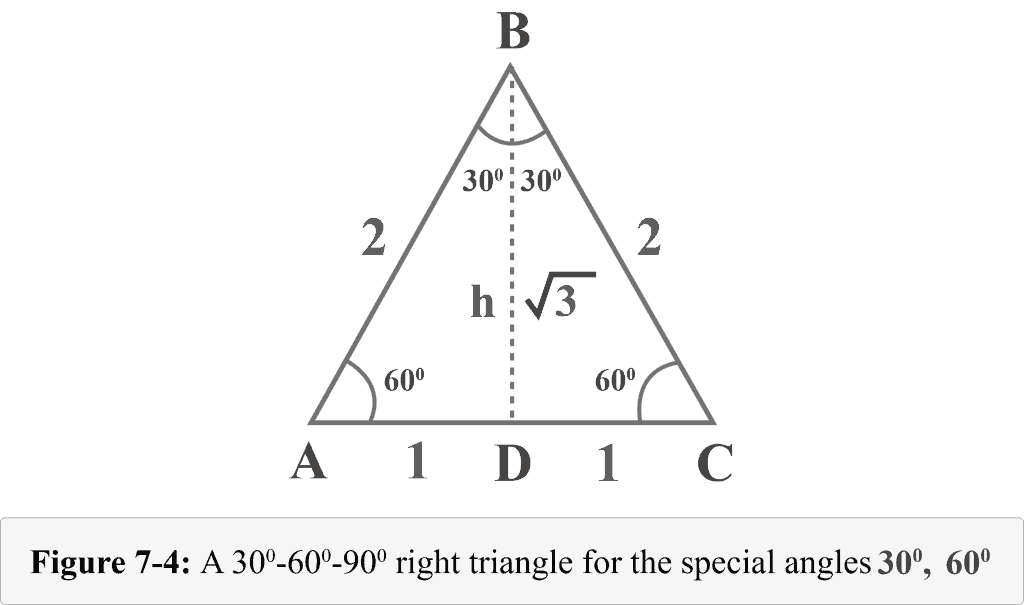
We can determine the height h of these triangles by the Pythagorean theorem.

$(AB)^{2}=(BD)^{2}+(AD)^{2}$

$(BD)^{2}=(AB)^{2} – (AD)^{2}$

Substitute $(BD) = h$, $AB = 2$, and $AD = 1$ in the formula

$h^{2}=(2)^{2} – (1)^{2}$

$h^{2}= 3$

$h = \sqrt{3}$

As the altitude $h$ splits the equilateral triangle into two congruent 30^o – 60^o – 90^o triangles. Let us knock out one of those right triangles, let suppose $ABD$, and determine the values of trigonometric ratio for $30^{\circ }$ and $60^{\circ }$.

When m ∠ B = 30^o:

The following Figure 7-5 represents the right-angled triangle from the perspective of the special angle $B = 30^{\circ }$.

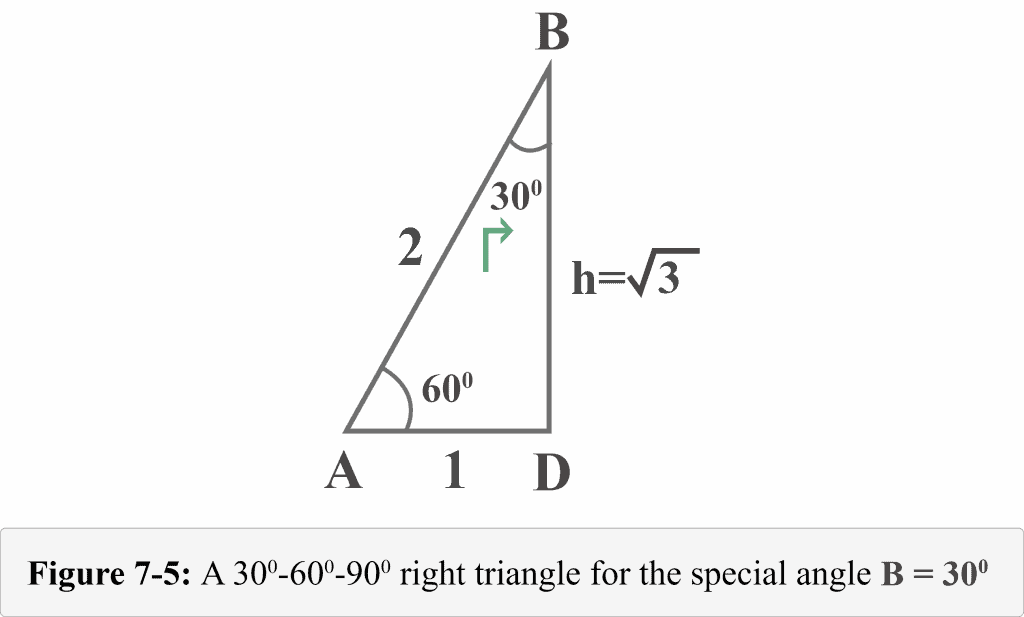
Now, we can easily determine the values of trigonometric ratio for $B = 30^{\circ }$.

Looking at the diagram 7-5 from the perspective of m ∠ B = 30^o

Sine function

${\displaystyle \sin 30^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

${\displaystyle \sin 30^{\circ } ={\frac {AD}{AB}}}$

substituting $AD = 1$ and $AB = 2$

Cosine function

${\displaystyle \cos 30^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

${\displaystyle \cos 30^{\circ } ={\frac {BD}{AB}}}$

substituting $BD = \sqrt{3}$ and $AB = 2$

Tangent function

${\displaystyle \tan 30^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

${\displaystyle \tan 30^{\circ } ={\frac {AD}{BD}}}$

substituting $AD = 1$ and $BD = \sqrt{3}$

Cosecant function

${\displaystyle \csc 30^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}$

${\displaystyle \csc 30^{\circ } ={\frac {AB}{AD}}}$

substituting $AB = 2$ and $AD = 1$

${\displaystyle \csc 30^{\circ } ={\frac {2}{1}}}$

Secant function

${\displaystyle \sec 30^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {adjacent} }}}$

${\displaystyle \sec 30^{\circ } ={\frac {AB}{BD}}}$

substituting $AB = 2$ and $BD = \sqrt{3}$

Cotangent function

${\displaystyle \cot 30^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}}$

${\displaystyle \cot 30^{\circ } ={\frac {BD}{AD}}}$

substituting $BD = \sqrt{3}$ and $AD = 1$

${\displaystyle \cot 30^{\circ } ={\frac {\sqrt{3}}{1}}}$

When m ∠ A = 60^o:

The following Figure 7-6 represents the right-angled triangle from the perspective of the special angle $A = 60^{\circ }$.

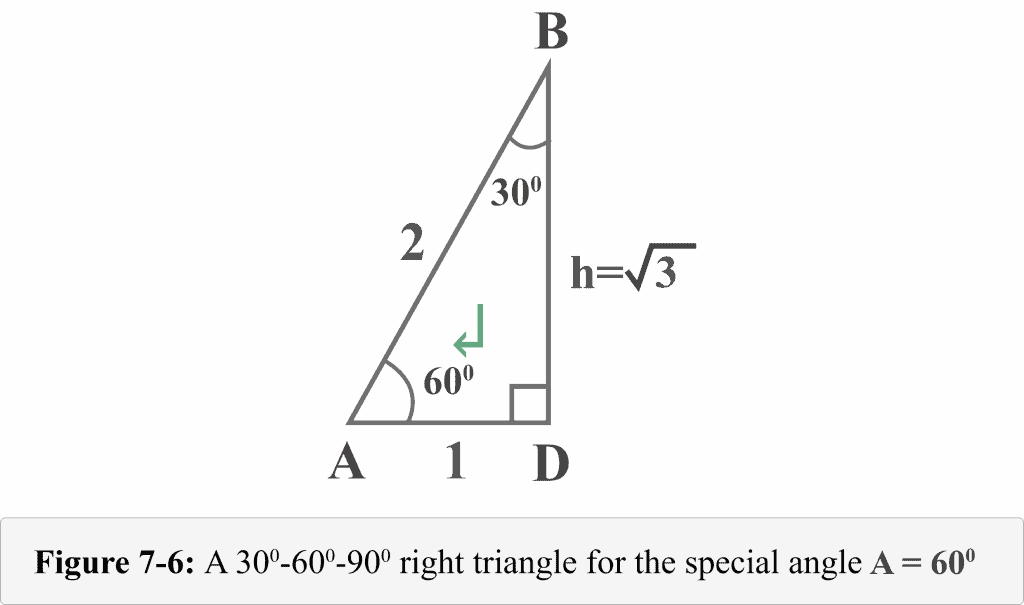
Now, we can easily determine the values of trigonometric ratio for $A = 60^{\circ }$.

Looking at the diagram 7-6 from the perspective of m ∠ A = 60^o

Sine function

${\displaystyle \sin 60^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}}$

${\displaystyle \sin 60^{\circ } ={\frac {BD}{AB}}}$

substituting $BD = \sqrt{3}$ and $AB = 2$

Cosine function

${\displaystyle \cos 60^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}}$

${\displaystyle \cos 60^{\circ } ={\frac {AD}{AB}}}$

substituting $AD = 1$ and $AB = 2$

Tangent function

${\displaystyle \tan 60^{\circ } ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

${\displaystyle \tan 60^{\circ } ={\frac {BD}{AD}}}$

substituting $BD = \sqrt{3}$ and $AD = 1$

${\displaystyle \tan 60^{\circ } ={\frac {\sqrt{3}}{1}}}$

Cosecant  function

${\displaystyle \csc 60^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {opposite} }}}$

${\displaystyle \csc 60^{\circ } ={\frac {AB}{BD}}}$

substituting  and $AB = 2$ and $BD = \sqrt{3}$

Secant function

${\displaystyle \sec 60^{\circ } ={\frac {\mathrm {hypotenuse} }{\mathrm {agjacent} }}}$

${\displaystyle \sec 60^{\circ } ={\frac {AB}{AD}}}$

substituting $AB = 2$ and $AD = 1$

Cotangent function

${\displaystyle \cot 60^{\circ } ={\frac {\mathrm {adjacent} }{\mathrm {opposite} }}}$

${\displaystyle \cot 60^{\circ } ={\frac {AD}{BD}}}$

substituting $AD = 1$ and $BD = \sqrt{3}$

Here is the complete chart for the values of trigonometric ratio for the special angles $30^{\circ }$, $45^{\circ }$, and $60^{\circ }$.

                                                                   Table 7.1

Example $1$

Find the exact value of the following trigonometric expression without using a calculator.

$\tan 30^{\circ } – \cot 60^{\circ } + \tan 45^{\circ }$

Solution:

$\tan 30^{\circ } – \cot 60^{\circ } + \tan 45^{\circ }$

Using the table,

substitute ${\displaystyle \tan 30^{\circ } ={\frac {1}{\sqrt{3}}}}$,  ${\displaystyle \cot 60^{\circ } ={\frac {1}{\sqrt{3}}}}$,  $\tan 45^{\circ }=1$

= ${\frac { 1}{\sqrt{3}}}  –  {\frac { 1}{\sqrt{3}}} + 1$

= $0 + 1$

= $1$

Example $2$

Find the exact value of the following trigonometric expression.

$4\csc 30^{\circ } + 4\tan 45^{\circ } + 7\sec 60^{\circ }$

Solution:

$4\csc 30^{\circ } + 4\tan 45^{\circ } + 7\sec 60^{\circ }$

= $4 (2) + 4 (1) + 7 (2)$

= $8 + 4 + 14$

= $26$

Example $3$

Find the exact value of the following trigonometric expression.

$2\:\left(\sin\:30^{\circ }\right)^2+\:3\:\left(\cos\:30^{\circ }\right)^2\:+\:6\:\left(\tan\:30^{\circ }\right)^2+\:2\:\left(\cot\:45^{\circ }\right)^2$

= $2\left(\frac{1}{2}\right)^2\:+\:3\:\left(\frac{\sqrt{3}}{2}\right)^2\:+\:6\:\left(\frac{1}{\sqrt{3}}\right)^2\:+2$

= $2\left(\frac{1}{4}\right)+\:3\:\left(\frac{3}{4}\right)\:+\:6\:\left(\frac{1}{3}\right)\:+2$

= $\frac{1}{2}+\frac{9}{4}+2+2$

= $\frac{1}{2}+\frac{9}{4}+4$

= $\frac{27}{4}$