- Home
- >
- Trigonometric substitution – Forms, Technique, and Examples
JUMP TO TOPIC
Trigonometric substitution – Forms, Technique, and Examples
 The trigonometric substitution method is an important technique for integral calculus. There are expressions when the earlier methods we’ve learned about integrating functions won’t apply them, so it’s important that we also learn special techniques such as the trigonometric substitution method.
The trigonometric substitution method is an important technique for integral calculus. There are expressions when the earlier methods we’ve learned about integrating functions won’t apply them, so it’s important that we also learn special techniques such as the trigonometric substitution method.
The trigonometric substitution helps us integrate expressions that contain expressions with the forms, $\boldsymbol{\sqrt{a^2 + x^2}}$, $\boldsymbol{\sqrt{a^2 – x^2}}$, and $\boldsymbol{\sqrt{x^2 + a^2}}$.
This article will show you when and how to apply the trigonometric substitution when integrating expressions will the three mentioned forms. We’ll also learn why we can use the techniques we’ll be learning in this section and see how we can integrate trigonometric substitution with our current knowledge of integrating functions.
What is a trigonometric substitution?
Trigonometric substitution is an important method in integral calculus, especially when we want to find the antiderivatives of radical expressions. The trigonometric substitution uses trigonometric identities to rewrite expressions and eventually find the given function’s antiderivative through other integration techniques.
By the end of this discussion, we’ll learn how to integrate expressions such as those shown below.
\begin{aligned}\int \sqrt{4 – x^2} dx\\\int (x – 2)^{\frac{3}{2}}dx\\\int \dfrac{\sqrt{16x^2 – 25}}{x} dx \end{aligned}
The integrals of these expressions used to be inaccessible when using the fundamental techniques we’ve learned earlier in integral calculus. Through trigonometric substitution, we’ll now be able to integrate complex radical expressions.
When to use trigonometric substitution?
The trigonometric substitution is a special method developed to integrate expressions of the forms $\boldsymbol{\sqrt{a^2 + x^2}}$, $\boldsymbol{\sqrt{a^2 – x^2}}$, and $\boldsymbol{\sqrt{x^2 + a^2}}$.
When applying the trigonometric substitution method on an expression, we want to integrate, make sure to apply the right trigonometric identity for the substitution.
This table summarizes the helpful identities we’ll need to integrate expressions using the trigonometric substitution.
| General Form | Substitution Applied | Trigonometric Identity |
| \begin{aligned}\sqrt{a^2 – x^2}\end{aligned} | \begin{aligned}x &= a\sin \theta\\\theta &\in \left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right] \end{aligned} | \begin{aligned}1 – \sin^2 \theta = \cos^2 \theta \end{aligned} |
| \begin{aligned}\sqrt{a^2 + x^2}\end{aligned} | \begin{aligned}x &= a\tan \theta\\\theta &\in \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) \end{aligned} | \begin{aligned}1 + \tan^2 \theta = \sec^2 \theta \end{aligned} |
| \begin{aligned}\sqrt{x^2 – a^2}\end{aligned} | \begin{aligned}x &= a\sec \theta\\\theta &\in \left[0, \dfrac{\pi}{2}\right) \cup \left[\pi, \dfrac{3\pi}{2}\right)\end{aligned} | \begin{aligned}\sec^2 \theta – 1 = \tan^2 \theta \end{aligned} |
Keep in mind that for the substitution, $\theta$ must be within the allowed domain for the corresponding inverse trigonometric function.
How to apply the trigonometric substitution method?
Now that we know the form and essential trigonometric identities that can help us integrate radical expressions, we must know how to apply the substitution properly.
Below are some guidelines on how to use the trigonometric identities to integrate radical expressions:
- Identify the expression and its general form in which trigonometric substitution applies.
- Substitute $x$ with the proper trigonometric function then express $dx$ in terms of $d\theta$. The equations below should guide you, and you can double-check this by refreshing your knowledge on trigonometric derivatives.
\begin{aligned}x &= a \sin \theta \rightarrow dx = a\cos \theta \phantom{x}d\theta\\x &= a \sec\theta \rightarrow dx = a\sec\theta\tan \theta \phantom{x}d\theta\\x &= a \tan \theta \rightarrow dx = a\sec^2 \theta \phantom{x}d\theta\end{aligned}
- Simplify the new expression in terms of $\theta$ and use your integral techniques to evaluate the new expression’s integral.
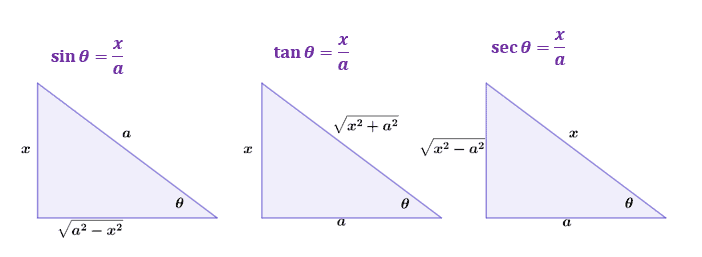
- Use the reference triangle suited for the expression to convert the integral back to $x$. Check the three reference triangles shown below as a guide for you.

The best way to master this technique is by going through different expressions, and we’ll begin with integrating an expression of the form, $\sqrt{a^2 – x^2}$. Let’s see how we can use the trigonometric substitution and the rest of the antiderivative formulas that we already know to integrate $\sqrt{1 -x^2}$.
For this case, $a^2 = 1$, so we can substitute $x$ with $(1)\sin \theta$ or $\sin \theta$ and also have $dx = \cos \phantom{x}d\theta$.
\begin{aligned}x &= \sin \theta\\x^2 &= \sin^2 \theta\\dx &= \cos \theta \phantom{x}d\theta\\\\\int \sqrt{1 – {\color{Purple}x^2}} \phantom{x}{\color{Orange}dx }&= \int \sqrt{1 – {\color{Purple}\sin^2 \theta}}{\color{Orange}\phantom{x}\cos \theta \phantom{x}d\theta } \end{aligned}
We can then use the trigonometric identity, $\sin^2 \theta + \cos^2 \theta = 1$ or $1 – \sin^2 \theta = \cos^2 \theta$, to rewrite the expression within the radical expression. We can then evaluate $\sqrt{\cos^2 \theta}$ and use the antiderivative of $\cos \theta$ to simplify the integral.
\begin{aligned}\int \sqrt{1 – {\sin^2 \theta}}{\phantom{x}\cos \theta \phantom{x}d\theta } &= \int \sqrt{\color{Purple} \cos^2 \theta}\phantom{x} \cos \theta\phantom{x}d\theta,\phantom{x}\color{Purple} 1 – \sin^2\theta = \cos^2 \theta\\&= \int |\cos \theta| \cos \theta\phantom{x}d\theta\\&= \int \cos^2 \theta\phantom{x}d\theta \end{aligned}
Keep in mind that since we have $|\cos \theta|$, we’ll have to make sure that $\theta$ is within the set interval, $\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]$. Through the double-angle formula for cosine, we have $\cos 2\theta = 2 \cos^2\theta – 1$
\begin{aligned}\int \cos^2 \theta\phantom{x}d\theta&=\int {\color{Purple}\dfrac{1 + \cos 2\theta}{2}} \phantom{x}d\theta, \phantom{x}{\color{Purple} \cos 2\theta = 2\cos^2 \theta -1}\\&= \dfrac{1}{2} \int 1 + \cos 2\theta \phantom{x}d\theta\end{aligned}
We can then apply previous antiderivative techniques to integrate the resulting expression.
- Apply the sum rule for integrals and distribute the integral sign to each component.
- Use the constant rule, $\int a \phantom{x}dx = ax + C$, for the first integral.
- Apply u-substitution and use the antiderivative of $\cos$, $\int \cos x \phantom{x}dx = \sin x +C$, for the second group of integrals.
\begin{aligned}\dfrac{1}{2} \int 1 + \cos 2\theta \phantom{x}d\theta &= \dfrac{1}{2} \left[\color{Purple}\int 1\phantom{x}d\theta + \int\cos 2\theta \phantom{x}d\theta \right ],\phantom{x}\color{Purple} \text{Sum Rule}\\&= \dfrac{1}{2}\left[{\color{Purple}(\theta)+C} + \int\cos 2\theta \phantom{x}d\theta\right], \phantom{x}\color{Purple} \text{Constant Rule}\\&= \dfrac{1}{2}\left[\theta +{\color{Purple}\dfrac{1}{2}\left(\dfrac{\sin 2\theta}{2} +C \right )}\right], \phantom{x}\color{Purple} \text{u-Substitution & Antiderivative of Cosine}\\&= \dfrac{\theta}{2} + \dfrac{\sin 2\theta}{4} + C\end{aligned}
Now that we have integrated the expression in terms of $\theta$, let’s rewrite the result in terms of $\theta$ using the fact that $\theta = \sin^{-1} \left(\dfrac{x}{a}\right)$ , where $a =1$.
\begin{aligned}\int \cos^2 \theta\phantom{x}d\theta &=\dfrac{\theta}{2} + \dfrac{\sin 2\theta}{4} + C &= \dfrac{\sin^{-1}x}{2} + \dfrac{\sin 2\theta}{4} + C\end{aligned}
This will be the best time to construct a reference angle to rewrite this expression into simpler forms.
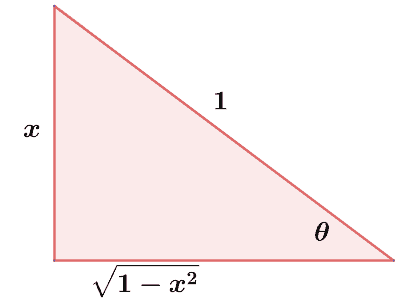
From this, we can see that $\sin \theta = \dfrac{x}{1}$ and $\cos \theta = \dfrac{\sqrt{1 – x^2}}{1}$. We can use the double-angle formula for sine, $\sin 2\theta = 2\cos\theta \sin \theta$, to rewrite the second term of the integral as shown below.
\begin{aligned}\sin \theta &= x\\\cos \theta &= \sqrt{1 – x^2}\\\sin 2\theta &= 2\sin \theta \cos \theta\\&= 2(x)(\sqrt{1 – x^2}) \\\\\dfrac{\sin^{-1}x}{2} + \dfrac{\sin 2\theta}{4} + C &= \dfrac{\sin^{-1}x}{2} + \dfrac{2x\sqrt{1 – x^2}}{4} + C\\&= \dfrac{\sin^{-1} x}{2} + \dfrac{x\sqrt{1 – x^2}}{2} + C\end{aligned}
This shows that through trigonometric substitution, we were able to find $\int \sqrt{1 -x^2}\phantom{x} dx$. In fact, we have $\int \sqrt{1 -x^2}\phantom{x} dx = \dfrac{\sin^{-1} x}{2} + \dfrac{x\sqrt{1 – x^2}}{2} + C $.
We can apply a similar approach to integrate expressions with the second and third forms, but we’ll leave save that for our next section! Make sure to review all sections first and take note of the guide tables and reference triangles before diving right into the problems below.
Example 1
Evaluate $\int \dfrac{1}{\sqrt{16 + x^2}}\phantom{x}dx$.
Solution
We can see that we have $\sqrt{16+ x^2}$ in the denominator, so we’ll be working with the general form, $\sqrt{a^2 + x^2}$. The best way to evaluate this integral is by substituting $x = a\tan \theta$ and $dx=a\sec^2 \theta\phantom{x} d\theta$ into the expression. Since we have $a^2=16$, we can use $a = 4$ for our trigonometric substitution.
\begin{aligned}x &= 4\tan \theta\\x^2 &= 16\tan^2 \theta\\dx &= 4\sec^2 \theta \phantom{x}d\theta\\\\\int \dfrac{1}{\sqrt{16+ {\color{Purple}x^2 }}}\phantom{x}{\color{Orange}dx} &= \int \dfrac{1}{\sqrt{16 + {\color{Purple}16\tan^2 \theta}}}{\color{Orange}\phantom{x}4\sec^2 \theta \phantom{x}d\theta}\\&= \int \dfrac{1}{\sqrt{16(1 + \tan^2 \theta)}} \phantom{x}4\sec^2 \theta \phantom{x}d\theta\end{aligned}
We can then use the Pythagorean identity, $\tan^2 \theta+ 1 = \sec^2 \theta$, to rewrite our expression inside the parenthesis. Cancel out common factors after to further simplify our integral.
\begin{aligned}\int \dfrac{1}{\sqrt{16+ x^2}}\phantom{x} dx&= \int \dfrac{1}{\sqrt{16(1 + \tan^2 \theta)}} \phantom{x}4\sec^2 \theta \phantom{x}d\theta \\&= \dfrac{1}{4\sqrt{\color{Purple}\sec^2 \theta}}\phantom{x}4\sec^2 \theta \phantom{x}d\theta,\phantom{x} \color{Purple}1 + \tan^2 \theta = \sec^2 \theta\\&=\int \sec \theta\phantom{x}d\theta\end{aligned}
Recall that we have learned about the antiderivative for $\sec \theta$ in the past, so we can use $\int \sec \theta \phantom{x}d\theta = \ln|\sec x + \tan x| + C$.
\begin{aligned}\int \dfrac{1}{\sqrt{16 + x^2}}\phantom{x} dx&=\int \sec \theta\phantom{x}d\theta\\&= \ln|\sec \theta + \tan \theta| + C\end{aligned}
We can use the fact that $\tan \theta = \dfrac{x}{4}$ and construct a reference triangle to help us rewrite the evaluated integral’s expression in terms of $x$.
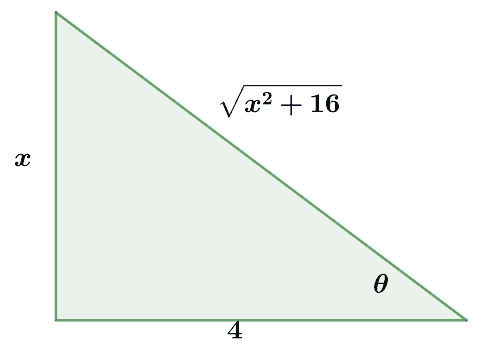
Using this reference triangle, we can express $\sec \theta$ and $\tan \theta$ in terms of $x$.
\begin{aligned} \sec \theta &= \dfrac{\sqrt{x^2 +16}}{4}\\\tan \theta &= \dfrac{x}{4}\end{aligned}
Let’s use these expressions to rewrite our evaluated integral’s expression.
\begin{aligned}\int \dfrac{1}{\sqrt{16 + x^2}}\phantom{x} dx&=\ln|\sec \theta + \tan \theta| + C\\&= \ln \left|\dfrac{\sqrt{x^2 + 16}}{4}+\dfrac{x}{4}\right|+C\\&=\ln \left|\dfrac{\sqrt{x^2 + 16} + x}{4}\right|+C\end{aligned}
Through trigonometric substitution (and thanks to our knowledge of trigonometric identities), we were able to evaluate $\int \dfrac{1}{\sqrt{16 + x^2}}\phantom{x}dx$. Hence, we have $\int \dfrac{1}{\sqrt{16 + x^2}}\phantom{x}dx =\ln \left|\dfrac{\sqrt{x^2 + 16} + x}{4}\right| + C $.
Example 2
Evaluate $\int \dfrac{\sqrt{x^2 -25}}{x^2}\phantom{x}dx$.
Solution
We can see that the integral we want to evaluate has $\sqrt{x^2 – 25}$, so this belongs to the third form ($\sqrt{x^2 +a^2}$) that meets the conditions for the trigonometric substitution method. In fact, for this case, we can let $x$ be $a\sec \theta$, where $a = 5$.
\begin{aligned}x&= 5\sec \theta\\x^2 &= 25 \sec^2 \theta\\dx&= 5\sec \theta \tan \theta \phantom{x}d\theta\\\\\int\dfrac{\sqrt{{\color{Purple}x^2} -25}}{x^2}\phantom{x}{\color{Orange}dx} &= \int\dfrac{\sqrt{{\color{Purple}25 \sec^2 \theta} -25}}{x^2}\phantom{x}{\color{Orange}5\sec \theta \tan \theta \phantom{x}d\theta}\\&= \int \dfrac{\sqrt{25(\sec^2 \theta-1)}}{25\sec^2 \theta} \cdot 5\sec \theta \tan \theta\phantom{x}d\theta\end{aligned}
We can rewrite the integral using the Pythagorean identity, $\tan^2 \theta = \sec^2 \theta – 1$.
\begin{aligned}\dfrac{\sqrt{x^2-25}}{x^2}\phantom{x}dx&=\int \dfrac{\sqrt{25({\sec^2 \theta-1)}}}{25\sec^2 \theta} \cdot 5\sec \theta \tan \theta\phantom{x}d\theta \\&= \int \dfrac{\sqrt{25({\color{Purple}\tan^2 \theta)}}}{25\sec^2 \theta} \cdot 5\sec \theta \tan \theta\phantom{x}d\theta,\phantom{x}\color{Purple} \tan^2 \theta=\sec^2 \theta – 1\\&= \int \dfrac{25\tan^2 \theta} {25\sec \theta}\phantom{x}d\theta\\&=\int \dfrac{\tan^2 \theta} {\sec \theta}\phantom{x}d\theta\\&= \int \dfrac{\sec^2 \theta-1}{\sec \theta}\phantom{x}d\theta\end{aligned}
We can further rewrite this expression so we can evaluate the integral in terms of $\theta$ as shown below.
- Separate the rational fraction as the difference between two simpler fractions.
- Take the integral of $\sec \theta$ using the antiderivative rule, $\int \sec x\phantom{x}dx = \ln|\sec x + \tan x| + C$.
- For the second term, we can rewrite $\dfrac{1}{\sec x}$ as $\cos x$ and use the antiderivative rule, $\int \cos x \phantom{x}dx = -\sin x$.
\begin{aligned}\int \dfrac{\sqrt{x^2-25}}{x^2}\phantom{x}dx&=\int \dfrac{\sec^2 \theta}{\sec \theta}\phantom{x}d\theta-\int \dfrac{1}{\sec \theta}\phantom{x}d\theta\\ &=\int\sec \theta\phantom{x}d\theta-\int \dfrac{1}{\sec \theta}\phantom{x}d\theta\\ &=\int\sec \theta\phantom{x}d\theta-\int \cos \theta\phantom{x}d\theta\\&= \ln|\sec \theta + \tan \theta| -(-\sin \theta) + C\\&= \ln|\sec \theta + \tan \theta| +\sin \theta + C\end{aligned}
We’ve now evaluated the integral in terms of $\theta$, so it’s time we construct a reference triangle to guide is in rewriting the expression in terms of $x$ this time.
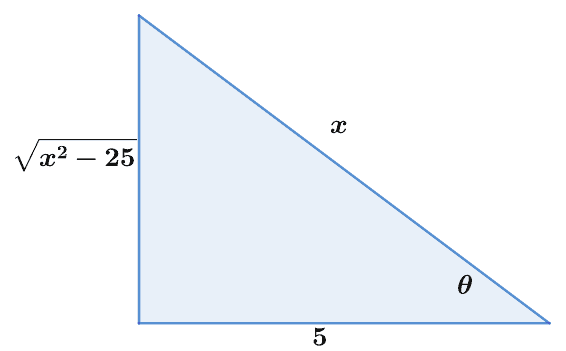
Using this reference triangle and the fact that $\sec \theta=\dfrac{x}{5}$, we can write $\sin \theta$ and $\tan \theta$ in terms of $x$.
\begin{aligned}\sin \theta &= \dfrac{\sqrt{x^2-25}}{x}\\\tan \theta &= \dfrac{\sqrt{x^2 – 25}}{5}\end{aligned}
Hence, we have $\int \dfrac{\sqrt{x^2-25}}{x^2}\phantom{x}dx = \ln\left|\dfrac{\sqrt{x^2 – 25}+ x}{5} + \tan\theta\right| + \dfrac{\sqrt{x^2- 25}}{x}+C$.
Practice Questions
1. Evaluate the following integrals.
a. $\int \sqrt{4–x^2} \phantom{x}dx$
b. $\int \sqrt{25+x^2} \phantom{x}dx$
c. $\int \sqrt{x^2-16} \phantom{x}dx$
2. Evaluate the following integrals.
a. $\int \dfrac{1}{\sqrt{x^2+9}} \phantom{x}dx$
b. $\int \dfrac{x^2}{\sqrt{x^2–36}} \phantom{x}dx$
c. $\int -2x^2\sqrt{81–x^2} \phantom{x}dx$
Answer Key
1.
a. $2\sin^{-1}\left(\dfrac{x}{2}\right) + \dfrac{x\sqrt{4 – x^2}}{2}$
b. $\dfrac{x\sqrt{25 + x^2}}{2} + \dfrac{1}{2}\ln \left(\dfrac{1}{5} |x + \sqrt{25 + x^2}|\right) + C$
c. $\dfrac{x\sqrt{x^2 – 16}}{2}+\dfrac{1}{2}\ln \left(\dfrac{1}{4} |x+\sqrt{x^2 – 16}|\right) + C$
2.
a. $\ln\left|\dfrac{\sqrt{x+9 +\sqrt{x^2 + 9}}}{3}\right|+C$
b. $\dfrac{x\sqrt{x^2 -36}}{2}+18\ln\left|\dfrac{\sqrt{x^2-36}+x}{6}\right|+C$
c. $\dfrac{x(1 -2x^2)\sqrt{1–x^2}}{4}-\dfrac{\sin^{-1}x}{4}+C$
Images/mathematical drawings are created with GeoGebra.