Unit Circle – Explanation and Examples

The unit circle is a circle in the Cartesian plane centered at the origin and with a radius of $1$.

This circle is useful for analyzing angles and trigonometric ratios. Typically, the initial angle is the line segment extending from the origin to the point $(1, 0)$. Then, the orientation in the plane helps determine positive and negative values for trig functions.

While the unit circle is fundamental to trigonometry, it is also important in all branches of science, mathematics, and engineering that use trigonometry.

Before we move on with the information of this section, make sure to review trigonometric ratios and angles.

What Is a Unit Circle?

A unit circle is a circle that has a radius of one unit and lies in the Cartesian coordinate plane with a center at the origin, $(0, 0)$. The unit circle is incredibly important in trigonometry because it is easy to create angles using the radii of this circle.

These angles are easily denoted by the point at which their terminal angle intersects the circumference of the circle. Then, it is simple to create a right triangle using these radii. A vertical line segment connecting the intersection of the terminal radius and the circumference to the x-axis creates such a triangle. 

In this triangle, the hypotenuse is a radius of the circle, so it has a length of $1$. The sine and cosine then are just the lengths of the vertical segment and the horizontal segment, respectively. This physical representation makes calculations easy and allows the viewer to visualize angles that do not make sense when only considering the triangle itself, such as obtuse angles and reflex angles.

Equation of the Unit Circle

A unit circle has this equation:

$x^2+y^2 = 1$.

This looks very similar to the trigonometric identity:

$sin^2\theta+cos^2\theta = 1$.

And that is not an accident. If the $x$ coordinate and the $y$ coordinate of any point on the circumference are squared and added together, they equal one. The $x$ value is the horizontal distance from the origin and the $y$ value is the vertical distance from the origin. 

Now, consider constructing a right triangle with one point at the origin, one point on the circumference, and the third point on the x-axis. Then, sine is equal to the vertical distance of the point on the circumference and cosine is equal to the horizontal distance of the point on the circumference.

Unit Circle in Trigonometry

When analyzing angles in a unit circle, the initial angle is always the radius extending from the origin to the point $(1, 0)$. This is a horizontal line extending to the right of the center. 

The terminal ray will be another radius of the circle. Then, the coordinates $(x, y)$ of the point where this radius intersects the circumference will be the cosine and sine of the angle, respectively.

This gives a visualization for trigonometric ratios greater than a right angle and provides more context for the sign of trig function values. If the $x$ value of the intersection is negative, the cosine is negative. If the $y$ value of the intersection is negative, the sine is negative.

These two trig functions set the basis for the other four, which build off of sine and cosine.

• Cosecant is the reciprocal of sine.
• Secant is the reciprocal of cosine.
• Tangent is sine divided by cosine.
• Cotangent is the reciprocal of tangent or cosine divided by sine.

Examples

This section covers common examples of problems involving the unit circle and their step-by-step solutions.

Example 1

Let point A be the origin, let B be the point $(0, 1)$ on the circumference of the unit circle, and let C be the point $(\frac{1}{3}, \frac{2\sqrt{2}}{3})$.

What is the tangent of the angle $BAC$?

Solution

It might help to draw a picture of this situation.

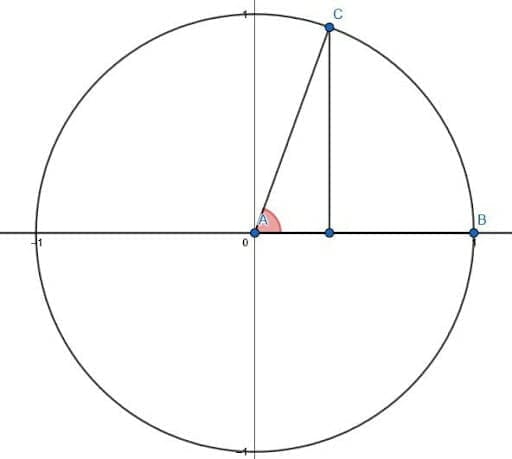
Here, the angle $BAC$ is the central angle, and AB and AC are both radii of the unit circle.

Now, the sine of the interior angle will be equal to the vertical distance from the horizontal axis to the point, C. Similarly, the cosine of the interior angle will be equal to the horizontal distance from the y axis to the point C.

But these distances are the $y$ coordinate and the $x$ coordinate of $C$, respectively. Therefore, the sine of the angle $BAC$ is $\frac{2\sqrt{2}}{3})$, and the cosine is $\frac{1}{3}$.

That is, knowing the measure of the angle is not necessary in order to determine the angle’s sine and cosine in the unit circle.

Example 2

Use the sign values of the $x$ and $y$ values along the circumference of the unit circle to determine the sign values of sine and cosine in the four different quadrants.

Solution

Recall that the quadrants in the Cartesian plane are separated by the x and y axes. The first quadrant is the one to the upper right, the second is to the upper left, the third to the lower left, and the fourth to the lower right.

That is, points in the first quadrant have both positive $x$ and $y$ values. In the second quadrant, points have a negative $x$ value and a positive $y$ value. In the third, both are negative, and in the fourth, only the $y$ values are negative.

Since the unit circle has its center at the origin, it has points in all four quadrants. Any angles formed with radii that intersect the circle in the first quadrant will have positive sine and cosine because the intersection has positive coordinates.

On the other hand, any angles formed by radii that intersect the circle in the second quadrant will have negative cosine and positive sine. This is because x-values are negative in the second quadrant.

Similarly, since both coordinates are negative in the third quadrant, angles whose terminal ray intersects the unit circle in this quadrant have negative sine and cosine. Finally, in the fourth quadrant, x values and cosine are positive, but y values and sine are negative.

Since the first quadrant includes angles between $0$ and $90$ degrees or $0$ and $\frac{\pi}{2}$ radians, this means sine and cosine are both positive in this range. 

Similarly, the second quadrant includes angles from $90$ degrees to $180$ degrees or $\frac{\pi}{2}$ to $\pi$ radians. This means that sine is negative and cosine is positive for angles in this range.

The third quadrant includes angles between $180$ and $270$ degrees or $\pi$ and $\frac{3\pi}{2}$ radians. These will consequently have negative sine and cosine values.

Finally, the angles in the fourth quadrant range from $270$ to $360$ degrees or $\frac{3\pi}{2}$ and $2\pi$ radians. Their sine values will be negative, but their cosine values will be positive.

Example 3

An angle has a sine value of $\frac{2}{2\sqrt3}$. What is its corresponding cosine value?

Solution

This problem requires using the identity $sin^2x+cos^2x = 1$.

In this case, $sin^2x = (\frac{2}{3\sqrt{3}})^2 = \frac{4}{27}$.

Then, cosine squared is equal to $1-\frac{4}{27} = \frac{23}{27}$.

Therefore, cosine is equal to $\sqrt{\frac{23}{27}}$.

Example 4

Find the tangent of an angle whose terminal ray intersects the unit circle at the point $(\frac{3}{4}, \frac{\sqrt{7}}{4})$.

Solution

The tangent of an angle is equal to its sine divided by its cosine. Then, recall that the cosine of any angle is equal to the x-value of the terminal ray’s intersection with the unit circle. Similarly, the sine is equal to the y-value of the terminal ray’s intersection with the unit circle. 

Therefore, in this case, the tangent is equal to the $y$ value divided by the $x$ value. Note that this is equal to the slope of the radius which has a point at the origin and this point, $(x, y)$.

Example 5

What is the relationship between the sine and cosine of an angle $\theta_1$ and an angle coterminal to it, $\theta_2$?

Solution

Since coterminal angles have the same terminal ray by definition, the terminal ray of each angle will intersect the unit circle at the same point. This intersection’s x-value is the cosine of the angle, and the y-value is the sine of the angle. 

Therefore, coterminal angles will have the same sine and cosine ratios.