Vector Components – Explanation and Examples

In vector geometry, vector components are one of the most significant and vital concepts. The entire foundation of vector geometry is established on vector components. 

Vector components are defined as:

“Splitting of an angled vector into two vectors directed towards the coordinate axes in a two-dimensional coordinate system are defined as vector components.”

We will be covering the following concepts in Vector Components:

• What are the components of a vector?
• How to find the components of a vector?
• What is the formula for vector components?
• Examples
• Practice questions 

What Are The Components Of A Vector?

The splitting of a vector into its 2 respective components directed along the respective axes is called vector components. This process is called the ‘resolution of a vector or vector in a plane.’ 

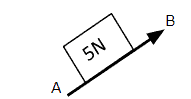
Suppose a vector AB exists in a two-dimensional coordinate system with x and y-axes. If this vector is not perfectly aligned with the coordinate axes, then the vector AB must be at some angle from the coordinate axes. 

For finding the direction and magnitude of such a vector that is angled in a two-dimensional plane, the vector AB is split into 2 corresponding components. The resulting two components are aligned with the x and y-axes. 

The two components into which the vector (let’s say AB) are resolved are directed in the horizontal and vertical directions. After the division of vector AB into its components, it can be concluded that the vector AB is the resultant of its 2 components, each directed along an axis. 

This theory can be proved by applying the head-to-tail rule. Consider a vector AB in a two-dimensional space. We can analyze that the two components are AC and BC as shown in the figure below:

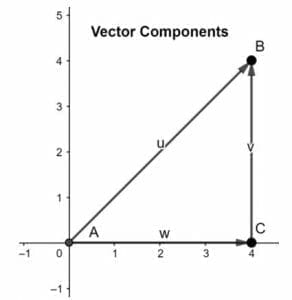
By applying the head-to-tail rule, we can observe that the tail of AC coincides with the tail of vector AB, and the head of vector component BC coincides with the head of vector AB, thus concluding vector AB as the resultant of its two vector components. 

Mathematically, it can be expressed as:

AB = AC + BC

Or

|AB| = |AC| + |BC| 

Let’s consider a practical example.

Suppose a plane is flying from Poland to Germany in the south-west direction. The vector representing this plane can be divided into two vector components; one directed towards the south, and the other directed towards the west. Hence, the angled vector directed south-west is the resultant of its two vector components. 

One thing to note is that a vector’s components are not actual vectors that exist in the two-dimensional space. They are only virtually present for the sole purpose of simplifying the vector analysis.  

The resolution of a vector into its corresponding vector components simplifies the calculations of vector geometry and can be implemented on real-life problems. 

When we consider the vector to be in a two-dimensional plane, it can only be resolved into two components, i.e., X and Y, but when a vector is three-dimensional, it has three components named X, Y, and Z corresponding to x, y, and z-axis. 

How To Find The Components Of A Vector?

The two components of any vector can be found through the method of vector resolution. Consider the vector as shown below, which exists in a two-dimensional plane. 

This vector AB is at an angle 𝛳 from the x-axis. To find the components of the vector AB, follow the below procedure:

1. Drop a perpendicular from the x-axis such that it coincides with the head of vector AB. 
2. Label it as BC. 
3. Similarly, draw a parallel line from the tail of the vector AB such that its head coincides with the tail of the vector component BC. 
4. Label it as AC.
5. The lines BC and AC will be the vector components of the vector AB.  

These two components are supposed to form a right-angled triangle. These components are then used to find the resultant vector’s magnitude and direction, which is AB.

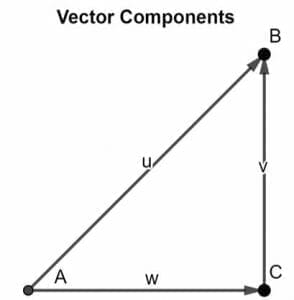
Consider a vector v. Its two components directed along the x and y-axis would be vx and vy, respectively. To find the magnitude and direction of the vector v, we would need to find the magnitude and direction of its vector components first. 

For this, we follow the vector component formula.

What Is The Vector Component Formula?

The formula for finding a vector’s components is quite simple and is widely used to solve problems in Mathematics and Physics. 

As we mentioned earlier, the two vector components of a vector v are vx and vy. To completely solve the vector v in terms of magnitude and direction, we would need to calculate these components first. 

Finding Magnitude Of The Vector Components

Following are the formulas for the calculation of the magnitudes of the two vector components:

For vx :

vx = v.cosθ

For vy:

vy = v.sinθ

By following these formulas, we would get the magnitude of the two vector components. 

Example 1

Calculate and resolve the force vector into its component where the Force is of 10N and inclined at an angle of 30º in the given plane as shown below:

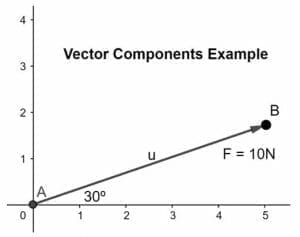
Solution

Given that the magnitude of the force is 10N where θ is given as 30º

Resolve the vector into its components, x-component along the x-axis and y-component along the y-axis such that the head of the x-component coincides with the tail of the second component according to the head-to-tail rule as shown in the figure below:

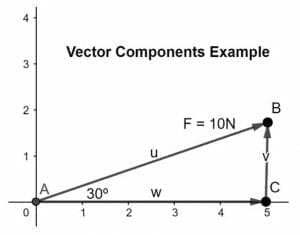
To find out the magnitude of the components, we will use the formulas stated below:

FX = F.cosθ   eq (1)

Fy = F.sinθ      eq (2)

where, F = 10N, θ = 30º

putting values in eq (1) and eq (2),  

FX = 1.545N

Fy = -9.881N 

So, the given vector is resolved into its x and y components

Finding Magnitude Of The Vector Through Components

Now that we have calculated the magnitude of the vector components, the next step is to calculate the magnitude of the vector v. 

Basically, the magnitude of vector v is the distance between the initial and final points. The symbol for the magnitude of vector v is defined as |v|.

There are two ways to calculate the magnitude of a vector:

• Calculating the magnitude of the vector using the distance formula.
• Calculating the magnitude of a vector using the resolution of vector components.

Using The Distance Formula

If the coordinates of the two points, the initial and final, are given, then the distance formula can calculate the magnitude of the vector v.

Let the coordinates of initial point A be (x1 ,y1) and the final point B be (x2 ,y2). Then, the formula is defined as:

 |v| = √((x2 – x1)2 +(y2 -y1)2) 

Using Vector Components

Since the given vector v is resolved into its x and y components vx and vy, respectively.

The following formula is applied to calculate the magnitude of vector v:

|v| = √((vx )^2+( vy)^2)

Where vx=vcosθ and vy=vsinθ.

The magnitude of vector v is represented by |v|, and it will be the magnitude of the resultant of the two vector components. 

Note: The magnitude of a vector can be represented in two ways; either in italics v or in absolute form |v|. 

Example 2

Calculate the magnitude of vector v = (3,8).

Solution

As we know that, 

|v| = √((vx )^2+( vy)^2)

Where vx = 3 , vy =8

Putting into the formula give

|v| = √((3)^2+(8)^2)

|v| = 8.544

Example 3

A force of 12N is acting on a boat at an angle of 51o with the horizontal. Resolve into its components and prove by using the formula that the magnitude of the force is 12N.

Solution

As we know that,  

Fx= F.cosθ

Fx= 12.cos51

Fx= 8.91N

Fy = F.sinθ

Fy = 12.sin51

Fy = 8.04N

Now, prove using the magnitude formula that the magnitude of the force given in the question is 12N.

Using formula,

|F| = √ ((Fx )^2+( Fy)^2)

|F| = √ ((8.91 )^2+( 8.04)^2)

|F|=12.00N

Hence, it proved using the formula that the magnitude of the force is 12N

Finding Direction Of The Vector Through Components

The direction of the vector v is the measure of the angle that it makes with the horizontal in the plane

Following is the formula used to calculate the direction of the resultant vector.

θ = tan-1 (vy/vx)

θ = tan-1 (vsinθ/vcosθ)

This is the angle which resultant vector makes with the +x-direction in an anticlockwise manner. The signs of vx and vy will determine the quadrant in which it lies.

To determine θ, we will use the following conventions:

1. Irrespective of signs, find the value of tan-1 (vy/vx) and name this angle as φ.
2. If both vx and vy are positive φ = θ
3. If both are negative θ =180º + φ 
4. If vx is positive and vy is negative θ = 360º – φ 
5. If vx is negative and vy is positive θ = 180º – φ 

Example 4

Find the value of θ if vx =15 and vy =8.66.

Solution

As we know the formula. 

θ = tan-1 (vy/vx)

θ  = tan-1 (8.66/15)

 θ = 30º

Example 5

Find out the magnitude and direction of a vector OP= (-4,6).

Solution

The magnitude of the vector is defined as,

|OP| = √ ((-4)^2 +(6)^2)

|OP| = √ (16+36)

|OP| = 7.21

The direction of the given vector is,

  φ = tan-1 (6/4)

φ = 56.3º

Since the x-component is negative and the y-component is positive so, it lies in the second quadrant, and according to the convention explained above, θ is given as,

θ = 180º – φ

θ = 180º – 56.3º

 θ = 123.7º

Practice Problems:

1. A force of 20N inclined at an angle of 67º on the surface. Resolve the vector into its component and calculate the magnitude of the given force.
2. Resolve the vector shown in the figure below according to the head-to-tail rule and label them accordingly: 
3. Two forces, A = (4,5) N and B = (3,7) N acting at a point P. Calculate the magnitude of the resultant force.
4. Find out the magnitude and direction of the vectors given: u = (-7,6) and v= (5,9)
5. Find the magnitude and direction of the vector initial point P(-3,1) and end point Q(-2,-5).            

 Answers:

1. FX = -10.4N , FY = -17.1N, R = 20N
2. Refer to example 1 and draw accordingly.
3. R = 13.9N
4. |u| = 9.2 , θ = 150.250          |v| = 10.3 , θ = 60.90    
5. |PQ| = 6.08 , θ = 279.

All the vector diagrams are constructed by using GeoGebra. 

Previous Lesson | Main Page | Next Lesson