Vectors Equation of a Line – Definition, General Forms, and Examples

The vectors equation of a line shows us how we can model lines with direction and in three-dimensional space. Through vectors, we’ll have another way to uniquely define a straight line. Vector equations are important in aeronautical engineering, physics, astronomy, and more, so it is essential that we establish our foundations of vectors equation – starting from the most basic surfaces.

The vector equation of a line can be established using the position vector of a particular point, a scalar parameter, and a vector showing the direction of the line. Through vector equations, we can now establish equations of a line in three-dimensional space.

In this article, we’ll show you how we establish the definition of the vector equation of the line using what we know of vectors and lines in the two-dimensional coordinate system. We’ll also see how we can translate the test for parallel and perpendicular lines in a 3D coordinate system. For now, let’s begin by establishing the fundamental components of vector equations of a line!

What is the vector equation of a line?

The vector equation of a line conceptually represents the set of all points that satisfy the following conditions:

• These points contain a specific point we can initially work with which we establish as the position vector: $\textbf{r}_o$.
• The vector formed between $\textbf{r}_o$ and the position vector, $\textbf{r}$,on the line is parallel to a vector, $\textbf{v}$.

The line’s vector equation is represented by its general form shown below.

\begin{aligned} \textbf{r} = \textbf{r}_o + t\textbf{v},\end{aligned}

where $\textbf{r}_o$ represents the initial position of the line, $\textbf{v}$ is the vector indicating the direction of the line, and $t$ is the parameter defining $\textbf{v}$’s direction.

We’ll better understand the line’s vector equation by reviewing what we know of lines in $xy$-plane and translate that to define lines in 3D space. In an $xy$-plane, the line is determined when we’re given an initial point and slope. In fact, we’ve learned that we can express the line’s equation as either of the two forms.

\begin{aligned}y &= mx + b\\ &: m = \text{slope}, b = \text{intercept}\\y – y_o &= m(x – x_o)\\ &: (x_o, y_o) = \text{initial point}, m = \text{slope}\end{aligned}

Using the same thought process, we can also write the equation of the line in $\mathbb{R}^3$ when we’re given an initial point, $P(x_o, y_o, z_o)$, that lies on the line, $L$, and have the line’s direction. In three dimensions, we can describe the line’s direction using the vector, $\textbf{v}$. Make sure that $\textbf{v}$ is parallel to our line, $L$.

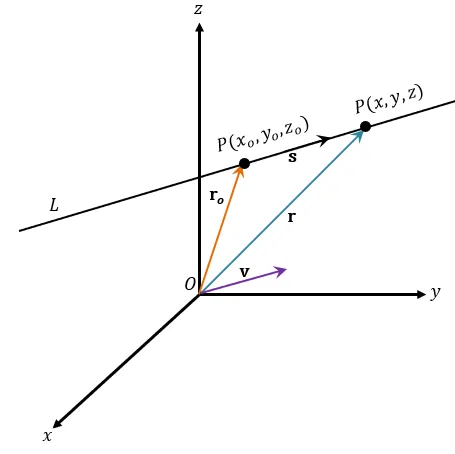
Let’s say we have an arbitrary point, $P(x, y, z)$, on the line $L$. We also establish that $\textbf{r}_o$ and $\textbf{r}$ are position vectors of both points – $P_o$ and $P$. Suppose that $\textbf{s}$ is represents the vector formed by $P_o$ and $P$: $\overrightarrow{P_oP}$ then through vector addition, we’ll have $\textbf{r} = \textbf{r}_o + \textbf{s}$. The vectors $\textbf{s}$ and $\textbf{v}$ are parallel, so we can define $\textbf{s}$ as product of  a scalar factor and the vector, $\textbf{v}$: $\textbf{s} = t\textbf{v}$. Hence, we established the equation for the line in 3D coordinate system.

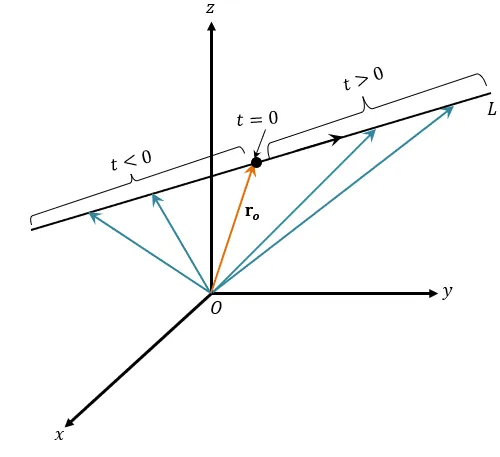
Let’s now take a look at the parameter, $t$, and consider its signs along the line, $L$. The graph above highlights what happens when $t <0$ and $t > 0$. Why don’t we write our vector expressions in their component forms?

Use these component forms to rewrite the vector equation of $L$ shown below.

\begin{aligned} \textbf{r} &= \textbf{r}_o + t\textbf{v}\\<x, y, z> &= <x_o, y_o, z_o> + \\&= \end{aligned}

As we know, vectors will only be equal when these two expressions are equal. This means that we can break down our previous vector equation into three scalar equations and we call these equations the parametric equations.

We’ve now established the general forms of the vector and parametric equations of the line in three-dimensional space.

What are other equations essential for the line in 3D space?

We’ll now discuss other properties and vector equations of the line, $L$. When working with the vector, $\textbf{v} = <a, b , c>$, that describes the line, $L%%EDITORCONTENT%%gt;, we call $a$, $b$. and $c$ the direction numbers of the line, $L$.

The line, $L$, can also be defined without the parameter, $t$. First, isolate $t$ from the left-hand side of each of the parametric equations.

\begin{aligned}t &= \dfrac{x- x_o}{a}\\ t &= \dfrac{y- y_o}{b}\\ t &= \dfrac{z- z_o}{c}\end{aligned}

We call this set of equations the symmetric equations.

We’ll now discuss other properties and vector equations of the line, $L$. When working with the vector, $\textbf{v} = <a, b , c>$, that describes the line, $L%%EDITORCONTENT%%gt;, we call $a$, $b$. and $c$ the direction numbers of the line, $L$.

We’ll now consider expressing the equation of the line segment formed between two points, $\textbf{r}_o$ and $\textbf{r}_1$. If the line, $\textbf{r}_o$, asses through the end of $\textbf{r}_1$, we can express $\textbf{v}$ as $\textbf{r}_1 – \textbf{r}_o$.

\begin{aligned}\textbf{r} &= \textbf{r}_o + t\textbf{v} \\&= \textbf{r}_o + t(\textbf{r}_1 – \textbf{r}_o) \\&= (1 – t) \textbf{r}_o + t\textbf{r}_1 \end{aligned}  

When given two lines, $L_1$ and $L_2$, in $\mathbb{R}^3$, they can either intersect each other, are parallel to each or are skew lines.

• The two lines intersect each other at a point, $P$, then there exists a component, ($x$, $y$, and $z$) such that a set of parameter values for each line will satisfy all three equations.
• The two lines are parallel if and only if their vector components share a common scalar factor.
• The two lines are skew when the lines neither intersect each other nor are they parallel to each other.

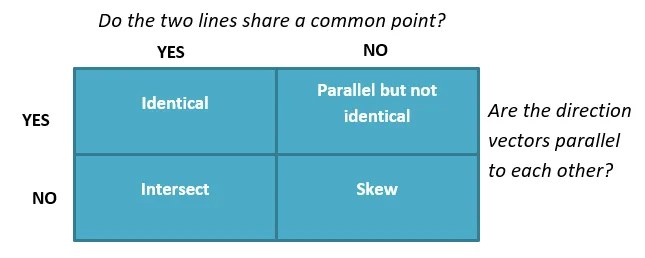
Here’s a guide summarizing the relationships that two lines may share. We’ve covered all the fundamentals of the vector equation. Now, let’s explore how we can use what  we’ve learned to define a given line’s equation in 3D space.

How to find the vector equation of a line?

Finding the vector equation of a line is straightforward – take note of the given vectors and point and apply the general form for vector equations: $\textbf{r} = \textbf{r}_o + t\textbf{v}$.

• Find the vector representing $\textbf{r}_o$.
• Find the expression of the vector that is parallel to our line, $\textbf{v}$.
• Use these two expressions to define the line’s vector equation.

This means that we can now find the vector equation of the line defined by the point, $(2, 4, 3)$, and is parallel to the vector, $2\textbf{i} -3\textbf{j} + \textbf{k}$, by finding the expressions for $\textbf{r}_o$ and $\textbf{v}$ as shown below.

\begin{aligned}r_o &= (2, 4, 3) \\\textbf{r}_o &= 2\textbf{i} + 4\textbf{j} + 3\textbf{k}\\\textbf{v} &= 2\textbf{i} -3\textbf{j} + \textbf{k}\\\\\textbf{r} &= \textbf{r}_o + t\textbf{v}\\&= (2\textbf{i} + 4\textbf{j} + 3\textbf{k}) +  t(2\textbf{i} -3\textbf{j} + \textbf{k})\\&=(2 + 2t)\textbf{i} + (4 -3t)\textbf{j} + (3 + t)\textbf{k}\end{aligned}

This means that we can now find the vector equation of the line defined by the point, $(2, 4, 3)$, and is parallel to the vector, $2\textbf{i} -3\textbf{j} + \textbf{k}$, as shown below.

We can also apply a similar process to find the parametric equations of the line. This time, we’ll use the general form:

\begin{aligned}x&= x_o + at \\ y&= y_o + bt\\ z&= z_o + ct \end{aligned}

Using our previous example, $\textbf{r}_o = <2, 4, 3>$, and is parallel to the vector, $\textbf{v} = 2 \textbf{i} -3\textbf{j} + \textbf{k}$. Hence, we have the following:

We’ve prepared more examples for you to master this topic. When you’re ready, head over to the next section!

Example 1

Find the equation of the line passing through $(2, 5, -4)$ and is parallel to the vector, $\textbf{v} = 6\textbf{i} + 5\textbf{j} – 2\textbf{k}$. Write its vector and parametric equations.

Solution

First, we’ll define $\textbf{r}_o$ as $2\textbf{i} + 5\textbf{j} – 4\textbf{k}$. We want the line to be parallel to the vector, $\textbf{v} = 6\textbf{i} + 5\textbf{j} – 2\textbf{k}$. We’ll use these two vectors to find the vector equation of the line using.

\begin{aligned}\textbf{r}_o &= 2\textbf{i} + 5\textbf{j} – 4\textbf{k} \\\textbf{v} &= 6\textbf{i} + 5\textbf{j} – 2\textbf{k}\\\\\textbf{r} &= \textbf{r}_o + t\textbf{v}\\&= (2\textbf{i} + 5\textbf{j} – 4\textbf{k}) +  t(6\textbf{i} + 5\textbf{j} – 2\textbf{k})\\&= (2 + 6t)\textbf{i} + (5 + 5t)\textbf{j} + (-4 – 2t)\textbf{k}\end{aligned}

Now, let’s write both $\textbf{r}_o$ and $\textbf{v}$ in their component forms: $\textbf{r}_o = <2, 5, -4>$ and $\textbf{v} = <6, 5, -2>$. We’ll use these values to write down the parametric equations representing the line.

 This means that the line has the following equations:

• A vector equation of $(2 + 6t)\textbf{i} + (5 + 5t)\textbf{j} + (-4 – 2t)\textbf{k}$.
• Parametric equations of $x = 2 + 6t$, $y = 5 + 5t$, and $z = -4 – 2t$.

Example 2

Find the equation of the line passing through the two points, $(2, -4, 3)$ and $(1, -2, 5)$. Write down the equation of the line in three forms: its vector, parametric, and symmetric equations.

Solution

We’re now given two points, so we’ll need to find the expression for the vector, $\textbf{v}$. If the line passes through the two points, there is a vector parallel to the line that has $(2, -4, 3)$ and $(1, -2, 5)$ as their endpoints. Simply subtract the two points to find the components of $\textbf{v}$.

\begin{aligned}\textbf{v} &= <(2 – 1), (-4 – -2), (3 – 5)>\\&= <-1, -2, -2>\end{aligned}

Keep in mind that you can also reverse the order and subtract the first point from the second point. Now that we have the vector components, we’ll use either of the two points to write the vector equation of the line:

\begin{aligned}\textbf{r}_o &= <2, -4, 3>\\ \textbf{v} &= <-1, -2, -2>\\\\\textbf{r} &= \textbf{r}_o + t\textbf{v}\\&= <2, -4, 3> + t<-1, -2, 2>\\&= <2 – t, -4 -2t, 4 + 2t> \\&= (2 – t)\textbf{i} + (-4 – 2t)\textbf{j} + (4 + 2t) \textbf{k}\end{aligned}

Since we’re working with the same vectors, we’ll use the same vector components to find the parametric equations representing the line.

Noticed something? The vector components of the vector equation actually show us the parametric equations of the line. Knowing this will definitely save you time when working on vector and parametric equations.
Use the components from our parametric equations to set up the symmetric equations of the line. We can do this by rewriting each parametric equation in the following forms:

\begin{aligned}\dfrac{x – x_o}{a} = \dfrac{y – y_o}{b} = \dfrac{z – z_o}{c}\end{aligned}

Hence, the symmetric equation representing the line is $\dfrac{x – 2}{-1} = \dfrac{y +4}{-2} = \dfrac{z – 4}{2}$.

Example 3

Show that the lines with the following parametric equations are parallel.

\begin{aligned}x = 2 + 6t_1,  &y = -1 + 4t_1, z = 7 – 2t_1\\ x = -4 + 3t_2, &y = 6 + 2t_2, z = 10 – t_2\end{aligned}

Solution

Two lines are parallel when their corresponding vectors’ direction numbers share a common factor. Recall that direction numbers correspond to the coefficients before the parameters, $t_1$ and $t_2$. Hence, we have the following direction numbers for the two:

• Direction numbers of $x$ : $6, 4, -2$
• Direction numbers of $y$ : $3, 2, -1$

From this, we can see that the direction numbers of the first parametric equations are twice that of the second set of parametric equations. This means that the lines are parallel and confirm the statement.

Practice Questions

1. Find the equation of the line passing through $(3, -1, -2)$ and is parallel to the vector, $\textbf{v} = 2\textbf{i} + 4\textbf{j} +6\textbf{k}$. Write its vector and parametric equations.

2. Find the equation of the line passing through the two points, $(5, 2, -4)$ and $(3, 1, -3)$. Write down the equation of the line in three forms: its vector, parametric, and symmetric equations.

3. What is the set of parametric equations that represent the line segment formed by the two points: $(2, 1, 4)$ and $(3, -1, 3)$?

4. Show that the lines with the following parametric equations are parallel.
\begin{aligned}x = 8 + 8t_1, &y = -3 + 12t_1, z = 5 – 4t_1\\ x = 6 + 2t_2, &y = 6 + 3t_2, z = 8 – t_2\end{aligned}

Answer Key

1.
Vector equation: $(3 + 2t)\textbf{i} + (-1 + 4t)\textbf{j} + (-2 + 6t)\textbf{k}$.
Parametric equations: $x = 3 + 2t$, $y = -1 + 4t$, and $z = -2 + 6t$.
2.
Vector equation: $(5 – 2t)\textbf{i} + (2 – t)\textbf{j} + (-4 – t)\textbf{k}$.
Parametric equations: $x = 5 – 2t$, $y = 2 – t$, and $z = -4 – t$.
Symmetric equation: $\dfrac{x – 5}{-2} = \dfrac{y – 2}{-1} = \dfrac{z + 4}{-1}$.
3. $x = 2 + t, y = 1 – 2t, z = 4 – t$, where $0 \leq t \leq 1$
4. The first set of parametric equations has directions numbers that are four times larger than the second set of parametric equations. Hence, the lines are parallel.