- Home
- >
- Vertical asymptotes – Properties, Graphs, and Examples
JUMP TO TOPIC
Vertical asymptotes – Properties, Graphs, and Examples
 Ever noticed the vertical dashed lines included in some of the graphs in your class? These special lines are called vertical asymptotes, and they help us understand the input values that a function may never cross on a graph.
Ever noticed the vertical dashed lines included in some of the graphs in your class? These special lines are called vertical asymptotes, and they help us understand the input values that a function may never cross on a graph.
Vertical asymptotes represent the values of $\boldsymbol{x}$ that are restricted on a given function, $\boldsymbol{f(x)}$. These are normally represented by dashed vertical lines.
Learning about vertical asymptotes can also help us understand the restrictions of a function and how they affect the function’s graph. This article will show everything we need to know what vertical asymptotes represent, learn how to graph them, and interpret graphs from their asymptotes.
What is a vertical asymptote?
A rational function’s vertical asymptote will depend on the expression found at its denominator. Vertical asymptotes represent the values of $x$ where the denominator is zero.
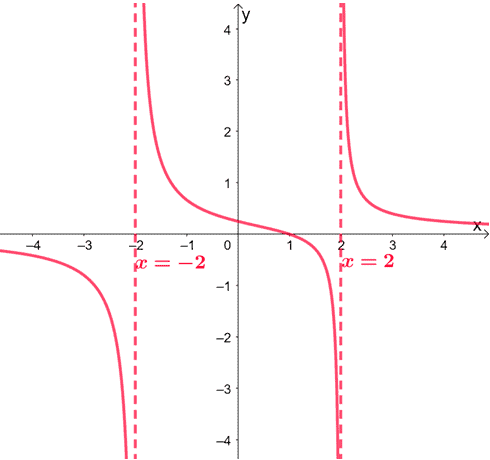
Here’s an example of a graph that contains vertical asymptotes: $x = -2$ and $x = 2$. This means that the function has restricted values at $-2$ and $2$. Notice how the graph’s curve never passes through the vertical asymptotes? This applies to all functions containing vertical asymptotes.
We can also interpret the vertical asymptotes as the value of $a$ where $\lim_{x \rightarrow a} f(x) = \infty$.
How to find the vertical asymptote?
Vertical asymptotes are not limited to the graphs of rational functions. Logarithmic and some trigonometric functions do have vertical asymptotes. In general, we can determine the vertical asymptotes by finding the restricted input values for the function.
If given the graph, we can identify the vertical asymptote by finding the value or values of $x$, where $f(x)$’s curve tries to approach but never reaches.
Now, what if we’re given the equation or algebraic expression of a rational function? Here are some important reminders to keep in mind when determining its vertical asymptotes.
Vertical asymptote rules for rational functions
First, let’s recall that rational functions can be expressed as $f(x) = \dfrac{p(x)}{q(x)}$, where $p(x)$ and $q(x)$ are polynomial functions. We can find the values where $f(x)$ are not valid by equating the $q(x)$ to $0$.
Here are some important steps to follow when solving for vertical asymptotes:
- Start by factoring the numerator and the denominator of $f(x)$.
- Observe if the numerator ($p(x)$) and the denominator ($q(x)$) share common factors.
- Identify whether the factors in the denominator are considered discontinuities or vertical asymptotes.
Rule 1: If $\boldsymbol{x – a}$ is common factor shared by the numerator and denominator of $\boldsymbol{f(x)}$, consider $\boldsymbol{x = a}$ as a discontinuity or a hole.
Whenever we locate a shared factor between the numerator and the denominator, we can cancel this factor and take note of $a$.
Once we have the simplified form of $f(x)$, let’s find the value of $f(a)$ and take note of $(a, f(a))$ as a discontinuity.
Let’s go ahead and observe $f(x) = \dfrac{x^3 – 5x^2 + 6x}{x^2 – 9}$.
The first thing we should do is to express both the denominator and numerator of $f(x)$ in factored forms.
$\begin{aligned} \dfrac{x^3 – 5x^2 + 6x}{x^2 – 9} &= \dfrac{x(x^2 – 5x + 6)}{(x- 3)(x + 3)}\\ &= \dfrac{x(x -2)(x – 3)}{(x- 3)(x + 3)}\end{aligned}$
Since $(x -3)$ is a common factor shared by the numerator and denominator, we can consider $x = 3$ as a discontinuity. Cancel out $(x – 3)$ and substitute $x = 3$ back into the simplified expression of $f(x)$.
$\begin{aligned} f(x) &= \dfrac{x(x -2)\cancel{(x – 3)}}{\cancel{(x – 3)}(x + 3)}\\&=\dfrac{x(x- 2)}{x + 3}\\\\f(3)&=\dfrac{3(3 – 2)}{3 + 3}\\&=\dfrac{3}{6}\\&=\dfrac{1}{2}\end{aligned}$
This means that $f(x)$ actually has a hole at $\left(3, \dfrac{1}{2}\right)$. This coordinate will be represented by an unfilled dot on the $f(x)$’s graph.
If you want to learn more about holes found in rational functions, check out this article we wrote about discontinuities and holes.
Rule 2: If $\boldsymbol{x – a}$ is not common factor shared by the numerator and denominator of $\boldsymbol{f(x)}$, the equation $\boldsymbol{x = a}$ will now be a vertical asymptote.
If we can’t simplify a function any further by canceling common factors, the denominator’s remaining expression can now be equated to zero to find the restrictions on $x$.
Why don’t we apply this with the simplified form of $f(x)$ from our previous example?
We have $f(x) = \dfrac{x(x- 2)}{x + 3}$, so we can equate the denominator, $x + 3$, to zero.
$\begin{aligned} x + 3 &= 0\\ x&= -3\end{aligned}$
This means that $f(x)$ actually has a vertical asymptote at $x = -3$. This will be represented by a vertical dashed line on $f(x)$’s graph.
How to graph vertical asymptote?
After knowing a function’s vertical asymptote, why don’t we learn these vertical asymptotes are represented on an $xy$-coordinate system? Keep these important reminders in mind:
- The general form of vertical asymptotes is $x = a$, so the vertical asymptote will be a horizontal line (normally, it’s graphed as a dashed horizontal line).
- Graph a dashed vertical line that passes through $(a, 0)$ and extends both upwards and downwards.
- Keep in mind as well that the curve of a function will never pass through its vertical asymptote/s.
Let’s go ahead and graph the vertical asymptote of $f(x) = \dfrac{x^3 – 5x^2 + 6x}{x^2 – 9}$ at $x = -3$.
This means that its vertical asymptote will be a vertical dashed line that passes through the point $(-3, 0)$.

Let’s complete the graph by including the graph of $f(x)$ and its hole. Need a refresher on how to graph rational functions? Check out this article on rational functions and their graphs.
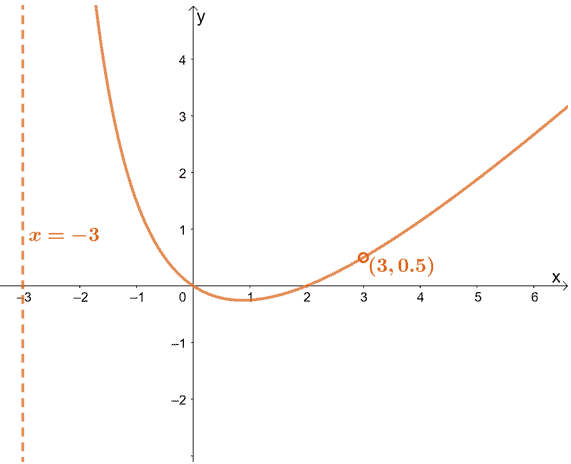
As you can see from the graph, $f(x)$’s graph never touches its vertical asymptote at $x = -3$. This also confirms what we know about vertical asymptotes: when $x \rightarrow –3$, $f(x) \rightarrow \infty$.
Summary of vertical asymptote definition and properties
We’ve already discussed everything we need to know about vertical asymptotes (and specifically, rational functions’ vertical asymptotes), so it’s time that we practice more examples.
Before we do, let’s go ahead and summarize everything we know so far.
- Vertical asymptotes represent the value of $a$ that will satisfy the equation $\lim_{x\rightarrow a} f(x) = \infty$.
- If the denominator and numerator of $f(x)$ shares a common factor, $(x – a)$, a we can find a hole at $(a, f(a))$.
- When $f(x)$ is in its simplified form, all values of $x$ that will make the denominator be zero are considered asymptotes of $f(x)$.
- Since its general form is $x = a$, vertical asymptotes are represented by vertical dashed lines.
- These lines should pass through the point $(a, 0)$.
Go back to these five-pointers when you need a refresher, and the rest will be fine. Let’s go ahead and practice what we’ve just learned!
Example 1
Fill in the blanks to make the following statements true.
a. If the denominator of $f(x)$’s simplified form is $x(x- 3)(x + 4)$, it has ________ vertical asymptotes.
b. If $f(x) = \dfrac{(x- 1)(x+ 2)(x – 3)}{(x +2)(x – 4)}$, $f(x)$ has a ____________ at $x = -2$ and a ____________________ at $x = 4$.
c. If $\lim_{x\rightarrow 4} f(x) = \infty$ and $\lim_{x\rightarrow -3} f(x) = \infty$, the function $f(x)$ has vertical asymptotes at ___________ and __________.
Solution
Always go back to the fact that vertical asymptotes are the values of $x$ where the rational function’s denominator is equal to $0$.
a. Since $f(x)$ is already simplified and has three unique factors in the denominator; it has three vertical asymptotes.
As matter of fact, its vertical asymptotes are found at $x=0$, $x = 3$, and $x = -4$.
Recall that when the function’s numerator and denominator share a common factor, $x – a$, $f(x)$ is said to have a hole at $x = a$.
b. Since $f(x)$’s numerator and denominator share a common factor of $x + 2$, it has a hole at $x = -2$. Once simplified, we can see that $x = 4$ is a vertical asymptote of $f(x)$.
We also know that when $\lim_{x\rightarrow a} f(x) = \infty$, $x = a$ is a vertical asymptote of $f(x)$.
c. This means that $f(x)$ has vertical asymptotes at $x = -3$ and $x = 4$.
Example 2
Identify the vertical asymptotes of $f(x) = \dfrac{x^3 – 8}{x^4 – 8x^2 + 16}$.
Solution
Express the numerator and denominator of $f(x)$ in their factored forms.
Recall that the difference of two cubes property is $a^3 – b^3 = (a-b)(a^2 +ab +b^2)$. We apply this factor the numerator and apply the perfect square trinomial property to factor the denominator.
| $ x^3 – 8$ | $(x – 2)(x^2 + 2x + 4)$ |
| $ x^4 – 8x^2 + 16$ | $(x^2 – 4)^2 = (x – 2)^2(x + 2)^2$ |
| $f(x) = \dfrac{(x – 2)(x^2 + 2x + 4)}{(x-2)^2(x+2)^2}$ | |
We can see that $x – 2$ is a common factor, so there is a hole at $x=2$. The remaining factor of the denominator can now then be equated to $0$ to find the vertical asymptotes of $f(x)$.
$ \begin{aligned}(x-2)(x+2)^2&=0\\x&=2\\x&=-2\end{aligned}$
This means that the function has vertical asymptotes at $x = -2$ and $x=2$.
Example 3
Identify the vertical asymptotes of $f(x) = \dfrac{x^2 – 1}{x^3 -6x^2 + 5x}$. Plot these asymptotes (any holes, if any) on the graph that is shown below.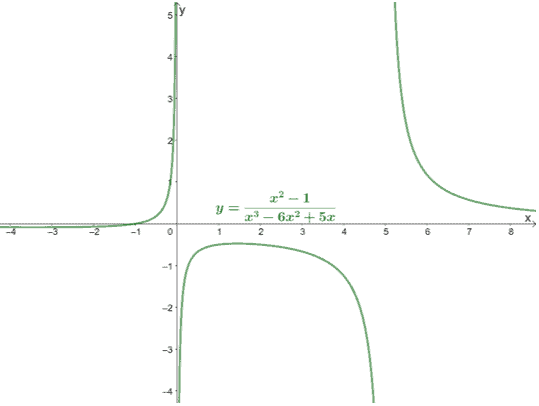
Solution
Let’s go ahead first and express the numerator and denominator of $f(x)$ in its factored form first.
$ \begin{aligned}x^2 – 1&= (x -1)(x +1)\\\\x^3 -6x^2 + 5x &= x(x^2 -6x + 5)\\&=x(x – 1)(x -5) \end{aligned}$
This means that we have $f(x) = \dfrac{(x -1)(x +1)}{ x(x – 1)(x -5)}$. Since $(x – 1)$ is a common factor shared by the numerator and denominator, $x = 1$ is a discontinuity. To find the $y$-coordinate of the hole, simplify $f(x)$ and substitute $x$ with 1.
$ \begin{aligned}f(x) &= \dfrac{\cancel{(x -1)}(x +1)}{x\cancel{(x -1)}(x -5)}\\&=\dfrac{x + 1}{x(x – 5)}\\\\f(1)&=\dfrac{1+1}{1(1-5)}\\&=\dfrac{2}{-4}\\&=-\dfrac{1}{2}\end{aligned}$
After simplifying $f(x)$, let’s equate the denominator’s remaining factors to $0$.
$\begin{aligned}f(x) &=\dfrac{x + 1}{x(x – 5)}\\\\ x(x-5)&=0\\x&=0\\x&=5\end{aligned}$
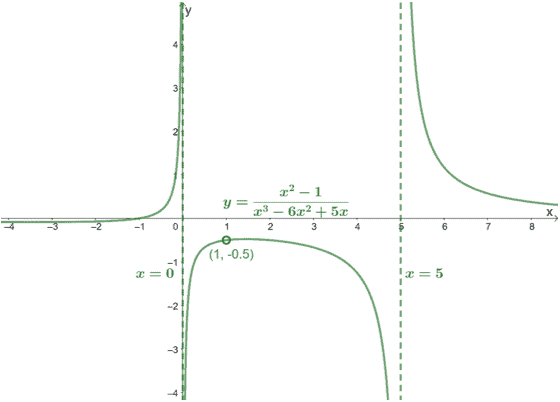
We can see that the function has vertical asymptotes at $x=0$ and $x= 5$.
Let’s go ahead and graph these two vertical asymptotes as vertical dashed lines. Plot an unfilled point at $\left(1, -\dfrac{1}{2}\right)$ as well.
Practice Questions
![]()
Images/mathematical drawings are created with GeoGebra.
