Algebraic Expression – Explanation & Examples

Algebra is an interesting and enjoyable branch of mathematics in which numbers, shapes, and letters are used to express problems. Whether you are learning algebra in school or examining a certain test, you will notice that almost all mathematical problems are represented in words.

Therefore, the need to translate written word problems into algebraic expressions arises when we need to solve them.

Most of the algebraic word problems consist of real-life short stories or cases. Others are simple phrases such as the description of a math problem. This article will learn how to write algebraic expressions from simple word problems and then advance to lightly complex word problems.

What is an Algebraic Expression?

An algebraic expression is a mathematical phrase where variables and constants are combined using the operational (+, -, × & ÷) symbols.  An algebraic symbol lacks the equal (=) sign. For example, 10x + 63 and 5x – 3 are examples of algebraic expressions.

Many people interchangeably use algebraic expressions and algebraic equations, unaware that these terms are totally different.

On the other hand, an algebraic is a mathematical phrase where two sides of the phrase are connected by an equal sign (=). For example, 3x + 5 = 20 is an algebraic equation where 20 represents the right-hand side (RHS), and 3x +5 represents the left-hand side (LHS) of the equation.

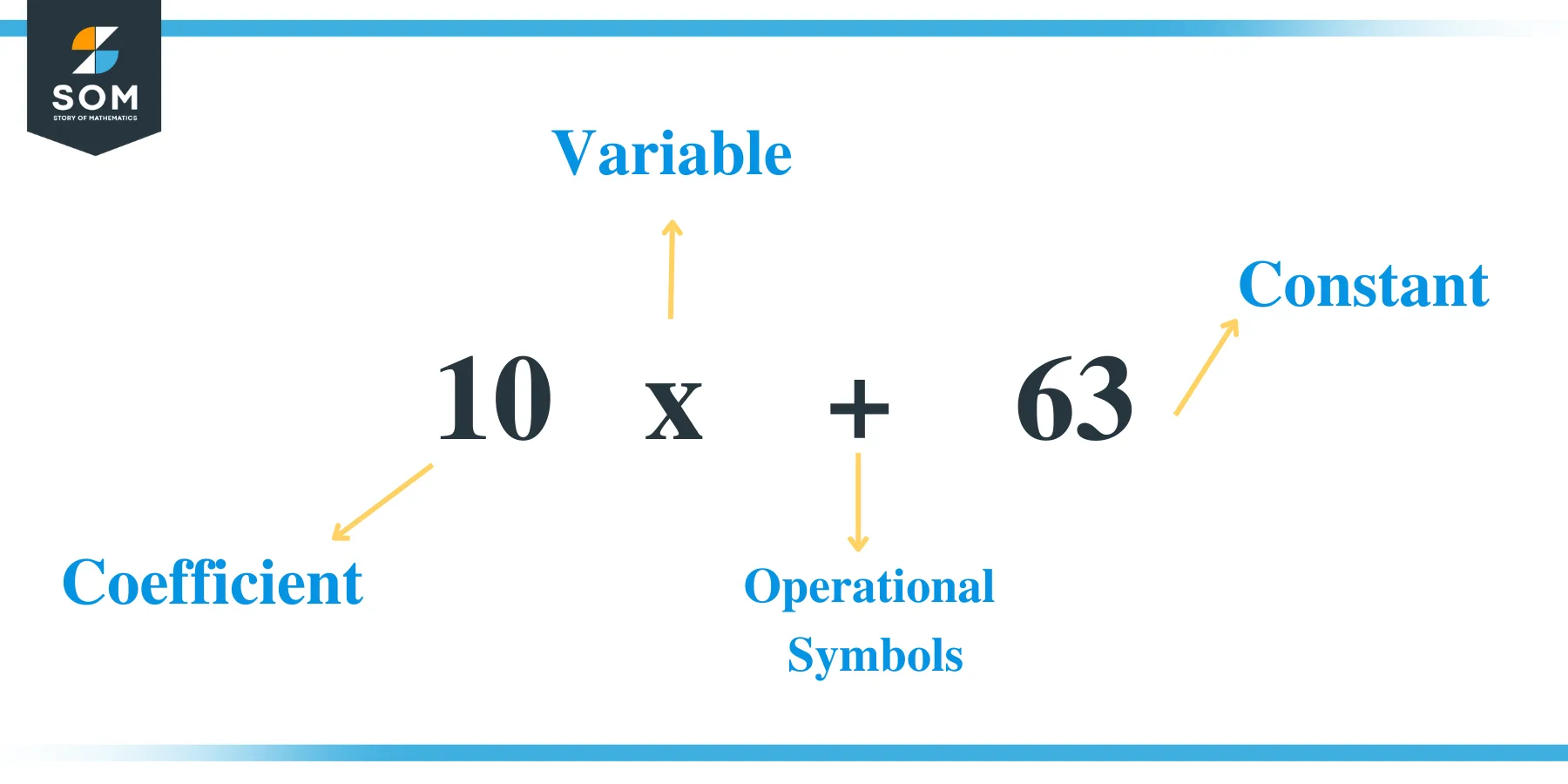
Let’s take a review of the terminologies used in an algebraic expression:

• A variable is a letter whose value is unknown to us. For example, x is our variable in the expression: 10x + 63.
• The coefficient is a numerical value used together with a variable. For example, 10 is the variable in the expression 10x + 63.
• A constant is a term that has a definite value. In this case, 63 is the constant in an algebraic expression, 10x + 63.

There are several types of algebraic expressions, but the main type includes:

• Monomial algebraic expression

This type of expression has only one term, for example, 2x, 5x ² ,3xy, etc.

• Binomial expression

An algebraic expression having two, unlike terms, for example, 5y + 8, y+5, 6y³ + 4, etc.

• Polynomial expression

This is an algebraic expression with more than one term and with non -zero exponents of variables. An example of a polynomial expression is ab + bc + ca, etc.

Other types of algebraic expressions are:

• Numeric Expression:

A numerical expression only consists of numbers and operators. No variable is added in a numeric expression. Examples of numeric expressions are; 2+4, 5-1, 400+600, etc.

• Variable Expression:

This expression contains variables alongside numbers, for example, 6x + y, 7xy + 6, etc.

How to Solve Algebraic Expression?

The purpose of solving an algebraic expression in an equation is to find the unknown variable. When two expressions are equated, they form an equation, and therefore, it becomes easier to solve for unknown terms.

To solve an equation, place the variables on one side and the constants on the other side. You can isolate the variables by applying arithmetic operations like addition, subtraction, multiplication, division, square root, cube root, etc.

An algebraic expression is always interchangeable. This implies that you can rewrite the equation by interchanging the LHS and RHS.

Example 1

Calculate the value of x in the following equation.

5x + 10 = 50

Solution

This given equation is 5x + 10 = 50.

• Isolate the variables and the constants;
• You can keep the variable on the LHS and the constants on the RHS.

5x = 50-10

• Subtract the constants;

5x = 40

Divide both sides by the coefficient of the variable;

x = 40/5 = 8

Therefore, the value of x is 8.

Example 2

Find the value of the y when 5y + 45 = 100.

Solution

Isolate the variables from the constants;

5y = 100 -45

5y = 55

Divide both sides by the coefficient;

y = 55/5

y= 11

Example 3

Determine the value of the variable in the following equation:

2x + 40 = 30

Solution

Separate the variables from the constants;

2x = 30 – 40

2x = -10

Divide both sides by 2;

x = -5

Example 4

Find t when 6t + 5 = 3.

Solution

Separate the constants from the variable,

6t = 5 -3

6t = -2

Divide both sides by the coefficient,

t = -2/6

Simplify the fraction,

t = -1/3