Angle of Depression – Explanation & Examples

When you look at an item below you, you can easily measure the angle of depression formed by your line of sight with the horizontal line. Just imagine you are standing at the top of the Tower of Pisa and looking at an infinite horizon to enjoy the beautiful weather on a great rainy day. Suddenly your friend on the ground accidentally sees you and screams to say “Hi.” You lower your eyes to look at your friend. You must realize that you created a certain angle as you look downwards toward your friend. This angle is called the angle of depression. 

The angle of depression is basically the measure of an angle between the horizontal line and line of sight of a person’s eyes to any item below. The angle of elevation depends upon the movement of your eyes. 

After this lesson, we expect you to learn the concepts of the angle of depression and be able to confidently explain what it is.

What Is an Angle of Depression?

When an observer is looking down at an object below him, the angle established by the line of sight with the horizontal line is called the angle of depression.

Let us consider a vertical wall with its base fixed to the ground as shown in Figure 12-1. Let’s say a man is standing some distance away from the wall and looking straight at it. The line drawn from the man’s perspective to the far point where the man is staring is known as the line of sight. Since this line is parallel to the ground, we call it the horizontal line of sight — or simply a horizontal line.

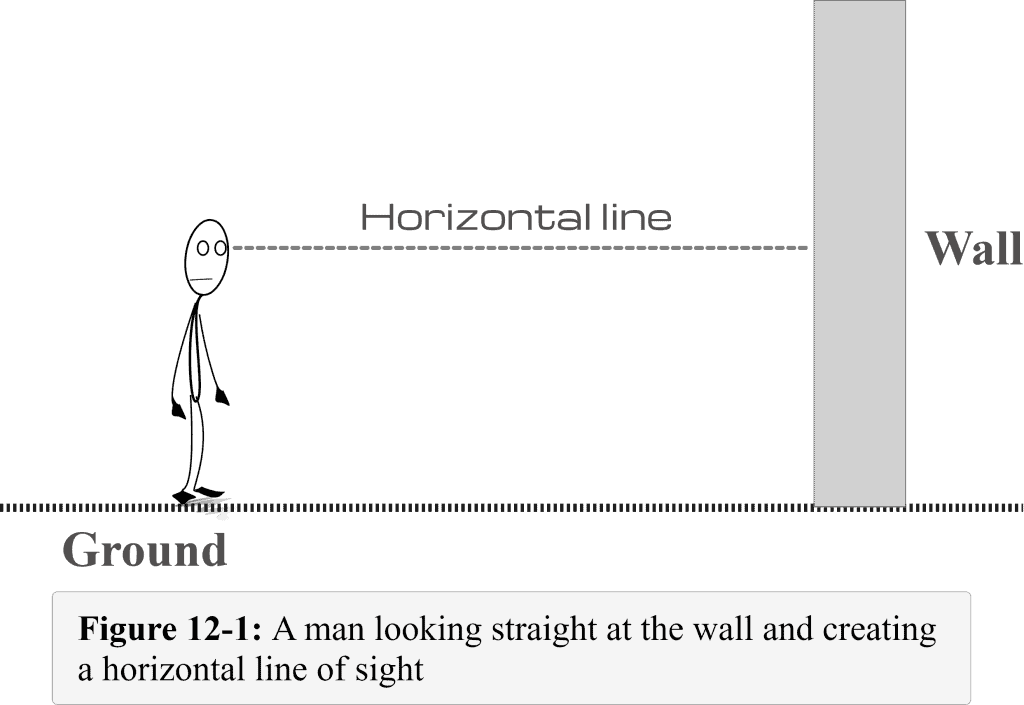
Now if the man is looking at the base of the wall, what should be the line of sight?

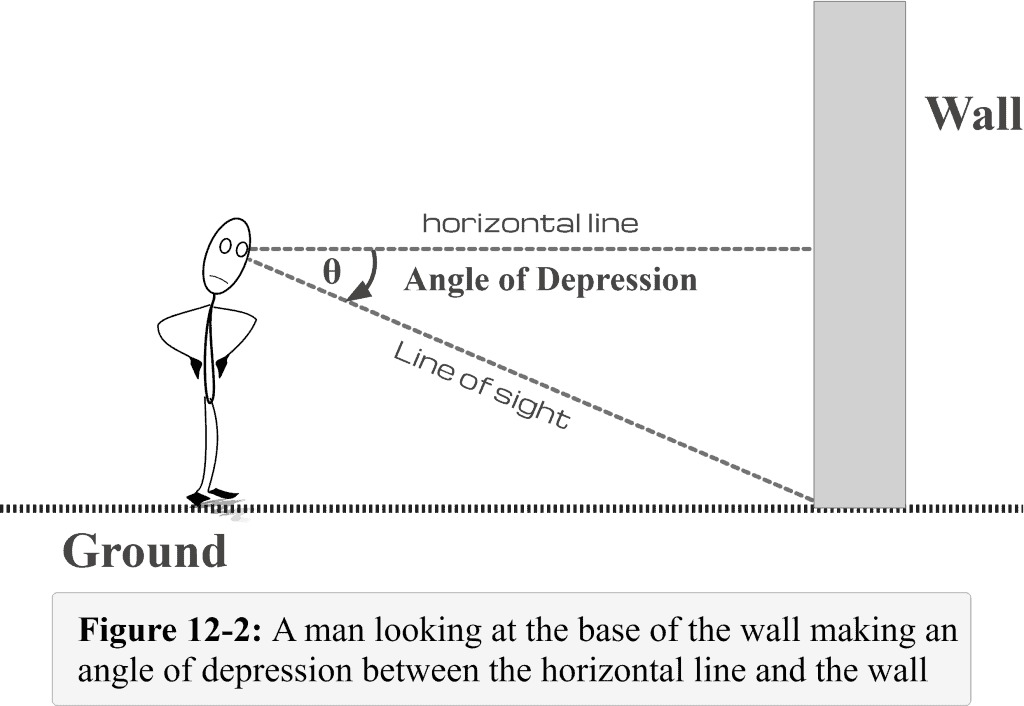
The above Figure 11-2 shows that the line drawn from the eye to the base of the wall would be the line of sight. We can easily observe that this line of sight (when looking down) makes an angle with the horizontal line. This angle is called the angle of depression. You need to ponder that the line of sight is below the horizontal line.

Looking at Figure 11-2, the angle $\theta$ represents the angle of depression.

How To Find the Angle of Depression

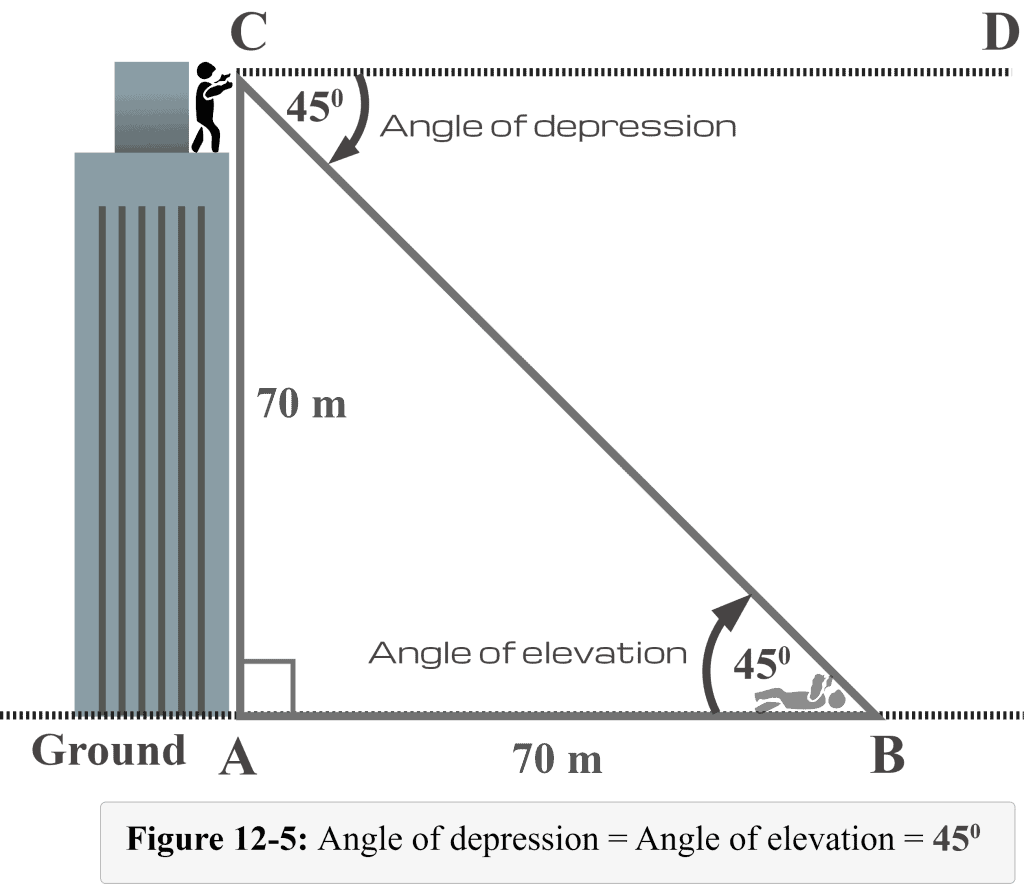
In Figure 11-3, Mr. Toni, from the top of the building, is seeing his friend lying on the ground to take a rest. The height of the building is $70$ m. His friend is $70$ m from the building. Let us determine the angle of depression between Toni’s line of sight (when looking downward) to his friend and the horizontal line drawn from Toni’s eyes.

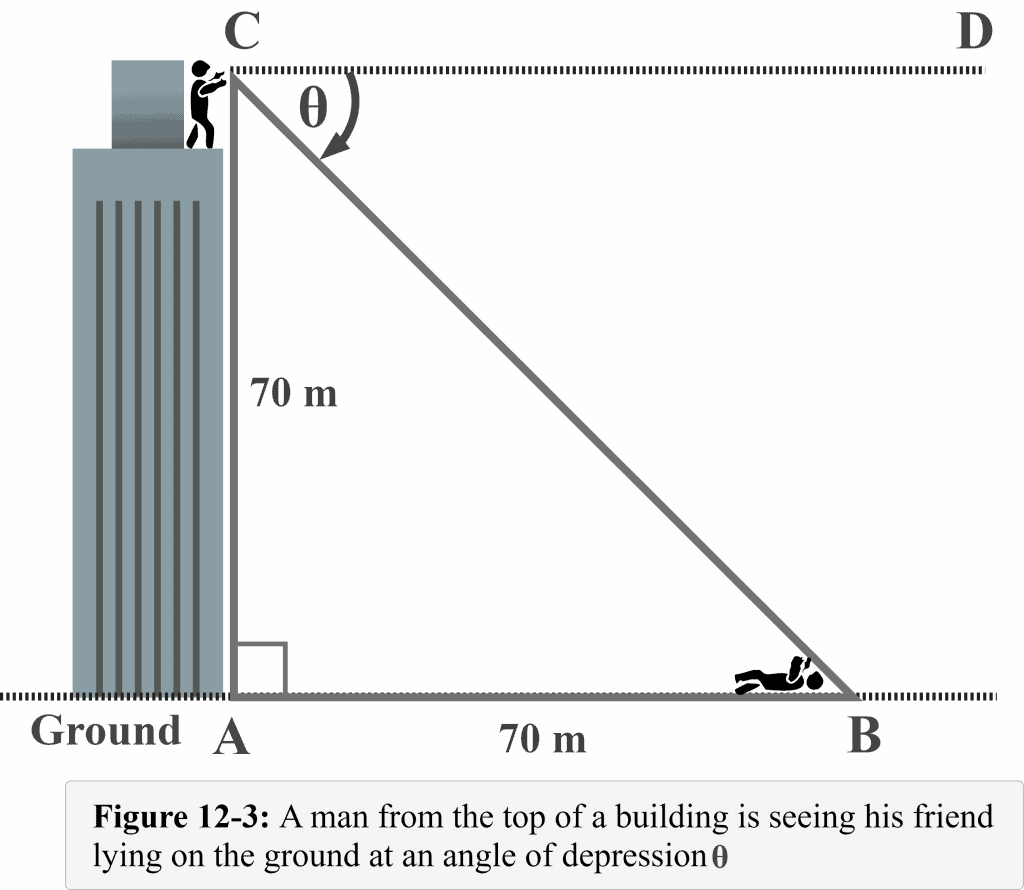
In this example, the angle $\theta$ represents the angle of depression between Mr. Toni’s line of sight (when looking downward) to his friend and the horizontal line. Note that the angle of depression is outside of the triangle and measured from the top, which is the ceiling. Also, the horizontal line is parallel to the ground surface.

Similarly, note that $∠CBA$ is an angle of elevation (discussed in our previous lesson) as it is measured from the ground, the angle with which Toni’s friend will be looking at him from the ground surface (another horizontal line).

Now, we have:

• Two parallel lines $CD$ and $AB$
• A line of sight $BC$ is the transversal

We must recall the geometry rule that when two parallel lines $AB$ and $CD$ are cut by a transversal line $BC$, we get the alternate interior angles which are angle $\theta$ (angle of depression) and $∠CBA$ (angle of elevation) in our case. We know that alternate interior angles are congruent. Thus,

Angle of depression $\theta =$ Angle of elevation $∠CBA$

Now utilizing this fact, we need to label $∠CBA$ as $\theta$ inside the triangle, as shown in Figure 12-4 below.

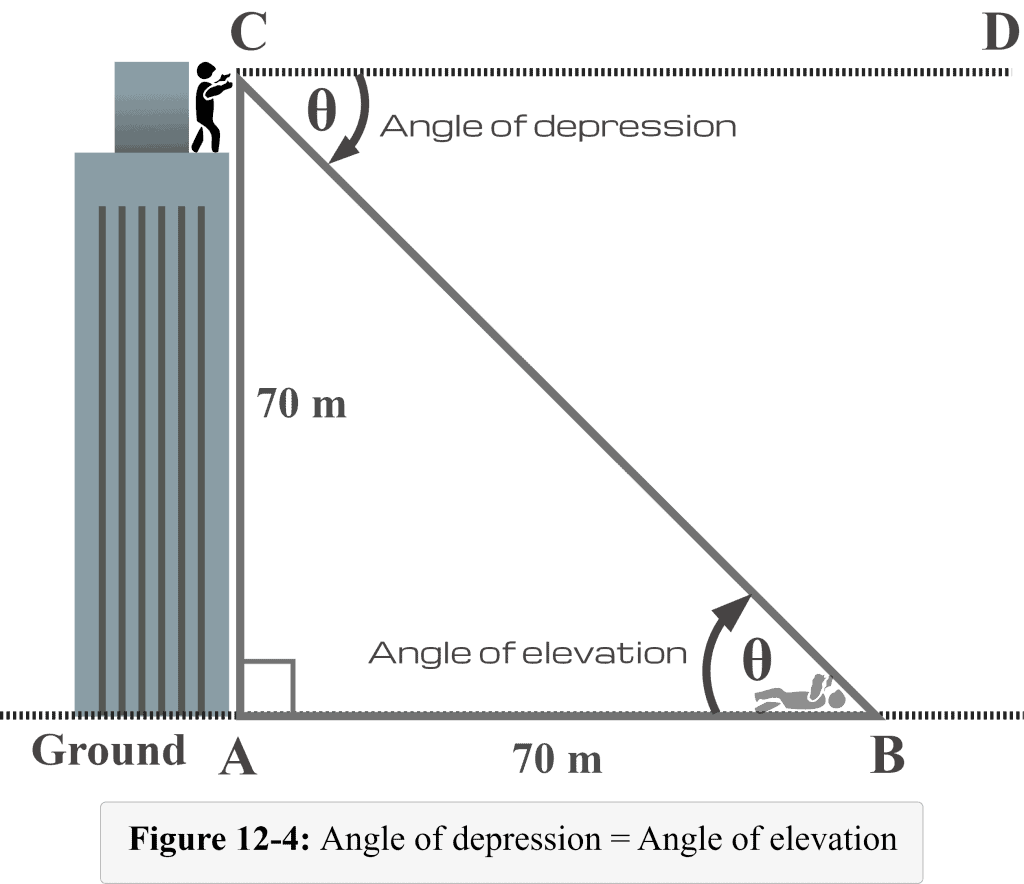
Now from the perspective of $m∠B = \theta$, we observe that:

Opposite side $AC = 70$ m

Adjacent side $AB = 70$ m

Using the formula of the tangent function

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite $= 70$, and adjacent $= 70$ in the formula

${\displaystyle \tan \theta ={\frac {70}{70}}}$

$\tan \theta = 1$

solving the equation

$\theta =\tan^{-1}(1)$

$\theta = 45^{\circ }$

We know that the angle of depression is equal to the angle of elevation.

Therefore, the measure of the required angle of depression θ is $\theta = 45^{\circ }$.

Figure 12-5 also illustrates the relationship between the angle of depression and the angle of elevation.

Summary

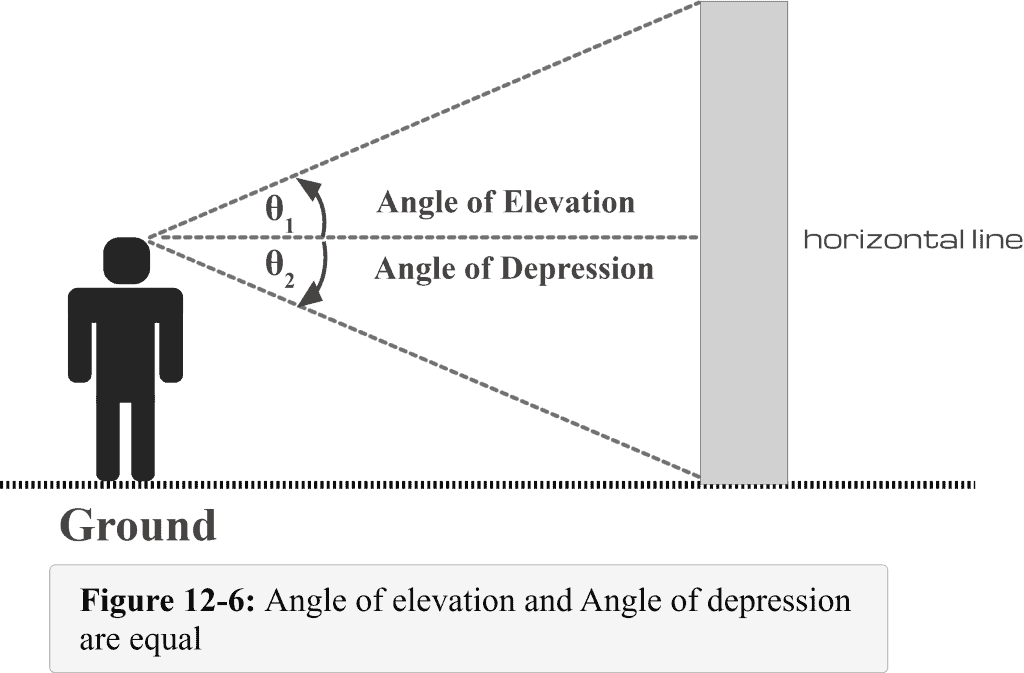
Figure 12-6 illustrates the summary of what we have discussed so far.

• When the light of sight is above the horizontal line, an angle of elevation is formed. 
• When the light of sight is below the horizontal line, an angle of depression is formed. 
• Angle of depression $\theta$₁ = Angle of elevation $\theta$₂

Example 1

From the top of a palm tree of length $18$ m, Mr. Toni observes the base of the building on the ground. If the building is at a distance of $20$ meters from the tree, what is the angle of depression of the building on the ground from the top of the tree? Assume that the tree is vertical.

Solution:

In this diagram, $\theta$ represents the angle of depression of the building on the ground from the top of the tree.

Take note that the horizontal line in the angle of the depression diagram is parallel to the ground surface, establishing the fact that alternate interior angles are congruent. Thus, the measure of the angle $\theta$ is equal to $m∠CBA$. In other words,

$m∠B = \theta$

The tree is vertical, making it perpendicular to the ground, so looking at the diagram, it is clear that a right triangle $ΔCAB$ is formed.

From the perspective of $m∠B = \theta$, we observe that:

Opposite side $AC = 18$ m

Adjacent side $AB = 20$ m

Using the formula of the tangent function:

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

substitute opposite = $18$, and adjacent = $20$ in the formula

${\displaystyle \tan \theta = {\frac {{18}}{20}}}$

$\tan \theta = 0.9$

solving the equation

$\theta =\tan^{-1}(0.9)$

$\theta = 41.9872125^{\circ }$

$\theta ≈ 42^{\circ }$ (Rounded to the whole number)

Therefore, the measure of the required angle of depression θ is approximately $42^{\circ }$.

Example 2

From the top of the building, Mr. Robertson sees his two friends, Friend $A$ and Friend $B$, on the ground at an angle of depression of $60^{\circ }$ and $30^{\circ }$, respectively, on the opposite sides of the building. The height of the building is $100$ m. Determine the distance between Friend A and Friend B.

Solution:

First, create a simple labeled diagram showing the known measurements and depicting the scenario as shown below.

Looking at the diagram, we can observe that:

$CO =$ Height of the building $= 100$ m

Friend $A$ is at position $A$, and friend $B$ is at position $B$.

The angle of depression $m∠DCB = 30^{\circ }$ and $m∠D’CA = 60^{\circ }$

In geometry, alternate interior angles are congruent.

$∠DCB ≅ ∠CBO$

$∠D’CA ≅ ∠CAO$

So,

$m∠CBO = 30^{\circ }$

$m∠CAO = 60^{\circ }$

The distance $AB$ between Friend $A$ and Friend $B = AO + BO$

In the right-angled triangle $⊿COA$,

${\displaystyle \tan 60^{\circ } = {\frac {{CO}}{AO}}}$

$\sqrt{3} = {\frac {{100}}{AO}}$

$AO = {\frac {{100}}{\sqrt{3}}}$

In the right-angled triangle $⊿COB$,

${\displaystyle \tan 30^{\circ } = {\frac {{CO}}{BO}}}$

${\frac {{1}}{\sqrt{3}}} = {\frac {{100}}{BO}}$

$BO = 100\sqrt{3}$

Thus,

The distance $AB$ between Friend $A$ and Friend $B = AO + BO$

                                                                                           $= {\frac {{100}}{\sqrt{3}}} + 100\sqrt{3}$

                                                                                           $= {\frac {{100+300}}{\sqrt{3}}}$

                                                                                            $= {\frac {{400}}{\sqrt{3}}}$

                                                                                            $= {\frac {{400}}{1.73205}}$

                                                                                            $≈ 230.9$ m (Rounded to the nearest $0.01$)

Therefore, the distance between Friend $A$ and Friend $B$ is approximately $230.9$ m.

Example 3

From the top of a larger building, Mr. Jordan observes the top and the base of the smaller building at the angle of depression of $30^{\circ }$ and $60^{\circ }$, respectively. The height of the larger building is $60$ m. What is the height of the smaller building?

Solution:

Looking at the diagram, we observe that:

Height of the larger building $AB = 60$ m

The angle of depression of the top of the smaller building is $30^{\circ }$, as observed from the top of the larger building.

Thus,

$m∠EAC = 30^{\circ }$

The angle of depression of the base/foot of the smaller building is $60^{\circ }$, as observed from the top of the larger building.

Thus,

$m∠EAD = 60^{\circ }$

Also

$AB = ED = 60$ m

Let the height of smaller building $CD = h$

Thus,

$CE = 60 – h%%EDITORCONTENT%%nbsp;        ∵ $AB = ED = 60$ and $ED = CD + CE$

As $AE$ is parallel and equal to $BD$

$AE = x$

In the triangle $△EAC$,

${\displaystyle \tan 30^{\circ } = {\frac {{CE}}{AE}}}$

${\frac {{1}}{\sqrt{3}}} = {\frac {{(60-h)}}{x}}%%EDITORCONTENT%%nbsp;   — $[1]$

$BO = 100\sqrt{3}$

In the triangle $△EAD$,

${\displaystyle \tan 60^{\circ } = {\frac {{ED}}{AE}}}$

$\sqrt{3} = {\frac {{60}}{x}}%%EDITORCONTENT%%nbsp;   — $[2]$

Dividing equation $1$ by $2$, we get

$\frac{\frac{\left(60-h\right)}{x}}{\frac{60}{x}}=\frac{\frac{1}{\sqrt{3}}}{\sqrt{3}}$

$\frac{\left(60\:-\:h\right)}{60}\:=\:\frac{1}{3}$

$3\left(60\:-\:h\right)=60$

$180\:-\:3h\:=\:60$

$3h=180-60$

$3h = 120$

Divide both sides of the equation by $3$

$h = 40$ m

Therefore, the height of the smaller building is $40$ m.