Applications of Trigonometry – Explanation & Examples

The origin of trigonometry may have been traced to the ancient civilization of Egypt and Mesopotamia — around 4000 years ago — but it has assumed unprecedented importance in a modern world, expanding its applications into numerous fields such as surveying, astronomy, computer science, architecture, Physics, archaeology, video games, and navigation, etc. Can you imagine measuring the height of the K-2 mountain without climbing it? It may sound crazy, but trust me, you can do it. This is the beauty of Trigonometry — simple but powerful. 

Trigonometry has the special trait of having various real-world applications across many fields. The techniques used in trigonometry help us to crack incredibly complex design problems to solve real-life applications.

After reading this guide, you will be able to understand the importance and application of trigonometry in our day-to-day lives.

What Is Trigonometry Used For?

Trigonometry is used for many purposes across different fields such as Architecture, construction, Astronomy, music, etc. People all over the world use this mathematical concept to achieve different outcomes, and you might even be using trigonometry without realizing it!

Trigonometry is simply the study of triangles, but it has several practical applications. Suppose you want to determine how tall a tower is, navigate the solar system to determine how far the sun is from earth or the distance between planets and stars, build state-of-the-art buildings, measure the height of ocean tides, etc. In that case, you must know how to use trigonometry. Without the knowledge of trigonometry, modern industrial mechanisms and sciences simply cannot exist.

Here are few examples where trigonometry plays a very important role in solving problems right from the basic level to more complex real-world applications.

Architecture

With the help of trigonometry, we are able to witness some of the most iconic building structures like Burj Al Khalifa Hotel, Pisa Tower, Petronas Tower, Taj Mahal, St. Paul Cathedral, London, and Empire State Building, etc. Without trigonometry, we will not be able to witness these masterpieces.

Construction

While trigonometry is used to design buildings, its role in construction cannot be underestimated. It is very important to determine the roof slopes, the appropriate height, and load balance using certain mathematical methods.

Astronomy

The incredible framework of our beautiful solar system has always captivated human beings since the start of civilization. Trigonometry has helped scientists, engineers, and astronomers to determine the distance between the earth and other planets and stars, helping them manufacture and launch space rockets.

Today, we are on the verge of exploring the new life on Mars, and in the past, humans have been able to reach the moon. Without trigonometry, we cannot even think about these possibilities.

Game Development

You must have at least a basic understanding of trigonometry if you want to create your own game. If you’re going to design the game environment, create game characters and make them move across the platform, you must know how to use trigonometry.

Music

If you are a musician and want to produce outstanding music production, trigonometry is your best friend. You can generate your own sounds by manipulating sine waves. Understanding the workings of notes, chords, and sine waves will help you generate the desired sound.

The Distance and Height Measurement

Whether you want to determine the height of a mountain or need to calculate how far you are standing from a building, you need to learn trigonometry. If you know a little piece of information, you can use the power of trigonometry to measure the unmeasurable calculations otherwise.

Here are some of the other fields where trigonometry plays a vital role to solve complex real-life applications:

• Navigation
• Marine engineering
• Flight engineering
• Criminology
• Navigation
• Cartography
• Aviation industry
• Satellite systems
• Creation of maps

Example 1

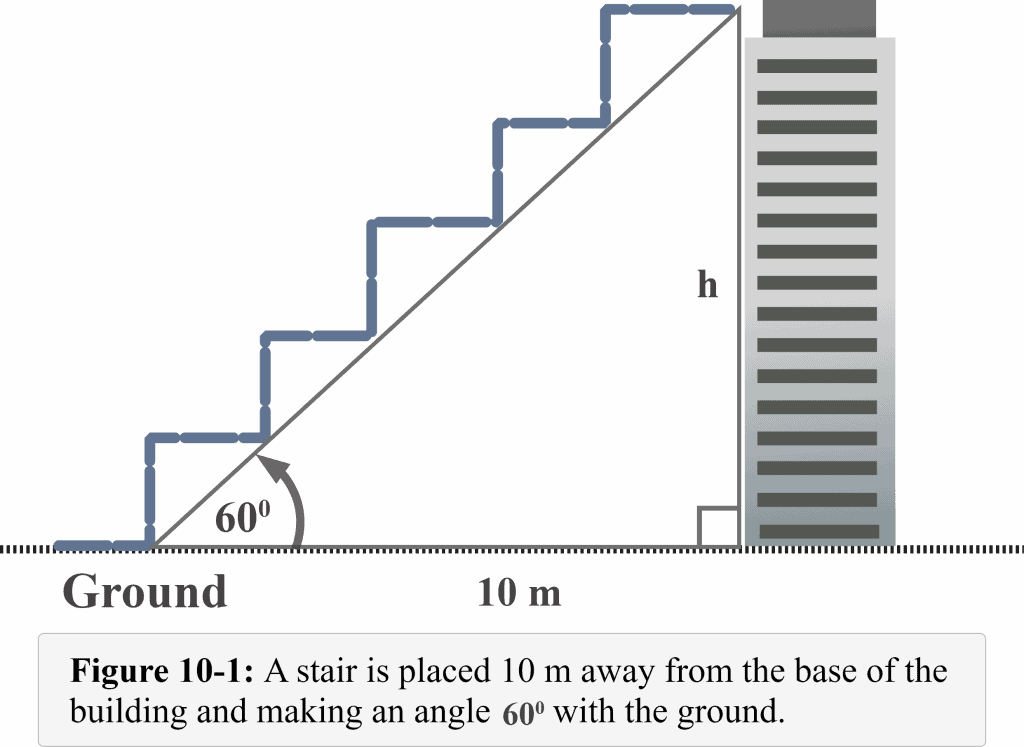
Figure 10-1 displays a very large staircase placed $10$ m from the base of the building and makes an angle of $60^{\circ }$ as measured from the ground to the top of the building. Mr. David wants to reach the top of a building using this staircase. What is the height of the building?

Solution:

In our stair example, the side of length $10$ m is the adjacent side that lies right next to the reference angle $60^{\circ }$.

Observe that the height h of the building lies exactly opposite the reference angle $60^{\circ }$.

Thus, we have:

Adjacent $= 10$ m

Opposite $= h$

$\theta = 60^{\circ }$

We know that the tangent function is the ratio of the opposite side to the adjacent side.

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

Substituting adjacent $= 10$, $\theta = 60^{\circ }$ and opposite $= h$ in the formula:

${\displaystyle \tan 60^{\circ } = {\frac {\mathrm {h} }{\mathrm {10} }}}$

$\sqrt{3} = {\frac {\mathrm {h} }{\mathrm {10} }}$

$h = \sqrt{3} (10)$

$h ≈ 17.3 m$

Therefore, the height of the building is approximately $h ≈ 17.3 m$.

Example 2

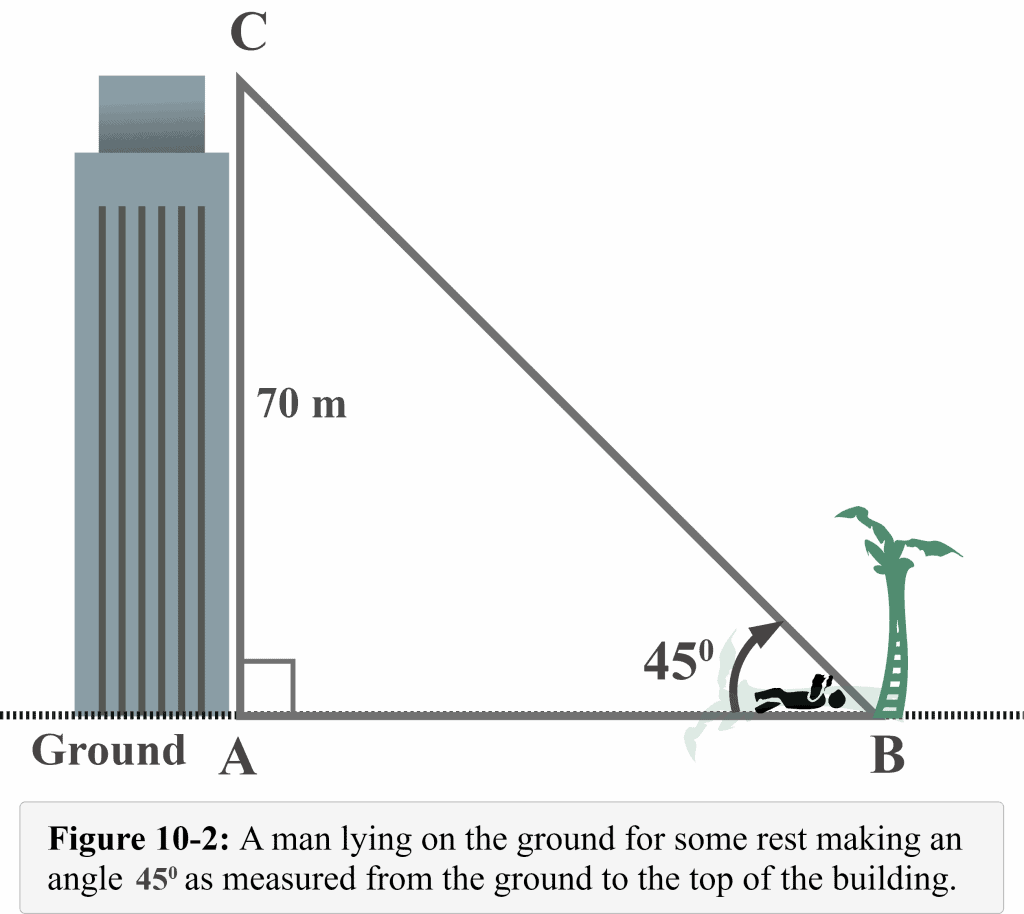
Figure 10-2 shows a man lying on the ground under the tree’s shade to take some rest and makes an angle of $45^{\circ }$ as measured from the ground to the top of the building. The height of the building is $70$ m. Determine the distance of the lying man from the building.   

Solution:

In our example, the side of height $70$ m is the opposite side that lies exactly opposite the reference angle $45^{\circ }$.

The side $AB$ represents the distance of the lying man from the building. Thus, we have to measure the side $AB$.

Clearly, the side $AB$ is the adjacent side that lies right next to the reference angle $60^{\circ }$.

Thus, we have:

Opposite $= AC = 70$ m

$\theta = 45^{\circ }$

Adjacent $= AB$

We know that the tangent function is the ratio of the opposite side to the adjacent side.

${\displaystyle \tan \theta ={\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

Substituting opposite $= 70$, $\theta = 45^{\circ }$ and adjacent $= AB$ in the formula:

${\displaystyle \tan 45^{\circ } = {\frac {\mathrm {70} }{\mathrm {AB} }}}$

$1 = {\frac {\mathrm {70} }{\mathrm {AB} }}$

$AB = 70$ m

Therefore, the distance of the lying man from the building is $70$ m.

Example 3

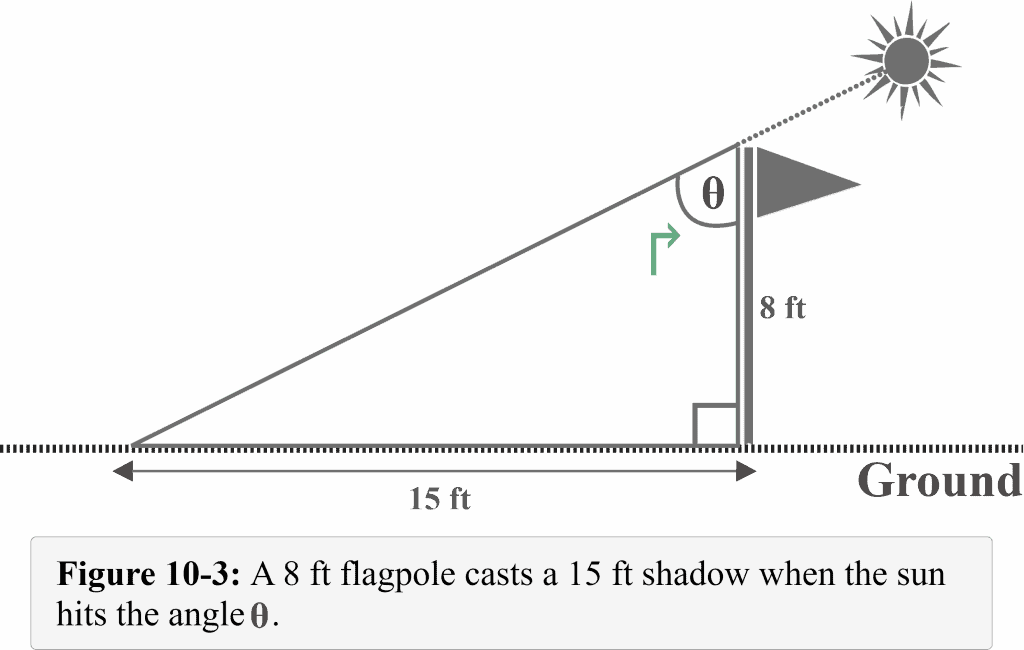
A flag of height $8$ feet casts a $15$ feet shadow as shown in Figure 10-3. Determine the measure of an angle $\theta$ that the sun hits the flagpole.

Solution:

In our example, the side of length $8$ feet is the adjacent side that lies right next to the reference angle $\theta$, and the side of length 15 feet lies exactly opposite the reference angle $\theta$.

We have to measure the angle $\theta$ that the sun hits the flagpole.

Thus, we have:

Adjacent $= 8$ feet

Opposite $= 15$ feet

$\theta =?$

We know that the tangent function is the ratio of the opposite side to the adjacent side.

${\displaystyle \tan \theta = {\frac {\mathrm {opposite} }{\mathrm {adjacent} }}}$

Substituting adjacent $= 8$, opposite $= 15$ in the formula:

${\displaystyle \tan \theta = {\frac {\mathrm {15} }{\mathrm {8} }}}$

$\tan \theta = 1.875$

$\theta = \cos^{-1} (1.875) $

$\theta = 61.9275131…^{\circ }$

$\theta ≈ 61.9^{\circ }$

Therefore, the measure of an angle θ that the sun hits the flagpole is $61.9^{\circ }$.

Who Uses Trigonometry?

Architects, Astronomers, Engineers, and Archaeologists are just some professionals that use trigonometry in their daily lives. Aside from them, a lot of other people working in different fields also employ this subject.

Architecture and Engineers

It is essential to correctly layout a curved wall and measure the accurate gradient of a roof or the precise height and rise of the staircase to do the job correctly. Architectures and Engineers use trigonometry to solve complex calculations to build iconic buildings. Without trigonometry, it would have been impossible to create the masterpiece that are buildings.

Astronomers

Trigonometry plays a very crucial role in the field of Astronomy. Astronomers need to use trigonometry to figure out how far certain stars and planets are from other life-like planets like Earth and Mars. Without trigonometry, it would have been impossible for astronomers and scientists to even think about reaching the moon and Mars, etc.

Game and Software Engineers

Software engineers and computer scientists use trigonometry to create games. They use trigonometry to design game environments and code the motion interactions of the game characters to move across the environment.

Musicians

Musicians use trigonometry to produce outstanding music production. With the help of trigonometry, they can manipulate sine waves to create their own sounds.

Archeologists

Archeologists use trigonometry to calculate the distance from underground water systems.

Marine Biologists

Marine Biologists use the power of trigonometry to determine the behavior of underwater animals using specific mathematical models.

In a nutshell, trigonometry is used by various experts across different fields to solve the mysteries of real-life situations.