Area Under the Curve – Definition, Types, and Examples

One of the most useful applications of integral calculus is learning how to calculate the area under the curve. Definite integrals and areas found under the curve are essential in physics, statistics, engineering, and other applied fields. Learning about areas under the curve also makes you appreciate what you’ve learned so far and makes you see how amazing integral calculus is.

Areas under the curve are formed with the function, two vertical lines, and the horizontal axis. Their values can be calculated by evaluating the definite integral of the function with respect to the vertical bounds.

By the end of our discussion, you should be able to calculate the following:

• The area of the region completely lying above the $x$-axis.
• The area of the region below the curve and the $x$-axis.
• The area of the region below the curve where a part is located above and below the $x$-axis.

Since this topic is an application of integral calculus, review your knowledge of the definite integral and the fundamental theorem of calculus. Warm-up on integration and keep your notes on antiderivative formulas and properties nearby. For now, let’s learn how areas under the curve are represented on the $xy$-plane!

What is the area under the curve?

The area under the curve is defined as the region bounded by the function we’re working with, vertical lines representing the function’s bounds, and the $\boldsymbol{x}$-axis.

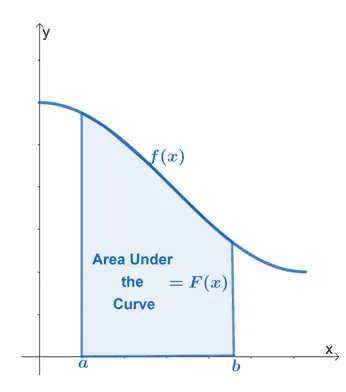
The graph above shows the area under the curve of the continuous function, $f(x)$. The interval, $[a, b]$, represents the vertical bounds of the function. The region has to be bounded by the $x$-axis all the time.

Now, what happens if the curve is found below the $x$-axis or passes through above and below the $x$-axis?

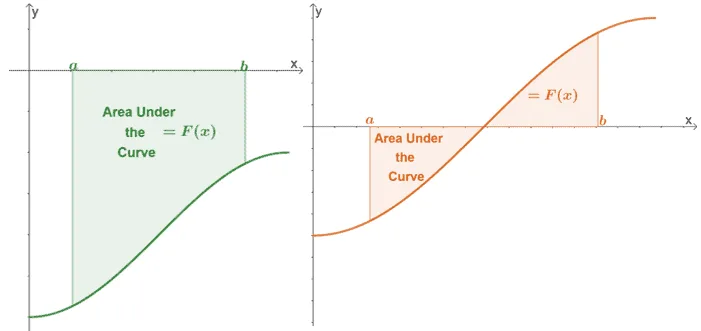
These two graphs are examples of functions’ curves that are not completely lying above the horizontal axis, so when this happens, focus on finding the region that is bounded by the horizontal axis.

In the past, we’ve learned that we can estimate the area under the curve through the Riemann sum and other approximation techniques. We can find the actual value of the area found under the curve by evaluating the integral of the function at the bounds of its interval.

\begin{aligned}\text{Area} &= \int_{a}^{b} f(x)\phantom{x} dx\\ &= F(b) – F(a)\end{aligned}

Keep in mind that $F(x)$ represents the antiderivative of $f(x)$. This means that when we want to find the area below $f(x)$’s curve and bounded by $x =a$ and $x =b$ as well as the $x$-axis, simply evaluate $f(x)$’s definite integral for the interval, $[a, b]$.

How to find the area under a curve?

When calculating the area under the curve of $f(x)$, use the steps below as a guide:

Step 1: Graph $f(x)$’s curve and sketch the bounded region. This step can be skipped when you’re confident with your skills already.

Step 2: Set the boundaries for the region at $x=a$ and $x =b$.

Step 3: Set up the definite integral. Separate the definite integrals found above and below the $x$-axis.

Step 4: Evaluate the definite integral. Take the absolute value if the region is found below the $x$-axis.

We’ll show you three examples covering all possible positions of the region: 1) area under the curve found above the $x$-axis, 2) area found below the $x$-axis, and 3) area found at both regions.

Head over to these three examples below to better understand how we implement the steps for each case. When you’re ready, you can also work on our practice questions to test your knowledge further.

Example 1

Find the area bounded by the curve of $f(x) = 4 – x^2$ from $x =-2$ to $x =2$.

Solution

Begin by sketching the graph to confirm that the area is located above the $x$-axis.

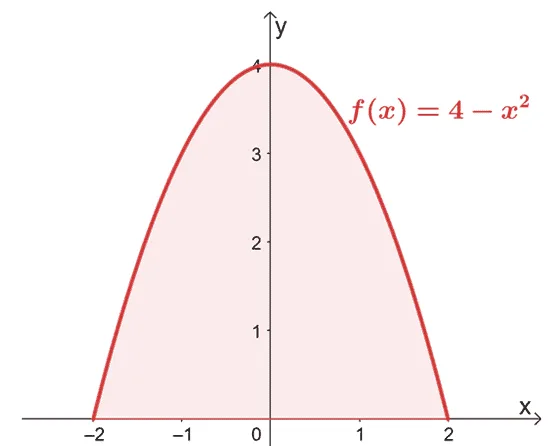
 Since the graph confirms that the entire region we need to account for is located above the $x$-axis, we simply evaluate the definite integral of $f(x)$ from $x = -2$ to $x =2$.

\begin{aligned}\text{Area} &= \int_{-2}^{2} (4 –x^2) \phantom{x}dx\end{aligned}

Apply the integral properties we’ve learned in the past to evaluate this expression. Once we have the antiderivative of $f(x)$, evaluate it from $x = -2$ and $x =2$.

\begin{aligned}\int (4 – x^2)\phantom{x}dx &= \int 4\phantom{x}dx – \int x^2\phantom{x}dx\\&= 4x – \dfrac{x^{2 + 1}}{2 + 1} + C\\&= 4x – \dfrac{x^3}{3} +C\\\\\text{Area} &=  \left[4x – \dfrac{x^3}{3} \right ]_{-2}^{2}\\&= \left[4(2) – \dfrac{2^3}{3}\right] – \left[4(-2) – \dfrac{(-2)^3}{3}\right]\\&= \dfrac{32}{3}\end{aligned}

From this, we can see that the area under the curve of $f(x)$ from $x = -2$ and $x = 2$ is equal to $\dfrac{32}{3}$ squared units.

Example 2

A great example for the second case is by finding the area bounded by the curve of $g(x) = x^2 – 9$ from $x = -3$ to $x =3$.

Solution

Graph the curve of $g(x)$ from $x = -3$ to $x = 3$. This will confirm whether the entire area is located entirely below the $x$-axis.

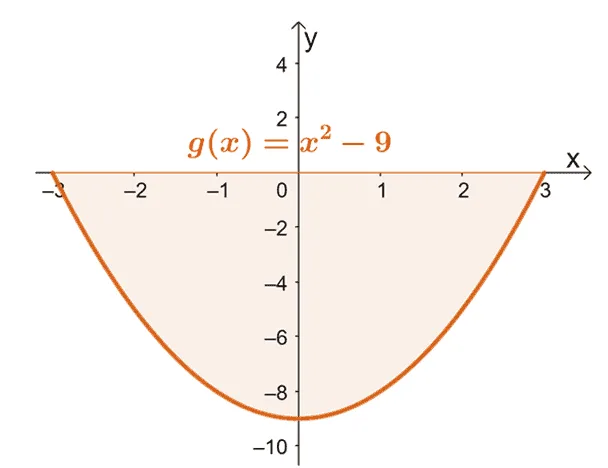
From this, we can see that the entire region bounded by the curve, $x = -3$, $x =3$, and the horizontal axis is found below the $x$- axis. This means that after evaluating the definite integral, we take the absolute value of the result to find the area under the curve.

\begin{aligned}\text{Area} &= \left|\int_{-3}^{3} (x^2 – 9) \phantom{x}dx\right|\end{aligned}

Find the antiderivative of $g(x)$ then evaluate the resulting expression at the bounds: $x =-3$ and $x = 3$.

\begin{aligned}\int (x^2 – 9)\phantom{x}dx &= \int x^2 \phantom{x}dx – \int 9 \phantom{x}dx\\&= \dfrac{x^{2 +1}}{2 + 1} – 9x + C\\ &= \dfrac{x^3}{3} – 9x + C\\\\\text{Area} &= \left|\left[ \dfrac{x^3}{3} – 9x  \right ]_{-3}^{3}\right|\\&= \left|\left[ \dfrac{(3)^3}{3} – 9(3)  \right ]-\left[ \dfrac{(-3)^3}{3} – 9(-3)  \right ]\right|\\&= |-36|\\&= 36\end{aligned}

The reason why we take the absolute value of the definite integral is to make sure that we return a positive value for the area. Hence, the area of the curve under $g(x)$ from $x=-3$ to $x=3$ is $36$ squared units.

Example 3

Find the area under the curve of $h(x)=x^3$ from $x=-2$ to $x=2$.

Solution

Let’s graph the curve of $h(x)=x^3$ and the area bounded by the intervals and the horizontal axis.

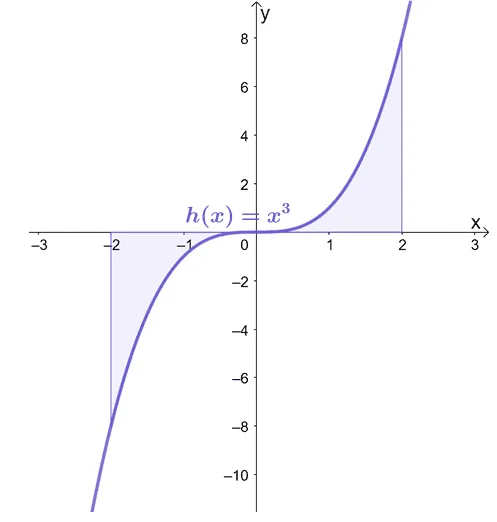
From the graph, we can see that the area is below the $x$-axis from $x= -2$ to $x=0$ and above the $x$-axis from $x= 0$ and $x =2$. Enclose the definite integral from $x=-2$ to $x =0$ with an absolute value.

\begin{aligned}\text{Area} &= \left|\int_{-2}^{0} x^3\phantom{x}dx\right| + \int_{0}^{2} x^3\phantom{x}dx\end{aligned}

Using the power rule for integrals, we have $\int x^3 \phantom{x} dx = \dfrac{x^4}{4} + C$. Now that we have the antiderivative of $h(x)$, evaluate each definite integral by evaluating $\dfrac{x^4}{4}$ at the given intervals.

\begin{aligned}\text{Area} &= \left|\left[\dfrac{x^4}{4} \right ]_{-2}^{0}\right|  + \left[\dfrac{x^4}{4} \right ]_{0}^{2}\\&= \left|\left[\dfrac{0^4}{4} – \dfrac{(-2)^4}{4} \right ]\right| + \left[\dfrac{0^4}{4} – \dfrac{(2)^4}{4} \right ]\\&= |-4| + 4\\&= 8\end{aligned}

The absolute value on the first definite integral ensures that we account for the area found below the horizontal axis. This means that the area under the curve of $h(x)$ from $x= -2$ to $x = 2$ is $8$ squared units.

Practice Questions

1. What is the area under the curve of $f(x)= 64 – x^2$ over the interval $4 \leq x \leq 8$?
2. Find the area under the curve of $g(x)= x^2 – 16$ from $x=-3 $ to $x= 3$.
3 What is the area under the curve of $h(x)=2x^3$ over the interval $-2 \leq x \leq 5$?
4. Find the area under the curve of $f(x)= \sqrt{x}$ from $x=0$ to $x=4$?
5. What is the area under the curve of $g(x)= \cos x$ over the interval $-\pi \leq x \leq 0$?

6. Find the area under the curve of $h(x)= \dfrac{x}{x^2 + 4}$ from $x=-4$ to $x=4$.

Answer Key

1. $\int_{4}^{8} (64 – x^2)\phantom{x}dx = \dfrac{320}{3}$ squared units
2. $\left|\int_{-3}^{-3} (x^2 – 16)\phantom{x}dx\right| = 78$ squared units
3. $\left|\int_{-2}^{0} x^3\phantom{x}dx\right| + \int_{0}^{5} x^3\phantom{x}dx = 320.5$ squared units
4. $\int_{0}^{4} \sqrt{x}\phantom{x}dx = \dfrac{16}{3}$ squared units
5. $\left|\int_{-pi}^{-\frac{\pi}{2}} \cos x \phantom{x}dx\right| + \int_{-\frac{\pi}{2}}^{0} \cos x\phantom{x}dx = 2$ squared units
6. $\left|\int_{-4}^{0} \dfrac{x}{x^2 + 4}\phantom{x}dx\right| + \int_{0}^{4} \dfrac{x}{x^2 + 4}\phantom{x}dx = \ln 5 \approx 1.609$ squared units

Images/mathematical drawings are created with GeoGebra.