Basic Algebra – Explanation & Examples

Algebra? The mere mention of the term makes most of the students break out in a cold sweat. There is this notion that algebra is the hardest course in mathematics.

This is just a mere fallacy, and in fact, algebra is one of the easiest topics in mathematics. This article is meant to alleviate this fear and misconception from students and make algebra an enjoyable lesson for beginners.

What is Algebra?

Have you ever wondered or asked yourself, what is algebra? Where did it originate from? How is algebra applied in real-life situations? Don’t worry. This article will take you step by step in understanding algebra and solve a few algebraic problems.

Basically, students will start their mathematical journey by learning to perform basic operations such as addition and subtraction. From there, a student will advance to multiplication and then to division. Later or sooner, a student will reach a point where they can tackle complex problems. What are we talking about? Algebra, of course!

Some people wrongly refer to algebra as the operation which deals with letters and numbers. In fact, Algebra was in existence before the invention of the printing press more than 2500 years ago. The introduction of printing initiated the use of symbols in algebra. Therefore, Algebra is well defined as the use of mathematical equations to model ideas. We model ideas in the form of mathematical equations to solve the problems around us.

History of Algebra

The word algebra originates from the Arabic word al-Jabr, which means placing broken parts together. This term is featured in the book “The Compendious Book on Calculation by Completion and Balancing” by Al-Khwarizmi, a Persian mathematician and astronomer. In the fifteenth century, algebra was initially used to describe a surgical procedure where dislocated, broken bones are reunited. From this discussion, we can say algebra helps us to reunite bits of information.

Why do we Need to Study Algebra?

Understanding algebra is fundamentally important to the student both in class and outside class. Algebra sharpens the reasoning ability of a student. Students can succinctly and systematically solve mathematical problems.

Let’s take a look at some of the importance of algebra in real life.

• A toddler or infant can apply algebra by tracing a trajectory of moving objects using eyes. Similarly, babies can estimate the distance between them and a toy and thus able to grab it. Therefore, small babies apply algebra despite the fact of lacking knowledge of algebra.
• Algebra is applied in computer science to write algorithms of programs. Algebra is also used in engineering to calculate correct proportions to implement a masterpiece. Maybe you will see these later when you advance your career.
• You require algebra to know when you are supposed to wake up and do morning chores or prepare for classes.
• Have you ever thrown dirt in a bin? Did you miss, or you made a perfect shot? You need algebra to estimate the distance between you and the trash bin and estimate the air resistance.
• The use of algebra calculates profits and losses in business. For this reason, good knowledge of algebra is essential for managing your finances.
• Algebra is widely applied in sports. For example, a goalkeeper can dive at a ball by estimating the speed of a ball. An athlete can also increase his/her pace by estimating the distance between them and the finish line.
• Algebra finds itself in the kitchen, such as cooking, mixing ingredients, and determining the cooking duration.
• Applications of algebra are just endless. That phone you are using, the computer games you are playing are just fruits of algebra. Computer graphics are developed on algebra.

How to do Algebra?

You will usually see both known values and unknown values in an algebraic expression, and you solve the equation for an unknown value. To solve that equation, you need to do algebra, in which you need to follow the same order of operations you do for the integers.

For example, you will first solve what is inside the parenthesis, then go for the following operations in sequence: exponents, multiplication, division, addition, and subtraction.

The following are the term which you will see in an algebraic expression.

• An equation is a statement or sentence that defines two identities separated by an equal (=) sign.
• Expression is a list or a group of different terms usually separated by ‘+’ or ‘- ‘sign

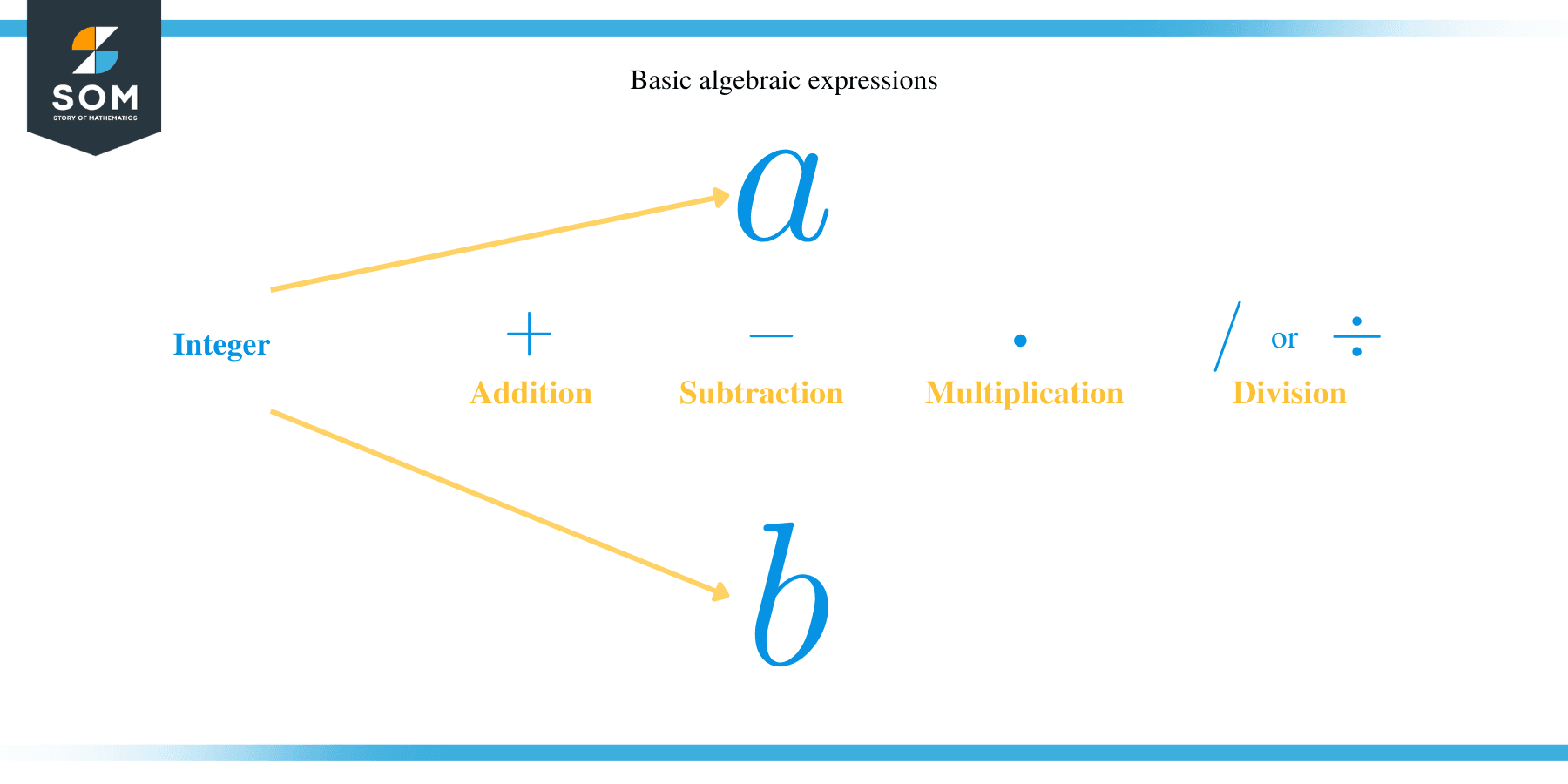
If a and b are two integers, the following are basic algebraic expressions:

• Addition equation: a + b
• Subtraction equation: b – a
• Multiplication equation: ab
• Division equation: a/b or a ÷ b

Basic algebra problems

The basic algebraic formulas are:

• a²– b² = (a – b) (a + b)
• (a + b)²= a² + 2ab + b²
• a²+ b² = (a – b)² + 2ab
• (a – b)²= a² – 2ab + b²
• (a + b + c)²= a² + b² + c² + 2ab + 2ac + 2bc
• (a – b – c)²= a² + b² + c² – 2ab – 2ac + 2bc
• (a + b)³= a³ + 3a²b + 3ab² + b³
• (a – b)³= a³ – 3a²b + 3ab² – b³

Example 1

Find the value of t, if t + 15 = 30

Solution

t = 30 – 15

t = 15

Example 2

Find the value of y, when, 9y = 63

Solution

Divide both sides by 9;

y = 63/9

y = 7

Example 3

If 21= b/7, find b:

Solution

Cross multiply:

b = 21 x 7

b = 147

Example 4

Consider a case of calculating grocery expense:

You want to go out shopping to buy 2 dozen eggs at $10, 3 loaves of bread each at $5, and 5 bottles of drinks, each at $8.  How much money do you need?

Solution

You can start solving this problem by assigning commodity a letter for instance:

Let dozens of eggs = a;

Breads= b;

Drinks =d

Price of a dozen= a = $10

Price of one bread=b = $5

Price of one bottle drinks=d= $8

=> Total expenditure= d + 3b + 5d

Substitute the values:

= $10 + 3($5) + 5($8) = $10 + $15 + $40 = $65

Therefore, the total expenditure is $65.