- Home
- >
- Complex Numbers – Properties, Graph, and Examples
JUMP TO TOPIC
Complex Numbers – Properties, Graph, and Examples
 You may have encountered numbers that are said to be imaginary. You may have been asked to disregard the square root of a negative number in the past, but we’ll focus on these types of complex numbers in this article. Along with the rest of the real numbers, these are part of a larger group of complex numbers.
You may have encountered numbers that are said to be imaginary. You may have been asked to disregard the square root of a negative number in the past, but we’ll focus on these types of complex numbers in this article. Along with the rest of the real numbers, these are part of a larger group of complex numbers.
Complex numbers are numbers that may contain real and imaginary parts.
This article is comprehensive of everything that we need to know when it comes to complex numbers, including:
- The parts that make up complex numbers.
- Properties and operation rules for complex numbers.
- What the form $a + bi$ represents in a complex plane.
Since complex numbers encompass an extensive range of numbers and are crucial elements in higher math, we must familiarize ourselves with all of the concepts mentioned. Why don’t we begin with the most fundamental of them all – the definition of complex numbers?
What is a complex number?
A complex number is a number that belongs to either the imaginary or real number groups. In short, they encompass all numbers belonging to the two mentioned groups. The general form of a complex number is $z = a + bi$, where $i$ represents $\sqrt{-1}$.
Let’s inspect the form that we’re given to understand the two crucial parts: real and imaginary.
$ \begin{aligned} \text{Complex Number } &= {\color{red} \boldsymbol{a}} + {\color{blue} \boldsymbol{bi}}\\ {\color{red} \boldsymbol{a}} &: \text{real number part}\\ {\color{blue} \boldsymbol{bi}} &: \text{imaginary number part}\end{aligned}$
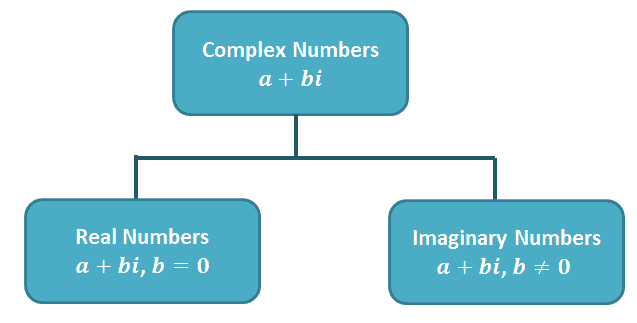
This chart can help you visualize the group of numbers that belong to the entire complex number system.
- Real numbers such as $4$, $\sqrt{5}$, $\dfrac{4}{2}$, and $\pi$ all belong to the complex number group as well.
- Imaginary numbers such as $\sqrt{-2}$, $-3 + 2i$, and $5 + 2\sqrt{-6}$ also belong under the complex number system group.
As long as the number can be expressed in the form $a + bi$, it’s considered part of the complex number group.
- For example, $4$ can be expressed as $4 + 0i$, showing that $4$ can be considered a complex number.
- Similarly, $\dfrac{2}{3}$ can be rewritten as $\dfrac{2}{3} + 0i$.
- Meanwhile, $4i $ can be written as $0 + 4i$, further confirming that imaginary numbers like $4i$ are part of the complex number group.
Notice how $i$ is often used to represent complex numbers? Let’s go ahead and review what we know about $i$ – an essential component of imaginary numbers.
Understanding the Imaginary Unit, $\boldsymbol{i}$
The number $i$ represents $\sqrt{-1}$ and consequently, $i^2 = -1$. We normally use $i$ to represent the square root of a negative number.
This also means that we can rewrite $\sqrt{-36}$ in terms of $i$.
- We can factor out $-1$ inside the square root and evaluate $\sqrt{36}$.
- Rewrite $\sqrt{-1}$ as $i$.
$ \begin{aligned}\sqrt{-36}&= \sqrt{36 \cdot -1}\\&=\sqrt{36} \cdot \sqrt{-1}\\&=6 \cdot i\\&= 6i\end{aligned}$
We have another important property to keep in mind when dealing with complex numbers: complex numbers equality.
Equality Property
The equality property will still apply for complex numbers: $a + bi = m + ni$ only when $a = m$ and $b = n$. What does this mean? Two complex numbers are equal if and only if the real parts are equal and the imaginary part is equal.
Now that we have thoroughly discussed the definition of complex numbers let’s go ahead and dive into how the rules of operations may differ or may be alike with the rules we have for real numbers.
How to solve complex numbers?
It’s helpful to think of complex numbers, $z = a + bi$, as binomials when we need to perform arithmetic operations. We consider the real number and imaginary parts as two separate variables. Here are some articles we’ve prepared for a much deeper discussion of the following topics.
- An introduction to adding complex numbers can be found here.
- Learn more about subtracting complex numbers
- Try out more complex examples of multiplying complex numbers here.
- Learn more about dividing complex numbers here.
Complex number rules
We can start by reviewing how to add and subtract complex numbers – again, and it helps to treat the two parts of the complex numbers as two different variables.
Adding and Subtracting Complex Numbers
When given two complex numbers, we can find their sum or difference by combining the real numbers and the imaginary numbers then simplifying the result.
- $(a + bi) + (m + ni) = (a + m) + (b + n)i$
- This means that to add two complex numbers, we add the two real parts and do the same for the imaginary parts.
- $(a + bi) – (m + ni) = (a – m) + (b – n)i$
- Similarly, if we want to subtract two complex numbers, we can subtract the real parts and combine them with the difference between the two imaginary parts.
Let’s go ahead and try finding the sum and difference of the two complex numbers, $(-3 + 5i)$ and $(4 – 2i)$.
- Remove the parenthesis and double-check the signs, especially when finding the difference between the two complex numbers.
- Group the real and imaginary number parts and combine each pair of terms.
| Sum | Difference |
| $\begin{aligned}(-3 + 5i) + (4 – 2i)&= -3 + 5i+ 4 – 2i\\&= -3 + 4 + 5i -2i\\&= (-3 + 4) + (5 – 2)i\\&= 1 + 3i\end{aligned}$ | $\begin{aligned}(-3 + 5i) – (4 – 2i)&= -3 + 5i- 4 + 2i\\&= -3 – 4 + 5i + 2i\\&= (-3 -4) + (5 + 2)i\\&= -7 + 7i\end{aligned}$ |
Multiplying Complex Numbers
If one of the complex numbers we want to multiply contains a single term, we can distribute this into the remaining complex number.
Let’s say we want to multiply $6i$ and $(2 – i)$. We distribute $6i$ into each of the terms inside the parenthesis. Keep in mind that $i^2 = -1$, so make sure to replace $i^2$ with $-1$ whenever possible.
$\begin{aligned}6i(2 – i)&= (6i)(2) – (6i)(i)\\&=12i – 6i^2\\&= 12i -6(-1)\\&=12i + 6\end{aligned}$
We use the FOIL method when we want to distribute two binomials, so we also apply the same process if we want to multiply two complex numbers of the form $(a+ bi)$ and $(m + ni)$.
Let’s review the FOIL method to multiply the two complex numbers, $(2 – 3i)$ and $(2 + 5i)$. We multiply the first terms, the terms outside and inside the parentheses, and the last term of each binomial.
$ \begin{aligned}(2 – 3i)(2 + 5i)\\\text{First} = 2 \cdot 2 \phantom{xx}\\\text{Outside} = 2 \cdot 5i \phantom{x}\\\text{Inside} = -3i \cdot 2 \\\text{Last} = -3i \cdot 5i \end{aligned}$
Combine these four terms to find the product of two complex numbers.
$ \begin{aligned}(2 – 3i)(2 + 5i) &= 4 + 10i- 6i – 15i^2\\&= 4 + 10i – 6i – 15(-1)\\&=4 + 10i – 6i + 15\\&= (4 + 15) + (10 – 6)i\\&= 19+ 4i \end{aligned}$
In general, the product of $(a+ bi)$ and $(m + ni)$ is equal to $(am –bn)(an + bm)i$.
Conjugates of Complex Numbers
We’ve learned about conjugates in the past, so if you need a quick refresher, make sure to check out this article we wrote about conjugates in math.
This means that the conjugate of $a + bi$ will be equal to $a – bi$. Here’s another interesting part – why don’t we multiply the two conjugates?
$ \begin{aligned}(a – bi)(a + bi)&= (a \cdot a – b \cdot b) + (a \cdot b – b \cdot a)i\\&=(a^2 + b^2) + 0i \\&= a^2 + b^2\end{aligned}$
This means that the product of a complex number and its conjugate is equal to the sum of the squares of their imaginary and real parts.
Dividing Complex Numbers
When we divide two complex numbers, we might end up with a denominator having an imaginary part. When this happens, we’ll apply a similar process when we want to rationalize a radical expression.
Let’s say we want to divide $(a + bi)$ by $(m +ni)$, we’ll end up with a quotient of $\dfrac{a + bi}{m + ni}$. If we want to eliminate the imaginary number found in the denominator, we can:
- Multiply both the numerator and denominator by $m – ni$.
- Simplify the numerator using the FOIL method.
- Simplify the numerator given that the product of a complex number and its conjugate is equal to the sum of the square of their real and imaginary parts.
$ \begin{aligned}\dfrac{a + bi}{m + ni}&= \dfrac{a + bi}{m + ni} \cdot \dfrac{\color{blue} m – ni}{\color{blue} m – ni}\\&= \dfrac{(a + bi){\color{blue}( m – ni)}}{(m + ni){\color{blue}( m – ni)}}\\&= \dfrac{(am -bn)+(mb -an)i}{(m +ni)(m -ni)}, \color{green}\text{FOIL method}\\&= \dfrac{(am -bn)+(mb -an)i}{m^2 + n^2}, \color{green}(a-bi)(a +bi) = a^2 + b^2\\&= \left( \dfrac{am – bn}{m^2 + n^2}\right )+ \left( \dfrac{mb – an}{m^2 + n^2}\right )i \end{aligned}$
This shows the general form of two complex numbers’ quotient, where $m + ni \neq 0$. We can apply similar steps when finding the quotient of other pairs of complex numbers.
We may need to use three or more of these rules for some problems, so make sure to review all these rules and check out the links we’ve provided earlier in this section.
Solving equations that involve complex numbers
Complex numbers can appear in equations. When this happens, it will be helpful to make use of the equality property whenever possible.
Keep in mind that we can only equate the real numbers part and the imaginary number parts based on the equality property.
Let’s try to solve for $x$ and $y$ in the equation, $5x – (2y + 3)i = 18 – 12i$.
Through the equality property, the real and imaginary parts must be equal to each other for the equation to be true.
| Equation | Real Part | Imaginary Part |
| $5x – (2y + 3)i$ | $5x$ | $-(2y + 3)$ |
| $18 – 12i$ | $18$ | $-2$ |
Let’s equate the real parts to solve for $x$:
$ \begin{aligned} 5x &= 18\\ x&= \dfrac{18}{5}\end{aligned}$
We do the same for the imaginary parts so we can solve for $y$:
$ \begin{aligned} -(2y + 3)&= -2\\ 2y + 3 &= 2\\2y &=-1\\y&= -\dfrac{1}{2}\end{aligned}$
Hence, we have $ x = \dfrac{18}{5}$ and $y = -\dfrac{1}{2}$.
How to graph complex numbers?
Now that we’ve learned about complex numbers and how we can manipulate their expressions let’s learn how to represent complex numbers on a graph.
When we talk about graphing complex numbers, it’s equally important for us to review what we know about complex planes.
Graphing Complex Numbers in Complex Planes
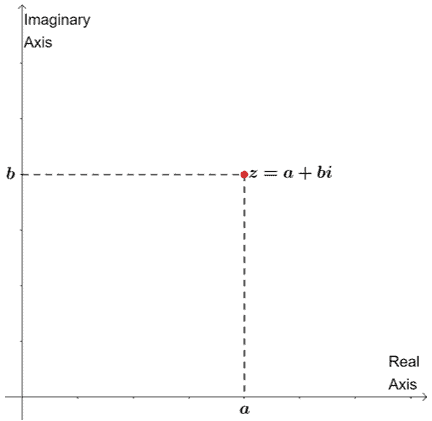
The complex plane is a coordinate system where the horizontal coordinate represents the real numbers. The vertical coordinates represent the imaginary parts.
This is also why the horizontal and vertical axes are called the real axis and imaginary axis.
Comparing this with our regular coordinate system, we can write the coordinate of $a + bi$ as $(x, y)$. This means that the way we plot the complex number will be similar.
- We’ll plot the point by moving $a$ units to the right if it’s positive or $a$ units to the left when it’s negative.
- Then we also move $b$ upward when it’s positive or downwards when it’s negative.
Here are some complex numbers graphed in one complex planes as examples:
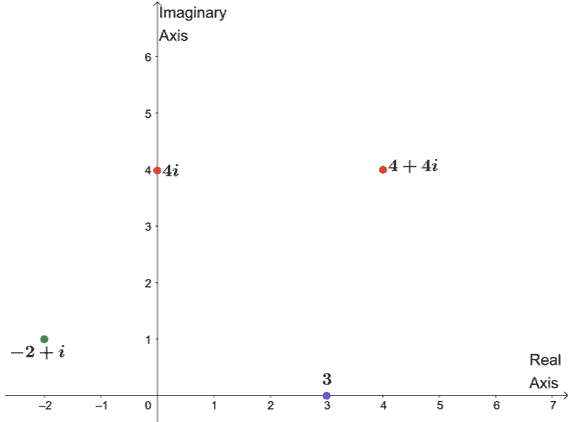
Let’s check each of the complex numbers graphed:
- $4 + 4i$: Graph the point $(4, 4)$ or a point that is $4$ units to the right and upward.
- $-2 + i$: Similarly, we can graph $(-2, 1)$ or plotting a point that’s $2$ to the left from the origin and one unit upward.
- $3$: Recall that $3 = 3 + 0i$, so that’s $(3, 0)$ or $3$ units along the real axis.
- $4i$: We can rewrite $4i$ as $0 + 4i$, so that’s $(0, 4)$. The point is expected to lie $4$ along the positive imaginary axis.
Understanding Absolute Values of $\boldsymbol{a + bi}$
The absolute value of a complex number represents the distance of the complex number from $0$. We use Pythagorean theorem ($c^2 = a^2 + b^2$, remember?) to derive the formula for the $a + bi$’s absolute value.
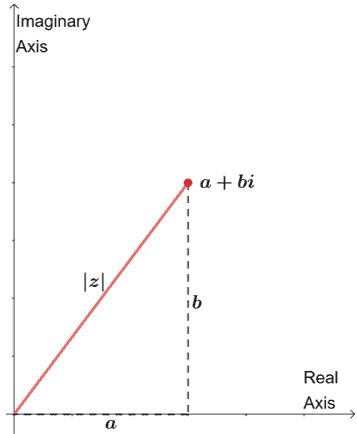
The graph above shows the absolute value of the complex number, $|z|$, by constructing a right triangle on the complex plane.
Using the Pythagorean theorem, we have $|z| = \sqrt{a^2 | b^2}$. This applies to all complex numbers as well.
Summary of complex numbers definition and properties
We’ll learn about complex numbers and more properties involving them in the next articles. For now, we should wrap this up and summarize what we’ve learned so far about complex numbers.
- The general form of complex numbers is $a + bi$, where $a$ and $b$ represent the real and imaginary parts, respectively.
- The number $i$ represents $\sqrt{-1}$, so $i^2 = -1$.
- To solve equations that involve complex numbers, always go back to the equality property.
- To graph $a + bi$ on a complex plane, we move $a$ units horizontally and $b$ units vertically.
Here’s a summary of the operations that can be done on two complex numbers, $a + bi$ and $m + ni$.
| Addition | $(a + bi) + (m + ni) = (a + m) + (b + n)i$ |
| Subtraction | $(a + bi) – (m + ni) = (a – m) + (b – n)i$ |
| Multiplication | $(a + bi) \cdot (m + ni) = (am – bn) + (bm + an)i$ |
| Division | $ \dfrac{a + bi}{m + ni} = \left( \dfrac{am – bn}{m^2 + n^2}\right )+ \left( \dfrac{mb – an}{m^2 + n^2}\right )i$ |
| Product of Two Conjugates | $(a + bi)(a – bi) = a^2 – b^2$ |
| Absolute Value | $|a + bi| = \sqrt{a^2 + b^2}$ |
Example 1
Simplify $(2 – 4i)(3 + i) – (2 – 3i)^2$.
Solution
Before we can simplify the expression, we’ll have to expand each group of binomials first:
- Applying the FOIL method on the first pair of binomials.
- Apply the perfect square trinomial property, (a – b)^2 = a^2 -2ab + b^2, to expand the last binomial.
$\begin{aligned} (2 – 4i)(3 + i) – (2 – 3i)^2 &= [(2\cdot 3 + 4\cdot1) -(-4 \cdot 3 + 2 \cdot 1)i] – (2 – 3i)^2\\&=(10 +12 i) – (2 – 3i)^2\\&= (10 + 12i) -[2^2 – 2 \cdot 3i + (3i)^2]\\&=(10 + 12i)- (4 -6i – 9) \end{aligned}$
Combine the real and imaginary parts to simplify the expression further.
$\begin{aligned} (10 + 12i)- (4 -6i – 9) &= 10 + 12i – 4 + 6i + 9\\&= (10 – 4 + 6) + (12 + 6)i\\&=12 + 18i \end{aligned}$
Hence, we have $(2 – 4i)(3 + i) – (2 – 3ui)^2 = 12 + 18i$.
Example 2
Simplify $\dfrac{(2 – i)^3}{(1 + i)^2}$.
Solution
What we can do is expand the numerator and denominator of the rational expression. Let’s begin by expanding $(2 – i)^3$ as shown below. Take note of the blue texts if you need a refresher on the property used in each step.
$\begin{aligned} (2-i)^3 &= (2- i)(2 -i)^2\\&= (2- i)[2^2 – 2(2)(i) +(i)^2], \phantom{xxx}\color{green} (a -b)^2 = a^2 -2ab + b^2\\&= (2 – i)[4 – 4i – 1], \phantom{xxxxxxxxxxx}\color{green} i^2 = -1\\&= (2 – i)(3 – 4i)\\&=(2\cdot3 – 4\cdot1) + [-1(3)+2(-4)]i, \color{green} \text{FOIL method}\\&= 2 – 11i\end{aligned}$
We can expand the denominator using the perfect square trinomial property as well.
$\begin{aligned} (1 + i)^2&= (1)^2 +2(1)(i) + (i)^2, \phantom{xx}\color{green} (a + b)^2 = a^2 + 2ab + b^2 \\&= 1 +- 2i – 1, \phantom{xxxxxxxxxxxxxx}\color{green} i^2 = -1\\&= 2i\end{aligned}$
Let’s replace the denominator and numerator with these simplified expressions and see what we have.
$ \begin{aligned} \dfrac{(2 – i)^3}{(1 + i)^2} &= \dfrac{2 – 11i}{2i}\end{aligned}$
To eliminate the imaginary part found in the denominator, we can multiply both denominator and numerator by $i$.
$ \begin{aligned} \dfrac{2 – 11i}{2i} \cdot \dfrac{\color{blue}i}{\color{blue}i}&= \dfrac{2{\color{blue}i} -(11i)({\color{blue}i})}{(2i)({\color{blue}i})}\\&=\dfrac{2i – 11i^2}{2i^2}\\&=\dfrac{2i + 11}{-2}\\&= \dfrac{2i}{-2}- \dfrac{11}{2}\\ &= -i- \dfrac{11}{2}\\&= -\dfrac{11}{2} -i\end{aligned}$
Hence, $\dfrac{(2 – i)^3}{(1 + i)^2} = -\dfrac{11}{2} -i $.
Example 3
Let’s observe the power of $i$ by filling in the table shown below.
| $\boldsymbol{i^1}$ | $\boldsymbol{i^5}$ | ||
| $\boldsymbol{i^2}$ | $\boldsymbol{i^6}$ | ||
| $\boldsymbol{i^3}$ | $\boldsymbol{i^7}$ | ||
| $\boldsymbol{i^4}$ | $\boldsymbol{i^8}$ |
a. What can you observe based on the two columns’ results?
b. Using your observation, find $i^k$ if the remainder of $k$ when it’s divided by $4$ is $2$?
c. Find the value of $i^{36} – i^{57}$.
Solution
We can start with {i} and multiply the current value with $i$. Use the fact that $i^2 = -1$ as well.
| $\boldsymbol{i^1}$ | $i^1 = i$ | $\boldsymbol{i^5}$ | $1 \cdot I = i$ |
| $\boldsymbol{i^2}$ | $i \cdot i = -1$ | $\boldsymbol{i^6}$ | $i \cdot i = -1$ |
| $\boldsymbol{i^3}$ | $-1 \cdot i = -i$ | $\boldsymbol{i^7}$ | $-1 \cdot i = -i$ |
| $\boldsymbol{i^4}$ | $-i \cdot i = -i^2 = 1$ | $\boldsymbol{i^8}$ | $-i \cdot i = -i^2 = 1$ |
The table above shows that values of $\{i, i^2, i^3, … i^8\}$. The two columns show the same result – meaning, the powers of i will return the same cycle of values shown for $i$, $i^2$, $i^3$, and $i^4$.
a. Let’s observe each pair that returns the same values:
- $i^5 = i^1 =1$: $5$ and $1$ return a remainder of $1$ when the powers are divided by $4$.
- $i^6 = i^2 =-1$: $6$ and $2$ return a remainder of $2$ when the powers are divided by $4$.
- $i^7 = i^3 =1$: $7$ and $3$ return a remainder of $3$ when the powers are divided by $4$.
- $i^8 = i^4 =1$: $8$ and $4$ are multiples of $4$ and will not return any remainder when the powers arty e divided by $4$.
How do we generalize this?
When $k$ is divided by $4$ and if the remainder is $1$, $2$ or $3$, $i^k$ will be equal to $i^1 = 1$, $i^2 = -1$, or $i^3 = -i$, respectively. If $k$ is a multiple of $4$, $i^k$ will be equal to $i^4 = 1$.
b. Apply what we’ve observed in a, since the remainder of $\dfrac{k}{4}$ is $2$, $i^k = i^2 = -1$.
We’ll apply our observations to find the values of $i^{36}$ and $i^{57}
- $36$ is a multiple of $4$, so $i^{36} = i^4 = 1$.
- $57$ returns a remainder of $1$ when divided by $4$, so $i^{57} = i^1 = i$.
c. Hence, $ i^{36} – i^{57} = 1 – i$.
Example 4
Simplify the expressions and solve for the unknown values.
a. $3 – 2i = x – (3 + i)$
b. $4 – 6i – x + 3yi = 8 – 3i$
c. $\dfrac{1}{y}= \dfrac{1}{2 + 5i}+ \dfrac{1}{5 – 2i}$
Solution
The first equation requires a straightforward approach of isolating $x$ on one side of the equation. We can add $(3 + i)$ on both sides of the equation.
$ \begin{aligned}3 – 2i&= x -(3 +i)\\3 -2i {\color{blue}+ (3 + i)}&= x- (3 + i){\color{blue}+ (3 + i)}\\6 – i &= x\\x&= 6 – i\end{aligned}$
a. Hence, we have $ x = 6 – i$.
Let’s isolate $x$ and $y$ on the left-hand side of the equation.
$\begin{aligned}4 – 6i – x + 3yi &= 8 – 3i\\ -x + 3yi &= 4 – 6i + 8 – 3i\\-x + 3yi &= (4 +8) + (-6-3)i\\-x + 3yi &= 12 + (-9)i\end{aligned}$
According to the equality property, for two complex numbers to be equal, the real number of parts must be equal to each other. The imaginary parts must be equal as well.
Let’s equate $-x$ with the real part on the right-hand side and equate $3y$ with the imaginary part of the right-hand side’s expression.
| $\begin{aligned}-x &= 12\\ x&=-12\end{aligned}$ | $\begin{aligned}3y &= -9\\y&= \dfrac{-9}{3}\\&=-3\end{aligned}$ |
b. This means that $x$ must be $-12$ and $y$ must be $-3$.
Let’s simplify the right-hand expression, $\dfrac{1}{2 + 5i}+ \dfrac{1}{5 – 2i}$, by rewriting each fraction so that they both share a common denominator, $(2 + 5i)(2 – 5i)$.
Observe that $ 5- 2i = -(2 + 5i)$, so $\dfrac{1}{2 + 5i}+ \dfrac{1}{5 – 2i} = \dfrac{1}{2 + 5i} – \dfrac{1}{2 – 5i}$.
$\begin{aligned}\dfrac{1}{2 + 5i} + \dfrac{1}{2 – 5i}&= \dfrac{1(2 – 5i)}{(2 + 5i)(2 – 5i)} + \dfrac{1(2 + 5i)}{(2 + 5i)(2 – 5i)}\\&= \dfrac{2 – 5i}{(2 + 5i)(2 – 5i)}+ \dfrac{2 + 5i}{(2 + 5i)(2 – 5i)}\\&=\dfrac{2 – 5i + 2 + 5i}{(2 + 5i)(2 – 5i)}\\&= \dfrac{4}{(2 + 5i)(2 – 5i)}\end{aligned}$
Simplify the denominator by using the conjugate properties of complex numbers, $(a – bi)(a + bi) = a^2 + b^2$.
$\begin{aligned}\dfrac{4}{(2 + 5i)(2 – 5i)} &= \dfrac{4}{(2)^2-(5i)^2}\\&= \dfrac{4}{4 – 25i^2}\\&= \dfrac{4}{4 – 25(-1)}\\&=\dfrac{4}{4 + 25}\\&= \dfrac{4}{29}\end{aligned}$
Let’s replace the equation’s right-hand expression to $\dfrac{4}{29}$ and solve for $y$.
$\begin{aligned}\dfrac{1}{y}&= \dfrac{4}{29}\\y&= \dfrac{29}{4}\end{aligned}$
c. This means that with enough manipulation on the complex expression, we could find $ y = \dfrac{24}{9}$.
Example 5
Graph the following complex numbers on a complex plane and indicate their corresponding absolute values or $|z|$.
a. $z = -2 + 3i$
b. $z = 6 – 12i$
c. $z = 6i$
d. $z = 12$
Solution
Let’s begin with $-2 + 3i$. Recall that the absolute value of the complex number, $z = a + bi$ can be determined using the property, $|z| = \sqrt{a^2 + b^2}$.
$ \begin{aligned}|z| &= \sqrt{(-2)^2 + (3)^2}\\&= \sqrt{4 + 9}\\&= \sqrt{13}\end{aligned}$
To graph $-2 + 3i$, let’s move $2$ units to the left and $3$ units upward.
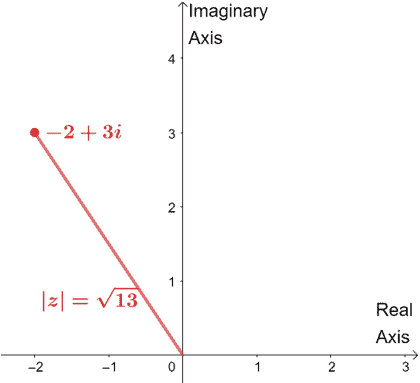
We’ll apply a similar process when graphing $6 – 12i$ and finding its absolute value.
$ \begin{aligned}|z| &= \sqrt{(6)^2 + (12)^2}\\&= \sqrt{36 + 144}\\&= \sqrt{180}\\&= \sqrt{36 \cdot 5}\\&= 6\sqrt{5}\end{aligned}$
The complex number is found $6$ units to the imaginary axis’s right and $12$ units up the real axis.
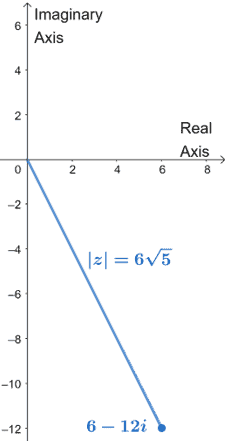
This graph shows the position of $6 – 12i$ on the complex plane and its absolute value, $|z|$.
The complex number, $6i$, only contains an imaginary part, so its position is expected to lie along the imaginary axis – in fact, $6$ units on the positive imaginary axis.
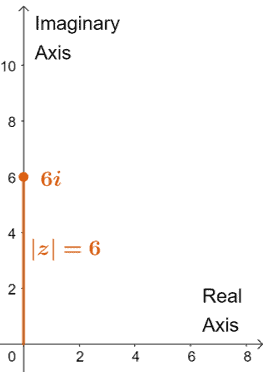
From inspection alone, we can see that the distance of $6i$ from the origin is $6$. We can also confirm this by using the formula for the absolute value.
Since $6i = 0 + 6i$, so we have:
$ \begin{aligned}|z| &= \sqrt{(6)^2 + (0)^2}\\&= \sqrt{36 + 0}\\&= \sqrt{36}\\&= 6\end{aligned}$
Working on the fourth number, we have $12 = 12+ 0i$. This means that we’re expecting the point lying along the real axis – $12$ units along the positive real axis.
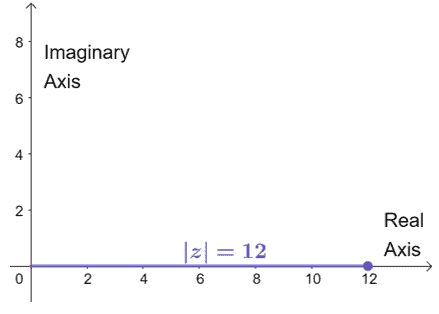
Similarly, we can see that the distance of the point from the origin is $12$ and can be confirmed by the traditional method of finding absolute values of complex numbers.
$ \begin{aligned}|z| &= \sqrt{(0)^2 + (12)^2}\\&= \sqrt{0 + 144}\\&= \sqrt{144}\\&= 12\end{aligned}$
Example 6
Given that $A$, $B$, $C$, and $D$ are four complex numbers graphed on one complex plane as shown below.
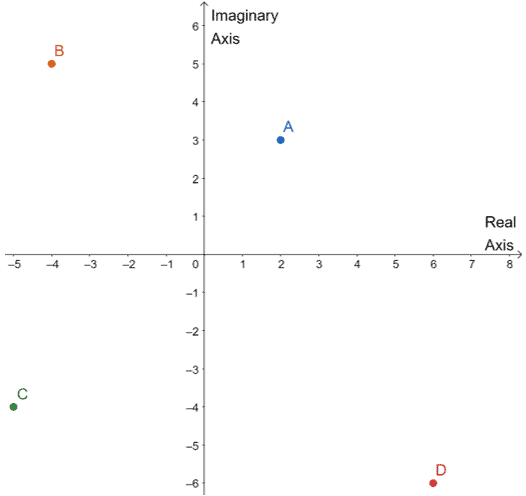
Find the values of the following:
a. $A + B$
b. $C – D$
c. $A \cdot C$
d. $\dfrac{B}{C}$
Solution
We can begin by finding what the four points represent. Take note of the distance of each point from the imaginary and real axes.
For example, $A$ is $2$ units from the right of the imaginary axis and $3$ units above the real axis. This means that $A$ = $(2, 3)$ = $2 + 3i$.
We’ll apply the same process for the remaining points and have the following result:
- $B = (-4, 5) = -4 + 5i$
- $C = (-5, -4) = -5 – 4i$
- $D = (6, -6) = 6 – 6i$
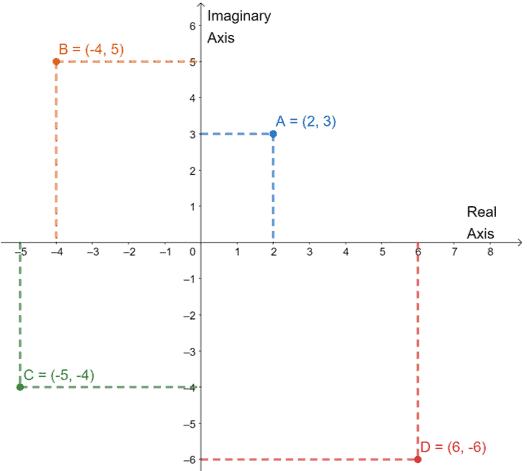
Let’s go ahead and find the sum of $A$ and $B$. Combine the real number parts and imaginary parts to add $(2 + 3i)$ and $(-4 + 5i)$.
$\begin{aligned}(2 + 3i) + (-4 + 5i)&= (2 + -4) + (3 + 5)i\\&=-2 + 8i\end{aligned}$
a. This means that $A + B = -2 + 8i$.
We’ll apply a similar process when finding the difference between $C$ and $D$.
$\begin{aligned}(-5 – 4i) – (6 – 6i)&= (-5 – 6) + (-4 – -6)i\\&=-11 + 2i\end{aligned}$
b. Hence, $C – D = -11 + 2i$.
To find the product of $A$ and $C$, we can apply the FOIL method as shown below.
$ \begin{aligned}(2 + 3i) \cdot (-5 – 4i) &= (2\cdot -5 -3 \cdot -4)+(3 \cdot -5 + 2 \cdot -4 )i\\&=(-10+12)+ (-15+-8)i\\&= 2 – 23i\end{aligned}$
c. This means that the product of $A$ and $C$ is $2 – 23i$.
The quotient of $B$ and $C$ is equal to $\dfrac{-4 + 5i}{-5 – 4i}$. Multiply both the numerator and denominator by the conjugate of $C$, which is $-5 + 4i$.
$\begin{aligned}\dfrac{-4 + 5i}{-5 – 4i}&= \dfrac{-4 + 5i}{-5 – 4i} \cdot \dfrac{\color{blue}-5 + 4i}{\color{blue}-5+ 4i}\\&= \dfrac{(-4 + 5i)({\color{blue}-5 + 4i})}{(-5 – 4i)({\color{blue}-5 + 4i})}\\&= \dfrac{(-4 + 5i)(-5 + 4i)}{(-5- 4i)(-5 + 4i)}\end{aligned}$
Apply the FOIL method on the numerator and the property of the conjugates’ product, $(a -bi)(a + bi) = a^2 + b^2$, to simplify the denominator.
$\begin{aligned} \dfrac{(-4 + 5i)(-5 + 4i)}{(-5- 4i)(-5 + 4i)}&= \dfrac{[-4(-5)-5(4)]+ [5(-5)+4(-4)]i}{(-5)^2 + (4)^2}\\&= \dfrac{(20 – 20) + (-25 – 16)i}{25 + 16}\\&= \dfrac{-41i}{41}\\&= -i\end{aligned}$
d. This means that $\dfrac{B}{C} = -i$.
Example 7
Given that $z = a + bi$, show that there is no value for $a$ and $b$ so that it satisfies $|z| – z = i$.
Solution
Let’s rewrite $|z|$ and $z$ in terms of $a$ and $b$. Hence, we have the following:
- $|z| = \sqrt{a^2 + b^2}$
- $z = a + bi$
$ \begin{aligned} |z| – z &= i \\ \sqrt{a^2 + b^2} – (a + bi)&= i\end{aligned}$
Group the real parts and imaginary parts on each side of the equation.
$\begin{aligned}(\sqrt{a^2 + b^2} – a) – b i = 0 + i \end{aligned}$
For the equation to be true, $\sqrt{a^2 + b^2} – a = 0$ and $-b = 1$.
This means that $b = -1$, so substitute this value into the first equation and find the value of $a$.
$\begin{aligned}\sqrt{a^2 + b^2} – a &=0 \\ \sqrt{a^2 + (-1)^2} – a &=0 \\\sqrt{a^2 + 1} -a&=0\\ \sqrt{a^2 + 1}&=a\\(\sqrt{a^2 + 1})^2 &= a^2\\a^2 + 1 &= a^2 \\1&=0 \Rightarrow \color{red}\text{No solution}\end{aligned}$
This shows that when $ b = -1$, the second equation will have no solution. This shows that it will be impossible for the system of equation, $\begin{matrix}\sqrt{a^2 + b^2} – a = 0 \\ b =- 1 \end{matrix}$.
Consequently, it’s impossible for a complex number that satisfies the equation $|z| – z = i$.
Practice Questions
![]()
Open Problem
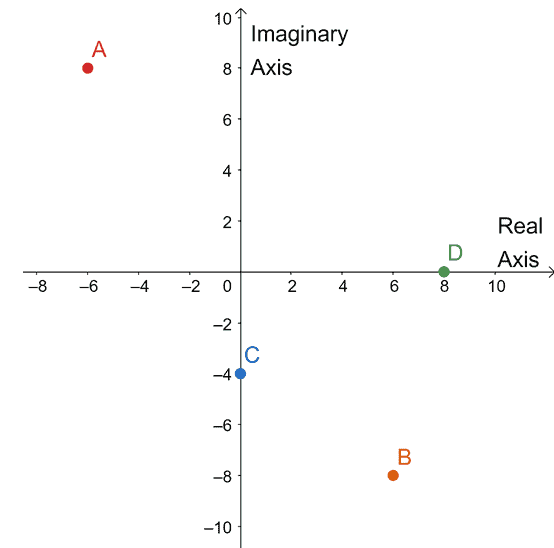
Graph the following complex numbers on a complex plane and indicate their corresponding absolute values or $|z|$.
a. $z = -6+ 8i$
b. $z = 6 – 8i$
c. $z = -4i$
d. $z = 8$
Open Problem Solution
Images/mathematical drawings are created with GeoGebra.
