Complex Rational Expressions – Definition, Methods, and Examples

We’ve worked extensively with complex and real numbers, but what if we need to manipulate these numbers as rational expressions within another rational expression? These expressions are known as complex rational expressions.

Complex rational expressions are expressions that contain rational fractions in either its numerator, denominator, or even both.

This article will show you how to manipulate complex expressions – from simple algebraic expressions to manipulating rational expressions containing complex numbers.

This means that we’ll utilize different algebraic tools – from expanding binomials to simplifying complex numbers in rational expressions.

This means that we’ll refresh different concepts throughout the article, so make sure to check out the links we’ll include in the discussions in case you need a quick refresher. For now, let’s go ahead and learn about the different types of complex rational expressions.

What is a complex rational expression?

As we have mentioned in the previous section, complex rational expressions contain a broad group of rational expressions that contain rational expressions in either its numerator or denominator. At times, they have rational expressions on both.

$ \dfrac{1}{\dfrac{1}{x} – \dfrac{1}{y}}$, $ \dfrac{\dfrac{1}{a – bi}}{m + ni}$, $ \dfrac{\dfrac{1}{\sqrt{2}x}}{\dfrac{2}{a – bi}}$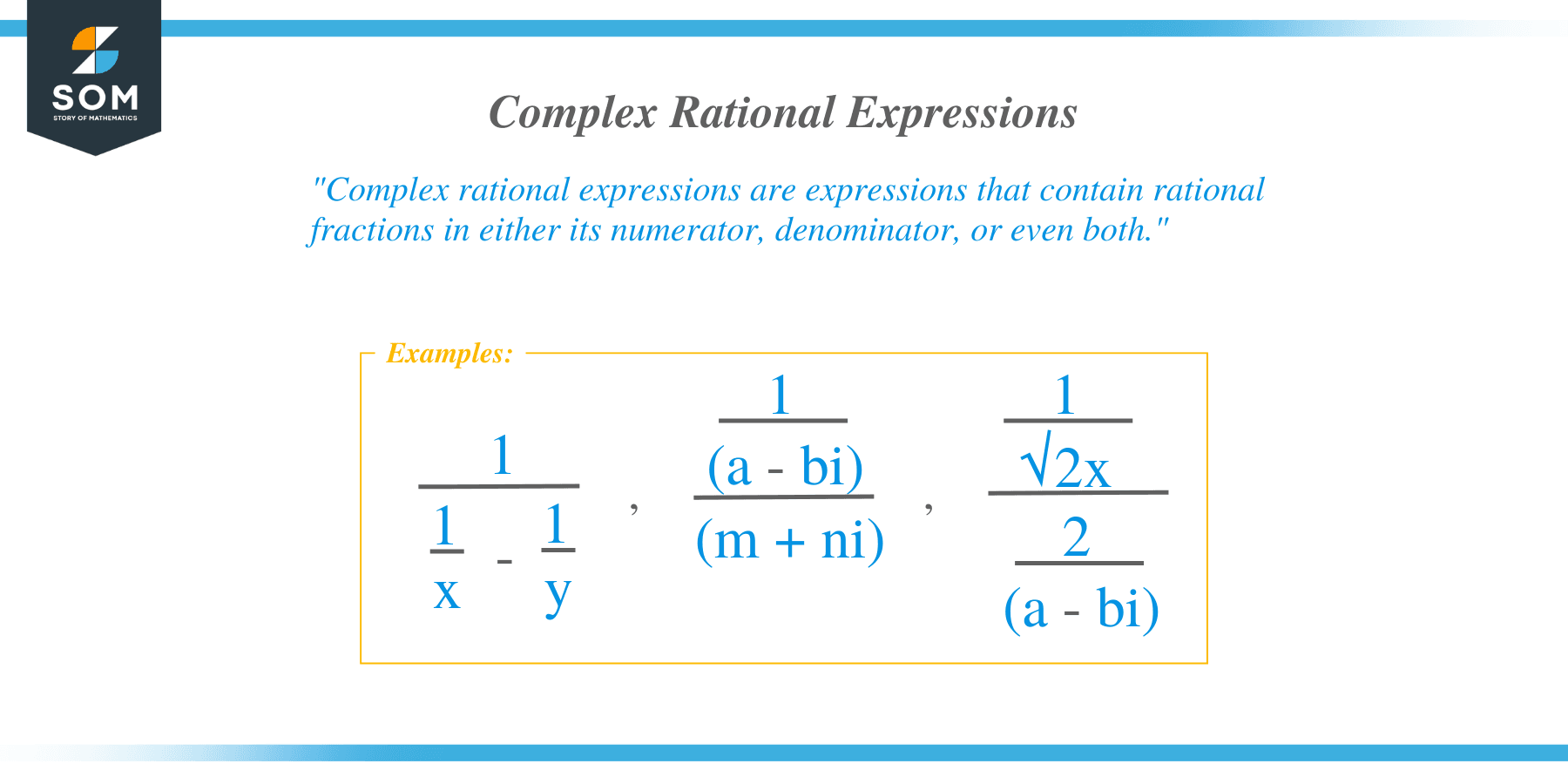    

In short, these complex rational expressions are like complex fractions, but this time, they may contain variables and different algebraic expressions.

As shown by the three examples above, complex rational expressions can also have radical expressions and complex numbers. Anything can be utilized – as long as they meet the conditions of complex rational expressions.

How to simplify complex rational expressions?

Since there is a wide range of complex rational expressions, the best technique we can use may vary. But we’ll summarize two methods that are generally used when simplifying complex rational expressions.

Method 1: Simplifying the Numerator and Denominator

This method simplifies the numerator and denominator individually before we simplify the complex expression and further.

1. Simplify the numerator and denominator so that it only contains one rational expression.
2. Divide the rational expressions found in the numerator by the denominator.
3. Simplify the result and rationalize the expressions whenever necessary.

Since we’ve just learned about complex numbers, why don’t we apply this method to simplify a complex expression involving complex numbers as well?

Let’s say we want to simplify $\dfrac{\dfrac{4 – 2i}{3} + \dfrac{2 – 3i}{5}}{\dfrac{1}{2 – 3i}}$.

Checking the numerator and the denominator, we can see that the numerator needs to be simplified while the denominator is already a simplified rational expression.

Let’s add the two rational expressions in the numerator first and simplify by adding the complex numbers.

$ \begin{aligned}\dfrac{4 – 2i}{3} + \dfrac{2 – 3i}{5} &= \dfrac{5(4 – 2i)}{15} + \dfrac{3(2 – 3i)}{15}\\&=\dfrac{20 – 10i}{15} + \dfrac{6 – 9i}{15}\\&= \dfrac{20 – 10i + 6 – 9i}{15}\\&= \dfrac{(20 + 6) + (-10-9)i}{15}\\&=\dfrac{26 – 19i}{15}\end{aligned}$

Replace the complex rational expression’s numerator with the simplified sum.

$\begin{aligned}\dfrac{\dfrac{4 – 2i}{3} + \dfrac{2 – 3i}{5}}{\dfrac{1}{2 – 3i}} &= \dfrac{\dfrac{26 – 19i}{15}}{\dfrac{1}{2 – 3i}} \end{aligned}$

Now, divide the numerator by the denominator to simplify the expression further.

$\begin{aligned}\dfrac{\dfrac{26 – 19i}{15}}{\dfrac{1}{2 – 3i}} &=\dfrac{26 – 19i}{15} \cdot \dfrac{2 – 3i}{1} \\&= \dfrac{(26 – 19i)(2 – 3i)}{15}  \end{aligned}$

We can simplify the resulting quotient by multiplying the complex numbers found in the quotient’s numerator.

$\begin{aligned}\dfrac{(26 – 19i)(2 – 3i)}{15} &= \dfrac{[26(2) + (-19i)(-3i)] + [-19(2) + 26(-3)]i}{15} \\&= \dfrac{(52 – 57) + (-38 – 78)i}{15}\\&=\dfrac{-5 – 116i}{15}\end{aligned}$

This means that we can have $\dfrac{\dfrac{4 – 2i}{3} + \dfrac{2 – 3i}{5}}{\dfrac{1}{2 – 3i}} = \dfrac{-5 – 116i}{15}$.

Method 2: Using the LCD of the fractions

Another way to simplify rational expressions is by multiplying both the main numerator and denominator by the LCD shared by the rational parts.

1. Identify the rational parts found in the complex expression’s numerator and denominator.
2. Find the LCD shared by these fraction parts and multiply the complex rational expression’s numerator and denominator by this LCD.
3. Simplify the result and rationalize the expressions whenever necessary.

We can also use the least common denominator or LCD of the rational parts that the complex rational expression has.

For example, if we want to simplify $ \dfrac{\dfrac{4}{2 – i}}{\dfrac{1}{2i} – \dfrac{3}{6i}}$, we can first find the LCD of the three rational part components: $\dfrac{4}{2 – i}$, $ \dfrac{1}{2i}$, and $ \dfrac{5}{6i}$.

Hence, multiply the complex rational expression’s numerator and denominator by $6i(2- i)$.

$\begin{aligned}\dfrac{\dfrac{4}{2 – i}}{\dfrac{1}{2i} – \dfrac{5}{6i}}  \cdot \dfrac{\color{blue}6i(2- i)}{\color{blue}6i(2- i)}&= \dfrac{\dfrac{4}{2 – i} \cdot {\color{blue}6i(2- i)}}{\dfrac{1}{2i} – \dfrac{5}{6i} \cdot {\color{blue}6i(2- i)}}\\&= \dfrac{4(6i)}{3(2-i) + 5(2 – i)}\\&=\dfrac{24i}{8(2 – i)}\end{aligned}$

We can simplify the expression further by dividing both the quotient’s numerator and denominator by $8$. Eliminate the denominator’s imaginary number part by multiplying the numerator and the denominator by the conjugate, $2 + i$.

$ \begin{aligned}\dfrac{24i}{8(2 – i)} &= \dfrac{3i}{2 – i} \cdot \dfrac{\color{blue} 2 + i}{\color{blue} 2 + i}\\&= \dfrac{3i{\color{blue} (2 + i)}}{(2 – i){\color{blue} (2 + i)}}\\&= \dfrac{6i + 3i^2}{2^2 + 1^2}\\&= \dfrac{-3 + 6i}{5}\end{aligned}$

Hence, we’ve shown how we can simplify $ \dfrac{\dfrac{4}{2 – i}}{\dfrac{1}{2i} – \dfrac{3}{6i}}$ to $\dfrac{-3 + 6i}{5}$.

Either of the two methods discussed should return equivalent values. Choosing which of the two should be used depends on which of the two methods would be easier for the given complex rational expressions.

Let’s go ahead and summarize what we know so far about complex rational expressions before we try out more problems. Don’t forget to review your rational expression and complex number techniques!

Summary of complex expressions definition and techniques

Here are some helpful pointers to keep in mind when working with complex rational expressions.

• Complex rational expressions come in different forms, but as long as it contains smaller rational parts in either (or both) its numerator and denominator, they’re considered complex rational expressions.
• They can be simplified by simplifying the numerator and denominator of the complex rational expressions first.
• Another way is by multiplying both the complex rational expression’s numerator and denominator by the shared LCD of the smaller rational parts.

These are the general rules for simplifying and evaluating complex rational expressions. Of course, it’s important to apply previous algebraic techniques, so make sure to review the links we’ve included all over this article!

Example 1

If $\dfrac{3 – \dfrac{3}{x}}{9 – \dfrac{9}{x^2}} = \dfrac{Ax}{Bx + C}$, what are the values of $A$, $B$, and $C$?

Solution

Let’s go ahead and use the first technique to simplify the complex rational expression.

Simplify the numerator by finding the difference between $3$ and $\dfrac{3}{x}$ as well as $9$ and $\dfrac{9}{x^2}$.

Replace the rational expression’s numerator and denominator with their corresponding differences. We can then divide the two fraction parts and simplify the result.

$\begin{aligned} \dfrac{3 – \dfrac{3}{x}}{9 – \dfrac{9}{x^2}} &= \dfrac{\dfrac{3x – 3}{x}}{\dfrac{9x^2 – 9}{x^2}}\\&= \dfrac{3x – 3}{x} \cdot \dfrac{x^2}{9x^2 -9}\end{aligned}$

Simplify the expression further by cancelling out common factors shared by the numerator and denominator.

$\begin{aligned} \dfrac{3x – 3}{x} \cdot \dfrac{x^2}{9x^2 -9} &= \dfrac{3(x – 1)}{x} \cdot \dfrac{x^2}{9(x^2 – 1)}\\&=\dfrac{3\cancel{(x – 1)}}{\cancel{x}} \cdot \dfrac{\cancel{x }\cdot x}{9\cancel{(x- 1)}(x + 1)} \\ &= \dfrac{3x}{9(x + 1)}\\&= \dfrac{x}{3(x + 1)}\\&= \dfrac{x}{3x + 3}\end{aligned}$

Comparing the simplified form of $\dfrac{3 – \dfrac{3}{x}}{9 – \dfrac{9}{x^2}}$ to $\dfrac{Ax}{Bx +C}$, we have:

$\begin{aligned} \dfrac{x}{3x + 3} &= \dfrac{Ax}{Bx + c}\\\\A&=1\\B&=3\\C &= 3\end{aligned}$

This means that by simplifying the complex rational expression, we were able to determine the values of $A$, $B$, and $C$ as shown above.

Example 2

Simplify the complex rational expression, $\dfrac{\dfrac{2i}{x + 1} + \dfrac{4 – 2i}{x + 3}}{\dfrac{1}{x^2 + 4x + 3}}$.

Solution

Since $(x + 1)(x + 3) = x^2 + 4x + 3$, it’s best that we use the second technique to simplify the rational expression.

We can multiply the complex expression’s numerator and denominator by $(x + 1)(x + 3)$.

$\begin{aligned} \dfrac{\dfrac{2i}{x + 1} + \dfrac{4 – 2i}{x + 3}}{\dfrac{1}{x^2 + 4x + 3}}&= \dfrac{\dfrac{2i}{x + 1} + \dfrac{4 – 2i}{x + 3}}{\dfrac{1}{x^2 + 4x + 3}} \cdot \dfrac{\color{blue}(x + 1)(x + 3)}{\color{blue}(x + 1)(x + 3)} \\&= \dfrac{\dfrac{2i}{x+1} \cdot {\color{blue}(x+1)(x+3)} + \dfrac{3 – 2i}{x+3} \cdot {\color{blue}(x+1)(x+3)}}{\dfrac{1}{x^2 + 4x + 3} \cdot {\color{blue}(x+1)(x+3)}}\end{aligned}$

Let’s go ahead and simplify the numerator and denominator to simplify the resulting quotient.

$\begin{aligned} \dfrac{\dfrac{2i}{x+1} \cdot {\color{blue}(x+1)(x+3)} + \dfrac{3 – 2i}{x+3} \cdot {\color{blue}(x+1)(x+3)}}{\dfrac{1}{x^2 + 4x + 3} \cdot {\color{blue}(x+1)(x+3)}} &= \dfrac{2i(x + 3) + (3-2i)(x + 1)}{1}\\&= 2i(x + 3) + (3-2i)(x + 1)\\&= (2xi + 6i) + (3x + 3-2xi-2i)\end{aligned}$

Simplify the expression further by like terms, as shown below.

$\begin{aligned} (2xi + 6i) + (3x + 3-2xi-2i) &= (2i – 2i + 3)x + (6i -2i + 3)\\&=3x + 4i + 3\\&= (3x + 3) + 4i\end{aligned}$

This means that $\dfrac{\dfrac{2i}{x + 1} + \dfrac{4 – 2i}{x + 3}}{\dfrac{1}{x^2 + 4x + 3}}$ is equal to $(3x  +3) + 4i$ when simplified.

Example 3

Simplify the complex rational expression, $\dfrac{4x^{-1} + i5y^{-1}}{16x^{-2} + i25y^{-2}}$.

Solution

Recall that $a^{-n} = \dfrac{1}{a^n}$, so let’s rewrite the expression first using this exponential property.

$\begin{aligned} \dfrac{4x^{-1} + i5y^{-1}}{16x^{-2} + i25y^{-2}}&=\dfrac{\dfrac{1}{4x}+ \dfrac{1}{5y}i}{\dfrac{1}{16x^2}+ \dfrac{1}{25y^2}i}\end{aligned}$

We can then find the sum of the rational parts found in the numerator as well as the denominator separately first.

Take note that $i = \sqrt{-1}$ that’s why we can simply combine the terms in the numerator for each of the sum. Now, rewrite the numerator and denominator of the original complex expression using the results.

$\begin{aligned} \dfrac{4x^{-1} + i5y^{-1}}{16x^{-2} + i25y^{-2}} &= \dfrac{\dfrac{5y + i4x}{20xy}}{\dfrac{25y^2 + i16x^2}{400x^2y^2}}\end{aligned}$

Divide the two resulting fractions on the numerator and denominator.   Make sure to cancel out common factors.

$\begin{aligned} \dfrac{\dfrac{5y + i4x}{20xy}}{\dfrac{25y^2 + i16x^2}{400x^2y^2}} &=\dfrac{5y + i4x}{20xy} \cdot  \dfrac{400x^2y^2}{25y^2 + i16x^2} \\&= \dfrac{5y + i4x}{20xy} \cdot \dfrac{(20xy)(20xy)}{25y^2 + i16x^2}\\&= \dfrac{20xy(5y + i4x)}{25y^2 + i16x^2}\end{aligned}$

Eliminate the complex number in the denominator by multiplying the numerator and denominator by the conjugate of $25y^2 + i16x^2$.

$\begin{aligned} \dfrac{20xy(5y + i4x)}{25y^2 + i16x^2} \cdot \dfrac{\color{blue} 25y^2 – i16x^2}{\color{blue} 25y^2 – i16x^2}&= \dfrac{20xy(5y + i4x){\color{blue}(25y^2 – i16x^2)}}{(25y^2 + i16x^2){\color{blue}(25y^2 – i16x^2)}} \\&= \dfrac{20xy(5y + i4x)(25y^2 – i 16x^2)}{(25y^2)^2 + (16x^2)^2}\end{aligned}$

We can then expand the numerator and combine like terms to further simplify the result.

$\begin{aligned} \dfrac{20xy(5y + i4x)(25y^2 – i 16x^2)}{(25y^2)^2 + (16x^2)^2} &= \dfrac{20xy(125y^3 – i80x^2y – i100xy^2 – i^264x^3)}{625y^4 + 256x^4}\\&= \dfrac{20xy(125y^3 – i80x^2y – i100xy^2 + 64x^3)}{625y^4 + 256x^4}\\&= \dfrac{2500xy^4- i1600x^3y^2 – i2000x^2y^3 + 1280x^4y}{625y^4 + 256x^4}\end{aligned}$

This means that $\dfrac{4x^{-1} + i5y^{-1}}{16x^{-2} + i25y^{-2}}$ is equivalent to $\dfrac{2500xy^4- i1600x^3y^2 – i2000x^2y^3 + 1280x^4y}{625y^4 + 256x^4}$ when simplified.

We’ve applied several algebraic processes in this problem, so make sure to take a close look at each stage of the calculation to make sure you’ve caught up with all the techniques.