Continuous function – Conditions, Discontinuities, and Examples

Ever heard of a function being described as continuous in the past? These are the functions with graphs that do not contain holes, asymptotes, and gaps between curves. These “nice” graphs we’ve encountered in the past are called continuous functions.

Continuous functions are functions that look smooth throughout, and we can graph them without lifting our own pens.

We can also assess a function’s continuity through limits and higher maths – and that’s our focus in this article.

• We’ll learn about the conditions of continuous functions.
• We’ll apply our techniques in evaluating limits to confirm if a function is continuous.
• Apply graphical techniques as well to identify whether a graph is continuous or not.

In Calculus, we’ll also encounter continuous functions again, so learning about them now can be helpful, especially for those about to progress to differential calculus soon. Why don’t we go ahead and understand what these functions represent?

What is a continuous function?

Continuous functions are functions that have no restrictions throughout their domain or a given interval. Their graphs won’t contain any asymptotes or signs of discontinuities as well.

The graph of $f(x) = x^3 – 4x^2 – x + 10$ as shown below is a great example of a continuous function’s graph. As can be seen, the graph extends throughout both the $x$-axis’ positive and negative sides.

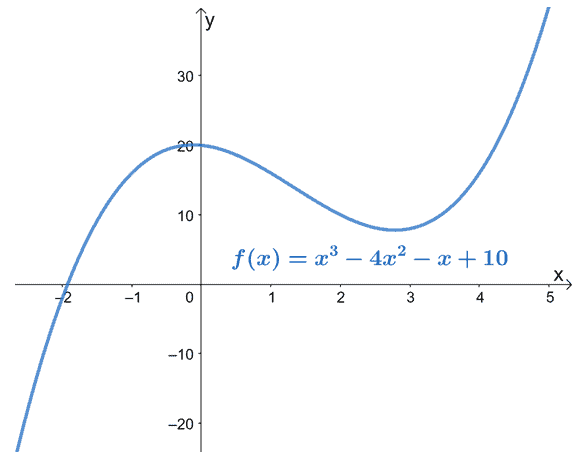
Fun fact: all polynomial functions are considered continuous throughout their domain since they have no restrictions on their domain.

We can define continuous functions based on their function’s properties as well. We’ll learn more about identifying continuous functions in the later section, and we’ll also learn how to identify functions that are not continuous.

How to determine if a function is continuous?

In this section, we’ll discuss the more formal conditions a function must satisfy before we can establish that it’s continuous throughout its domain or a given interval.

This will also help us in the process of confirming whether a given function is continuous or not.

Continuous function definition

A function is also continuous at $x = a$ when it satisfies all three conditions shown below:

• The function is defined at $a$ or in other words, $a$ is part of $f(x)$’s domain.
• The limit of the function as $x$ approaches $a$ must exist.
• Last, the value of $f(a)$ and $\lim_{x \rightarrow a} f(x)$ must be equal.

This definition will also guide us in identifying whether a function is continuous.

Remember we mentioned that all polynomial functions are continuous throughout their domain?

We can verify this by using the three conditions:

• Let’s say we have $P(x)$, a polynomial function, the value of $P(x)$ at $x = a$ is defined at $P(a)$.
• The limit for all polynomials at $x = a$ exist.
• From our previous discussion on limit laws and evaluating limits, we can show that $\lim_{x \rightarrow a} P(x) = P(a)$.

Let’s take a look at the graph of $f(x) = x^2 +1$, a polynomial function – quadratic function, to be exact.

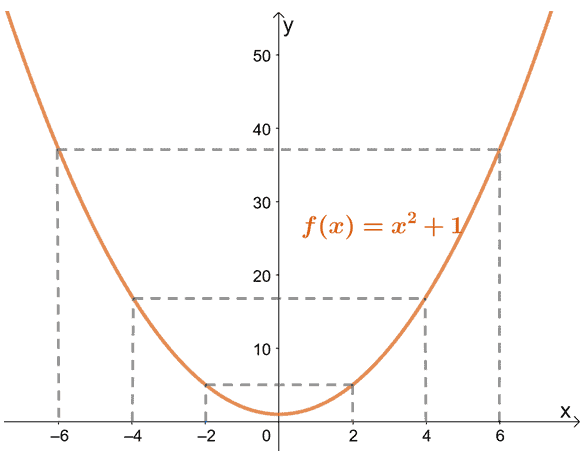
By inspection alone, we can see that at the points selected, the value of $f(x)$ will be equal to the limit of $f(x)$.

• For example, at $x = 2$ and $x = -2$, both values are defined and are part of the domain of $f(x)$.
• The limit of $f(x)$ as $x$ approaches either $-2$ or $2$ are defined as well from both ends.
• We can also see that $\lim_{x \rightarrow -2} f(x) = f(-2) = 5$ and $\lim_{x \rightarrow 2} f(x) = f(2) = 5$.

This also confirms what we know – $f(x)$ is continuous at $x =-2$ and $ x= -2$. We can also observe similar behavior at $x = \{-6, -4, 4, 6 \}$. In fact, throughout $x \in (-\infty, \infty)$, $f(x) = x^2 + 1$ will be continuous.

Now, what happens if the function at $x = a$ does not meet the three conditions? The next section will thoroughly discuss the discontinuities. We’ll also learn how we can identify functions that are, this time, not continuous and see how we can rewrite the function so that it becomes continuous.

Understanding discontinuity

When we want to understand continuity, it is also important for us to understand the circumstances and conditions when a given function is not continuous at $x = a$.

When this happens, we consider $x = a$ a discontinuity of a function.

There are three common reasons why a function may not be continuous at $x = a$: it either contains a hole, an asymptote, or an inconsistency at $x = a$.

Jump discontinuity

This discontinuity happens when the one-sided limits of the function as it approaches $a^{-}$ and $a^{+}$ are different.

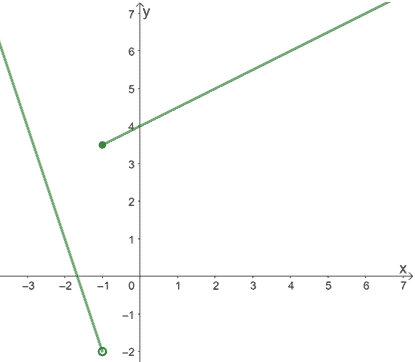
The graph above illustrates how a function may not be continuous because their one-sided limits at $x=a$ are not equal. See how as $x$ approaches $-1$ and $1$, the value of $f(x)$ “jumps”? Hence, its name.

For this graph’s case, we can see that as $x$ approaches from the left of $-1$, we have $\lim_{x \rightarrow -1^{-1}} f(x) = -2$ and $\lim_{x \rightarrow -1^{+1}} f(x) = 4$. From this, we can see that since the regular limit won’t exist, the second condition of continuous functions won’t apply.

Jump discontinuities are often found in piecewise functions, so always check the one-sided limits for these types of functions.

Removable discontinuity

This type of discontinuity is often found in rational functions – holes of rational functions are, in fact, considered removable discontinuities. Removable discontinuities occur when the function is not defined at $x = a$.

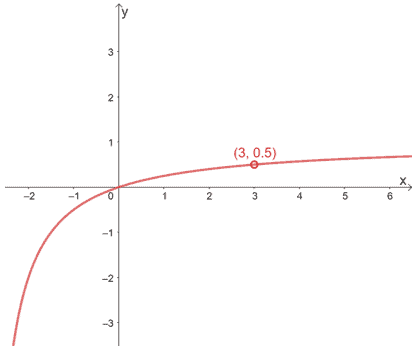
This graph here shows a removable discontinuity at $x = 3$. This means that the function is defined through the rest of its domain except when $x = 3$.

The limit of the function will be $3$ on both sides, so what condition is it not meeting so that it becomes continuous? It’s the first one: the function must be defined at $x = a$.

This graph is in fact, half of $f(x) = \dfrac{x^2 -3x}{x^2 – 9}$, and we can double check $f(x)$’s limit algebraically as shown below.

$\begin{aligned} \lim_{x \rightarrow 3}\dfrac{x^2 -3x}{x^2 – 9}&= \lim_{x \rightarrow 3}\dfrac{x(x – 3)}{(x – 3)(x + 3)}\\&= \lim_{x \rightarrow 3} \dfrac{x}{x + 3}\\&=\dfrac{1}{2}\end{aligned}$

What if we want to make this function continuous? We can instead redefine the function into a piecewise function and single out the hole.

$f(x)=\left\{\begin{matrix} \dfrac{x^2 -3x}{x^2 -9},&\text{where } x \neq 3\\ \dfrac{1}{2},&\text{where }x = 3\end{matrix}\right.$

We now have a continuous function after accounting for the hole!

Discontinuity from vertical asymptotes

When a function contains a vertical asymptote at $ x= a$, the function has a discontinuity at $x = a$ as well.

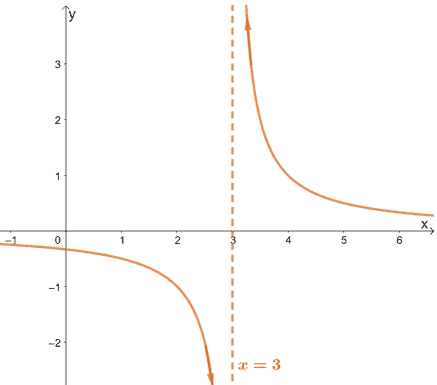
The graph above is an example of a function that is not continuous because of a discontinuity at $x = 3$. Observe how as $x$ approaches from the left of $3$, the function approaches $-\infty$? Similarly, when $x$ approaches from the right of $3$, the function approaches $\infty$.

This means that the function’s limit does not exist and consequently, making it not continuous. This is also why the other name for this discontinuity is infinite discontinuity.

Keep in mind that a function may contain more than one discontinuity, so better double-check your function’s graph or limits well.

Now that we’ve dealt with the possible conditions where a function may not be continuous, why don’t we go ahead and learn more of other important properties of continuous functions?

What are other important properties of continuous functions?

We’ve now learned about identifying continuous functions and being able to assess functions for discontinuities. These properties below will help us confirm and prove if a function is continuous by using simpler functions.

Property 1: $\boldsymbol{k \cdot f(x)}$

When $k$ is a constant and $f(x)$ is a continuous function when $x = a$, then $k\cdot f(x)$ is also continuous at $ x= a$.

Property 2: $\boldsymbol{f(x) + g(x)}$

When $f(x)$ and $g(x)$ are both continuous functions when $x = a$, then the resulting function when we add $f(x)$ and $g(x)$ will also be continuous at $x =a$.

Property 3: $\boldsymbol{f(x) – g(x)}$

When $f(x)$ and $g(x)$ are both continuous functions when $x = a$, then the difference between the functions will also be a function that is continuous when $x = a$.

Property 4: $\boldsymbol{f(x) \cdot g(x)}$

If the functions $f(x)$ and $g(x)$ are continuous functions at $x = a$, the two functions’ product is also continuous at $x = a$.

Property 5: $\boldsymbol{\dfrac{f(x)}{g(x)}}$

If the functions $f(x)$ and $g(x)$ are continuous when $x = a$ and $g(a) \neq 0$, the ratio of $f(x)$ and $g(x)$, is also continuous at $x = a$.

Property 6: $\boldsymbol{f(g(x))}$

When $g(x)$ is continuous at $x = a$ and $f(x)$ is continuous at $x = g(a)$, then $f(g(x))$ will also be continuous at $x = a$.

Common functions that are continuous

Here are some of the functions that you may have encountered in the past that are known to be continuous within their domain.

• Sine function: $y = \sin x$
• Cosine function: $y = \cos x$
• Tangent function: $y = \tan x$
• Radical function: $y = \sqrt{x}$
• Exponential function: $y = a^x$, where $a > 0$ and $y = e^x$
• Natural logarithmic function: $y = \ln x$

You might wonder, tangent and radical functions have restrictions, so how are they continuous? This is when it’s important to highlight that these functions are continuous only within their domain.

For example, $\sqrt{x – 1}$ has a domain of $[0, \infty)$, so it’s expected to be continuous within the interval, $[0, \infty)$. Meaning, if asked whether $\sqrt{x – 1}$ is continuous at $x = -2$, of course, it won’t be since the function is not defined at $x = -2$.

This can help you identify continuous functions (along with the properties discussed above), especially when it has complex expressions.

Let’s go ahead and try out more examples to understand continuous and discontinuous functions better.

Example 1

Fill in the blanks to make the following statements true.

a. If $f(2) = -24$ and $f(x)$ is a continuous function, $\lim_{x \rightarrow 2} f(x)$ is equal to ____________.
b. If $g(x)$ has a hole at $(5, 4)$, the function is not continuous at ____________.
c. If h(x) contains a vertical asymptote at $x = -1$, the function is not continuous when _________.

Solution

Recall that when the function and its limit are defined at $x = a$, the third condition will require the two’s values to be equal.

a. This means that for $f(x)$ to be continuous, $\lim_{x \rightarrow 2} f(x)$ must also be equal to $\boldsymbol{-24}$.
When a function has a hole at $(a, b)$, there is removable discontinuity at $x = a$.
b. Since $g(x)$ has a hole at $(5, 4)$, it has a removable discontinuity at the $x$-coordinate of the hole. Meaning, $g(x)$ is not continuous at $\boldsymbol{x = 5}$.
When a function contains a vertical asymptote, its value and limit will be undefined at the vertical asymptote’s value.
c. Using this information, $h(x)$ is continuous throughout its domain except it’s equal to $-1$. Hence, the function is continuous when $\boldsymbol{x = -1}$.

Example 2

Discuss the continuity of the following function at the given corresponding points.

a. $f(x) = -4x^2 + 8$, when $x = 4$
b. $g(x) = \dfrac{5x + 1}{2x – 3}$, when $x = 3$
c. $h(x) = \sqrt{x^2 + 2}$, when $x = -2$

Solution

When confirming whether a function is continuous, make sure to check three things:

1. The function is defined at $ x= a$.
2. The limit exists when the function approaches $a$.
3. Last, if we have $f(x)$, $\lim_{x \rightarrow a} f(x) = f(a)$.

Let’s start with $f(x) = -4x^2 + 8$ and see if this function satisfies all three conditions.

• Since $f(x)$ is a polynomial, all values of $x$, including $4$ is defined at $f(x)$. In fact, $f(4)$ is equal to $-4(4)^2 + 8 = -56$.
• For polynomial functions, $\lim_{x \rightarrow a} f(x) = f(a)$, so $\lim_{x \rightarrow 4} f(4) = -56$.
• This also means that $\lim_{x \rightarrow 4} f(x) = f(4)$.

As we have discussed in the previous sections, all polynomials are continuous.

a. All these confirm that $\boldsymbol{f(x)}$ is a continuous function.

 We can inspect the second function, $g(x) = \dfrac{5x + 1}{2x  – 3}$, using the same process. Let’s begin by evaluating $g(3)$ as shown below.

$\begin{aligned}g(3)&=\dfrac{5(3) + 1}{2(3)  – 3}\\&=\dfrac{16}{0}\end{aligned}$

From this, we can see that $g(3)$ is not defined. We don’t need to check the remaining conditions when this happens.

b. Since $g(3)$ is not defined, $\boldsymbol{g(x)}$ is not a continuous function.

Let’s move on to the third function – $ h(x) = \sqrt{x^2 + 2}$.

• Substitute $x = -2$ into the expression for $h(x)$. Hence, we have $ h(-2) = \sqrt{((-2)^2 + 2} = \sqrt{6}$. This means that $h(x)$ is defined at $x = -2$.
• Next, let’s evaluate the limit of $h(x)$ as it approaches $x = -2$: $\lim_{x \rightarrow -2} \sqrt{x^2 + 2} = \sqrt{(-2)^2 + 2} = \sqrt{6}$.
• Comparing the limit and value of the $h(x)$ when $x = -2$, we have $h(-2) = \lim_{x \rightarrow -2} h(x) = \sqrt{6}$.

c. Seeing that $h(x)$ satisfies all three conditions when $x = -2$, $\boldsymbol{h(x)}$ is a continuous function.

Example 3

Is the function, $ f(x)=\left\{\begin{matrix}-3x + 1,&x<4\\ 2x – 5,&x\geq4\end{matrix}\right.$, continuous at $x = 4$?

Solution

As we have done in the previous example, we can check for continuity by reviewing the three conditions.

Starting by checking if $f(a)$ is defined. When $x \geq 4$, we have $f(x)$ = 2x – 5. This means that $f(4) = 2(4) – 5 = 3$.

Let’s go ahead and observe the limit of $f(x)$ as it approaches $4$. We’re working with a piecewise function, so it’s best to check the one-sided limits of $f(x)$.

From this, we can see that $\lim_{x \rightarrow 4^{-}} f(x) \neq \lim_{x \rightarrow 4^{+}} f(x)$, so the limit for $f(x)$ is not defined.

At this point, since $f(x)$ does not meet the second condition, $f(x)$ is not continuous.

Example 4

Identify which of the following functions are discontinuous. If working with a discontinuous function, identify the type of discontinuity it has.

a. $f(x) = -2x^3 + 5x – 9$
b. $f(x) = \dfrac{1}{4x^2 + 4}$
c. $f(x) = \dfrac{2x^2 – 2x}{4x}$
d. $f(x) = \dfrac{x – 4}{x^2 – 6x + 8}$

Solution

a. Since the function, $f(x) = -2x^3 + 5x – 9$, is a polynomial function, it is continuous throughout its domain, $(-\infty, \infty)$.

Although the function is rational and may contain asymptotes, the denominator of $f(x)$ is $4x^2 + 4$, which can never be negative.

b. This means that $f(x) = \dfrac{1}{4x^2 + 4}$ has no restrictions and when this happens, this rational function is continuous.

For $f(x) = \dfrac{2x^2 – 2x}{4x}$, let’s factor the numerator first and see if the numerator and denominator share a common factor.

$\begin{aligned}\dfrac{2x^2 – 2x}{4x}&= \dfrac{2x(x – 2)}{2(2x)}\\&= \dfrac{\cancel{2x}(x – 2)}{2\cancel{(2x)}}\\&=\dfrac{x-2}{2}\end{aligned}$

Since $f(x)$’s numerator and denominator share a common factor of $2x$, so it has a hole at $x = 0$.

To find the hole’s $y$-coordinate, we can substitute $x = 0$ into the simplified form of $f(x)$.

$\begin{aligned}f(x) &= \dfrac{x-2}{2}\\ f(0)&= \dfrac{0-2}{2}\\&=-1\end{aligned}$

c. Since $f(x)$ has a hole and consequently, a discontinuity at $x = 0$. Since we have a discontinuity at a hole, $f(x)$ is not continuous and we can consider it a removable discontinuity.

Let’s go ahead and express the denominator of $f(x)$ in factored form: $\dfrac{x – 4}{x^2 – 6x + 8} = \dfrac{x – 4}{(x -2)(x – 4)}$.

Since $x – 4$ is a common factor shared by $f(x)$’s numerator and denominator, there is a hole at $x = 4$. Find the $y$-coordinate by substituting $x=4$ into the simplified form of $f(x)$.

$\begin{aligned}f(x)&= \dfrac{\cancel{x – 4}}{(x -2)\cancel{(x – 4)}}\\&= \dfrac{1}{x -2}\\\\f(4)&= \dfrac{1}{4 -2}\\&= \dfrac{1}{2}\end{aligned}$

From the simplified form of $f(x)$, $\dfrac{1}{x – 2}$, we can see that $f(x)$ will also have a vertical asymptote at $x = 2$.

d. This means that $f(x)$ is not continuous and $x = 4$ is a removable discontinuity while $x =2$ is an infinite discontinuity.

Example 5

Given that the function, $ f(x)=\left\{\begin{matrix}Mx + N,&x\leq -1\\ 3x^2 – 5Mx -N,&-1<x\leq 1\\-6,&x> 1\end{matrix}\right.$, is continuous for all values of $x$, find the values of $M$ and $N$.

Solution

Let’s inspect the continuity of $f(x)$ in each of the piecewise function’s components.

• When $x \leq -1$, $f(x) = Mx +N$, and since this is a polynomial function, we can say that $Mx + N$ will always be continuous regardless of $M$ and $N$’s values.
• The same reasoning applies when $f(x) = 3x^2 – 5x – N$ and $f(x) = -6$ for the intervals, $-1<x\leq 1$ and $ x> -1$, respectively.

To make sure that $f(x)$ is continuous throughout, we’ll need to inspect how it behaves at $x = -1$ and $x = 1$.

Starting with the first condition of continuous functions, $f(-1)$ and $f(1)$ must be defined.

This means that $f(-1) = N -M $ and $f(1) = 3 – 5M – N $ must be defined for $f(x)$ to be continuous.

Let’s evaluate the one-sided limits of $f(x)$ as $x$ approaches both $1$ and $-1$. Starting with $\lim_{x \rightarrow -1^{-}} f(x)$ and $\lim_{x \rightarrow -1^{+}} f(x)$:

For the limit of $f(x)$ to exist and be defined, both one-sided limits must be equal to each other. Equate the two one-sided limits’ expressions to each other.

$\begin{aligned}\lim_{x \rightarrow -1^{-}} f(x) &= \lim_{x \rightarrow -1^{+}} f(x) \\N -M &=3 + 5M -N\\2N – 6M &= 3\end{aligned}$

We apply the same process to observe the one-sided limits of $f(x)$ as it approaches $x = 1$.

Equating the two limits, we have the equation shown below.

$\begin{aligned}\lim_{x \rightarrow 1^{-}} f(x) &= \lim_{x \rightarrow 1^{+}} f(x)\\3 – 5M – N &= -6\\-5M – N &= -9\\ 5M + N&=9\end{aligned}$

This means that $M$ and $N$ must satisfy the simultaneous equations, $2N – 6M = 3$ and $5M + N = 9$. Let’s apply what we’ve in learned in solving systems of linear equations to find $M$ and $N$.

• Isolate $N$ from the second equation.
• Substitute this expression into the first equation to solve for $M$.
• Use the value of $M$ to find $N$.

$\begin{aligned}5M + N &= 9\\N&= 9- 5M\\\\2N – 6M &= 3\\2(9 – 5M) – 6M &= 3\\18 – 10M- 6M&=3\\18 – 16M &= 3\\-16M &= -15\\ M&= \dfrac{15}{16}\end{aligned}$

Using $M = \dfrac{15}{16}$, we can now find $N$ using $N = 9-5M$.

$\begin{aligned}N&= 9- 5\left(\dfrac{15}{16}\right)\\&=9 – \dfrac{75}{16}\\&= \dfrac{69}{16}\end{aligned}$

This means that for $f(x)$ to be continuous, we need $M$ and $N$, to be equal to $\dfrac{15}{16}$ and $\dfrac{69}{16}$, respectively.